Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-27T00:08:14.023Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit transition between hypergeometric functions of type BC and type A

Part of: Abstract harmonic analysis Global differential geometry

Published online by Cambridge University Press:  19 June 2013

Margit Rösler ,
Tom Koornwinder  and
Michael Voit
Margit Rösler
Affiliation:
Institut für Mathematik, Universität Paderborn, Warburger Str. 100, D-33098 Paderborn, Germany email roesler@math.upb.de
Tom Koornwinder
Affiliation:
Korteweg de Vries Institute, University of Amsterdam, P.O. Box 94248, 1090 CE Amsterdam, The Netherlands email T.H.Koornwinder@uva.nl
Michael Voit
Affiliation:
Fakultät Mathematik, Technische Universität Dortmund, Vogelpothsweg 87, D-44221 Dortmund, Germany email michael.voit@math.tu-dortmund.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 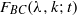${F}_{BC} (\lambda , k; t)$ be the Heckman–Opdam hypergeometric function of type BC with multiplicities 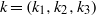$k= ({k}_{1} , {k}_{2} , {k}_{3} )$ and weighted half-sum 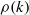$\rho (k)$ of positive roots. We prove that 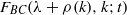${F}_{BC} (\lambda + \rho (k), k; t)$ converges as 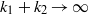${k}_{1} + {k}_{2} \rightarrow \infty $ and 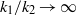${k}_{1} / {k}_{2} \rightarrow \infty $ to a function of type A for 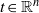$t\in { \mathbb{R} }^{n} $ and 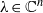$\lambda \in { \mathbb{C} }^{n} $. This limit is obtained from a corresponding result for Jacobi polynomials of type BC, which is proven for a slightly more general limit behavior of the multiplicities, using an explicit representation of Jacobi polynomials in terms of Jack polynomials. Our limits include limit transitions for the spherical functions of non-compact Grassmann manifolds over one of the fields 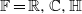$ \mathbb{F} = \mathbb{R} , \mathbb{C} , \mathbb{H} $ when the rank is fixed and the dimension tends to infinity. The limit functions turn out to be exactly the spherical functions of the corresponding infinite-dimensional Grassmann manifold in the sense of Olshanski.

Keywords

hypergeometric functions associated with root systemslimit transitionsHeckman–Opdam theoryspherical functionsGrassmann manifoldsOlshanski spherical pairs

MSC classification

Secondary: 33C67: Hypergeometric functions associated with root systems 33C52: Orthogonal polynomials and functions associated with root systems 43A90: Spherical functions 33C80: Connections with groups and algebras, and related topics 53C35: Symmetric spaces
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 8 , August 2013 , pp. 1381 - 1400
Copyright
© The Author(s) 2013 

References

Baker, T. and Forrester, P., The Calogero-Sutherland model and generalized classical polynomials, Comm. Math. Phys. 188 (1997), 175–216.CrossRefGoogle Scholar
Beerends, R. J. and Opdam, E. M., Certain hypergeometric series related to the root system BC, Trans. Amer. Math. Soc. 339 (1993), 581–609.Google Scholar
Dawson, M., Olafsson, G. and Wolf, J. A., Direct systems of spherical functions and representations, J. Lie Theory 23 (2013), 711–729.Google Scholar
Faraut, J., Infinite dimensional spherical analysis, COE Lecture Notes, vol. 10 (Kyushu University, Fukuoka, 2008).Google Scholar
Gunning, R. C., Introduction to holomorphic functions of several variables. Volume 1: Function theory (Brooks/Cole, Belmont, CA, 1990).Google Scholar
Hallnäs, M., Multivariable Bessel polynomials related to the hyperbolic Sutherland model with external Morse potential, Int. Math. Res. Not. 9 (2009), 1573–1611.Google Scholar
Heckman, G., Root systems and hypergeometric functions II, Compositio Math. 64 (1987), 353–373.Google Scholar
Heckman, G. J., An elementary approach to the hypergeometric shift operators of Opdam, Invent. Math. 103 (1991), 341–350.Google Scholar
Heckman, G., Dunkl operators, Astérisque 245 (1997), 223–246; Séminaire N. Bourbaki, 1996/97, exp. no. 828.Google Scholar
Heckman, G. and Schlichtkrull, H., Harmonic analysis and special functions on symmetric spaces, Perspectives in Mathematics, vol. 16 (Academic Press, San Diego, 1994).Google Scholar
Koornwinder, T., Jacobi functions and analysis on noncompact semisimple Lie groups, in Special functions: group theoretical aspects and applications, eds Askey, R., Koornwinder, T. and Schempp, W. (Reidel, Dordrecht, 1984), 1–85.Google Scholar
Koornwinder, T., Jacobi polynomials of type BC, Jack polynomials, limit transitions and $O(\infty )$, in Mathematical analysis, wavelets, and signal processing, Contemporary Mathematics, vol. 190 (American Mathematical Society, Providence, RI, 1995), 283–286; arXiv:math/9307216.CrossRefGoogle Scholar
Lassalle, M., Polynômes de Jacobi généralisés, C. R. Acad. Sci. Paris Sér. I Math. 312 (1991), 425–428.Google Scholar
Macdonald, I. G., Hypergeometric functions I, Unpublished manuscript.Google Scholar
Macdonald, I. G., Orthogonal polynomials associated with root systems, Sém. Lothar. Combin. 45 (2000), Article B45a.Google Scholar
Olshanskii, G. I., Infinite-dimensional classical groups of finite $r$-rank: Description of representations and asymptotic theory, Funct. Anal. Appl. 18 (1984), 22–34.Google Scholar
Olshanskii, G. I., Unitary representations of infinite-dimensional pairs $(G, K)$ and the formalism of R. Howe, in Representations of Lie groups and related topics, Advanced Studies in Contemporary Mathematics, vol. 7, eds Vershik, A. and Zhelobenko, D. (Gordon and Breach, Amsterdam, 1990).Google Scholar
Opdam, E. M., Harmonic analysis for certain representations of graded Hecke algebras, Acta Math. 175 (1995), 75–121.Google Scholar
Opdam, E. M., Lecture notes on Dunkl operators for real and complex reflection groups, MSJ Memoirs, vol. 8 (Mathematical Society of Japan, Tokyo, 2000).Google Scholar
Rösler, M., Positive convolution structure for a class of Heckman–Opdam hypergeometric functions of type $BC$, J. Funct. Anal. 258 (2010), 2779–2800.Google Scholar
Rösler, M. and Voit, M., A limit relation for Dunkl–Bessel functions of type A and B, Symmetry Integrability Geom. Methods Appl. (SIGMA) 4 (2008), Article 083.Google Scholar
Rösler, M. and Voit, M., Olshanski spherical functions for infinite-dimensional motion groups of fixed rank, J. Lie Theory (2013), 899–920.Google Scholar
Schapira, B., Contributions to the hypergeometric function theory of Heckman and Opdam: sharp estimates, Schwartz space, heat kernel, Geom. Funct. Anal. 18 (2008), 222–250.Google Scholar
Stanley, R. P., Some combinatorial properties of Jack symmetric functions, Adv. Math. 77 (1989), 76–115.Google Scholar
Stokman, J. and Koornwinder, T., Limit transitions for BC type multivariable orthogonal polynomials, Canad. J. Math. 490 (1997), 373–404.Google Scholar
Titchmarsh, E. C., The theory of functions, second edition (Oxford University Press, London, 1939).Google Scholar
van Diejen, J. F., Commuting difference operators with polynomial eigenfunctions, Compositio Math. 95 (1995), 183–233.Google Scholar