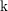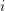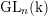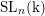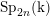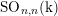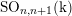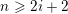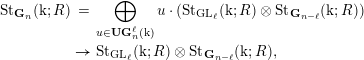1 Introduction
Let
![]() $\mathbf{G}$
be a connected reductive group over a field
$\mathbf{G}$
be a connected reductive group over a field
![]() $\text{k}$
. A basic geometric object associated to
$\text{k}$
. A basic geometric object associated to
![]() $\mathbf{G}(\text{k})$
is its Tits building. By definition, this is the simplicial complex
$\mathbf{G}(\text{k})$
is its Tits building. By definition, this is the simplicial complex
![]() ${\mathcal{T}}_{\mathbf{G}}(\text{k})$
whose
${\mathcal{T}}_{\mathbf{G}}(\text{k})$
whose
![]() $i$
-simplices are increasing sequences
$i$
-simplices are increasing sequences
of parabolic
![]() $\text{k}$
-subgroups of
$\text{k}$
-subgroups of
![]() $\mathbf{G}(\text{k})$
. Letting
$\mathbf{G}(\text{k})$
. Letting
![]() $r$
be the semisimple
$r$
be the semisimple
![]() $\text{k}$
-rank of
$\text{k}$
-rank of
![]() $\mathbf{G}$
, the complex
$\mathbf{G}$
, the complex
![]() ${\mathcal{T}}_{\mathbf{G}}(\text{k})$
is
${\mathcal{T}}_{\mathbf{G}}(\text{k})$
is
![]() $(r-1)$
-dimensional, and the Solomon–Tits theorem [Reference BrownBro89, Theorem IV.5.2] says that in fact
$(r-1)$
-dimensional, and the Solomon–Tits theorem [Reference BrownBro89, Theorem IV.5.2] says that in fact
![]() ${\mathcal{T}}_{\mathbf{G}}(\text{k})$
is homotopy equivalent to a wedge of
${\mathcal{T}}_{\mathbf{G}}(\text{k})$
is homotopy equivalent to a wedge of
![]() $(r-1)$
-dimensional spheres. Letting
$(r-1)$
-dimensional spheres. Letting
![]() $R$
be a commutative ring, the Steinberg representation of
$R$
be a commutative ring, the Steinberg representation of
![]() $\mathbf{G}(\text{k})$
over
$\mathbf{G}(\text{k})$
over
![]() $R$
, denoted
$R$
, denoted
![]() $\operatorname{St}_{\mathbf{G}}(\text{k};R)$
, is
$\operatorname{St}_{\mathbf{G}}(\text{k};R)$
, is
![]() $\widetilde{\operatorname{H}}_{r-1}({\mathcal{T}}_{\mathbf{G}}(\text{k});R)$
. This is one of the most important representations of
$\widetilde{\operatorname{H}}_{r-1}({\mathcal{T}}_{\mathbf{G}}(\text{k});R)$
. This is one of the most important representations of
![]() $\mathbf{G}(\text{k})$
; for instance, if
$\mathbf{G}(\text{k})$
; for instance, if
![]() $\mathbf{G}$
is any of the classical groups in Theorem 1.1 below (e.g.
$\mathbf{G}$
is any of the classical groups in Theorem 1.1 below (e.g.
![]() $\mathbf{G}=\operatorname{SL}_{n}$
) and
$\mathbf{G}=\operatorname{SL}_{n}$
) and
![]() $\text{k}$
is a finite field of characteristic
$\text{k}$
is a finite field of characteristic
![]() $p$
, then
$p$
, then
![]() $\operatorname{St}_{\mathbf{G}}(\text{k};\mathbb{C})$
is the unique irreducible representation of
$\operatorname{St}_{\mathbf{G}}(\text{k};\mathbb{C})$
is the unique irreducible representation of
![]() $\mathbf{G}(\text{k})$
whose dimension is a positive power of
$\mathbf{G}(\text{k})$
whose dimension is a positive power of
![]() $p$
(see [Reference Malle and ZalesskiĭMZ01], which proves this aside from three small cases that must be checked by hand). See [Reference HumphreysHum87] for a survey of many results concerning the Steinberg representation.
$p$
(see [Reference Malle and ZalesskiĭMZ01], which proves this aside from three small cases that must be checked by hand). See [Reference HumphreysHum87] for a survey of many results concerning the Steinberg representation.
The twisted homology groups
![]() $\operatorname{H}_{i}(\mathbf{G}(\text{k});\operatorname{St}_{\mathbf{G}}(\text{k};R))$
play an interesting role in algebraic K-theory; see [Reference QuillenQui72, Theorem 3]. If
$\operatorname{H}_{i}(\mathbf{G}(\text{k});\operatorname{St}_{\mathbf{G}}(\text{k};R))$
play an interesting role in algebraic K-theory; see [Reference QuillenQui72, Theorem 3]. If
![]() $\mathbf{G}(\text{k})$
is a finite group of Lie type, then
$\mathbf{G}(\text{k})$
is a finite group of Lie type, then
![]() $\operatorname{St}_{\mathbf{G}}(\text{k};\text{k})$
is a projective
$\operatorname{St}_{\mathbf{G}}(\text{k};\text{k})$
is a projective
![]() $\mathbf{G}(\text{k})$
-module (see [Reference HumphreysHum87]), and thus the homology groups
$\mathbf{G}(\text{k})$
-module (see [Reference HumphreysHum87]), and thus the homology groups
![]() $\operatorname{H}_{i}(\mathbf{G}(\text{k});\operatorname{St}_{\mathbf{G}}(\text{k};\text{k}))$
all vanish. However, it is definitely not the case that
$\operatorname{H}_{i}(\mathbf{G}(\text{k});\operatorname{St}_{\mathbf{G}}(\text{k};\text{k}))$
all vanish. However, it is definitely not the case that
![]() $\operatorname{St}_{\mathbf{G}}(\text{k};R)$
is projective for a general commutative ring
$\operatorname{St}_{\mathbf{G}}(\text{k};R)$
is projective for a general commutative ring
![]() $R$
, and if
$R$
, and if
![]() $\text{k}$
is an infinite field then
$\text{k}$
is an infinite field then
![]() $\operatorname{St}_{\mathbf{G}}(\text{k};\text{k})$
need not be projective. Our main theorem says that, nevertheless, for the classical groups, the homology groups
$\operatorname{St}_{\mathbf{G}}(\text{k};\text{k})$
need not be projective. Our main theorem says that, nevertheless, for the classical groups, the homology groups
![]() $\operatorname{H}_{i}(\mathbf{G}(\text{k});\operatorname{St}_{\mathbf{G}}(\text{k};R))$
always vanish in a stable range.
$\operatorname{H}_{i}(\mathbf{G}(\text{k});\operatorname{St}_{\mathbf{G}}(\text{k};R))$
always vanish in a stable range.
Theorem 1.1. Let
![]() $\mathbf{G}_{n}$
be either
$\mathbf{G}_{n}$
be either
![]() $\operatorname{GL}_{n}$
,
$\operatorname{GL}_{n}$
,
![]() $\operatorname{SL}_{n}$
,
$\operatorname{SL}_{n}$
,
![]() $\operatorname{Sp}_{2n}$
,
$\operatorname{Sp}_{2n}$
,
![]() $\operatorname{SO}_{n,n}$
, or
$\operatorname{SO}_{n,n}$
, or
![]() $\operatorname{SO}_{n,n+1}$
. Then for all fields
$\operatorname{SO}_{n,n+1}$
. Then for all fields
![]() $\text{k}$
and all commutative rings
$\text{k}$
and all commutative rings
![]() $R$
, we have
$R$
, we have
![]() $\operatorname{H}_{i}(\mathbf{G}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))=0$
for
$\operatorname{H}_{i}(\mathbf{G}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))=0$
for
![]() $n\geqslant 2i+2$
. Furthermore, there exists a surjection
$n\geqslant 2i+2$
. Furthermore, there exists a surjection
![]() $\operatorname{H}_{i}(\mathbf{G}_{2i}(\text{k});\operatorname{St}_{\mathbf{G}_{2i}}(\text{k};R))\rightarrow \operatorname{H}_{i}(\mathbf{G}_{2i+1}(\text{k});\operatorname{St}_{\mathbf{G}_{2i+1}}(\text{k};R))$
.
$\operatorname{H}_{i}(\mathbf{G}_{2i}(\text{k});\operatorname{St}_{\mathbf{G}_{2i}}(\text{k};R))\rightarrow \operatorname{H}_{i}(\mathbf{G}_{2i+1}(\text{k});\operatorname{St}_{\mathbf{G}_{2i+1}}(\text{k};R))$
.
Remark 1.2. When
![]() $\text{char}(\text{k})=2$
, the groups
$\text{char}(\text{k})=2$
, the groups
![]() $\operatorname{SO}_{n,n}(\text{k})$
and
$\operatorname{SO}_{n,n}(\text{k})$
and
![]() $\operatorname{SO}_{n,n+1}(\text{k})$
in Theorem 1.1 are to be taken naively as the stabilizers of appropriate quadratic forms (see § 2.1 below); we ignore the Dickson invariant.
$\operatorname{SO}_{n,n+1}(\text{k})$
in Theorem 1.1 are to be taken naively as the stabilizers of appropriate quadratic forms (see § 2.1 below); we ignore the Dickson invariant.
Theorem 1.1 (and its proof) is motivated by the following conjecture of Church, Farb and Putman [Reference Church, Farb and PutmanCFP14]. Recall that Borel and Serre [Reference Borel and SerreBS73] proved that the virtual cohomological dimension of
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
is
$\operatorname{SL}_{n}(\mathbb{Z})$
is
![]() $\binom{n}{2}$
.
$\binom{n}{2}$
.
Conjecture 1.3 [Reference Church, Farb and PutmanCFP14, Conjecture 2].
We have
![]() $\operatorname{H}^{\binom{n}{2}-i}(\operatorname{SL}_{n}(\mathbb{Z});\mathbb{Q})=0$
for
$\operatorname{H}^{\binom{n}{2}-i}(\operatorname{SL}_{n}(\mathbb{Z});\mathbb{Q})=0$
for
![]() $n\geqslant i+2$
.
$n\geqslant i+2$
.
In other words, the rational cohomology of
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
vanishes in codimension
$\operatorname{SL}_{n}(\mathbb{Z})$
vanishes in codimension
![]() $i$
as long as
$i$
as long as
![]() $n$
is sufficiently large. Conjecture 1.3 was proved for
$n$
is sufficiently large. Conjecture 1.3 was proved for
![]() $i=0$
by Lee and Szczarba [Reference Lee and SzczarbaLS76] and for
$i=0$
by Lee and Szczarba [Reference Lee and SzczarbaLS76] and for
![]() $i=1$
by Church and Putman [Reference Church and PutmanCP17]. It is open for
$i=1$
by Church and Putman [Reference Church and PutmanCP17]. It is open for
![]() $i\geqslant 2$
.
$i\geqslant 2$
.
To connect Conjecture 1.3 to Theorem 1.1, recall that Borel and Serre [Reference Borel and SerreBS73] proved that
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
satisfies a version of Poincaré–Lefschetz duality called virtual Bieri–Eckmann duality. This duality involves a ‘dualizing module’ that measures the ‘homology at infinity’. In our situation, that dualizing module is the Steinberg representation
$\operatorname{SL}_{n}(\mathbb{Z})$
satisfies a version of Poincaré–Lefschetz duality called virtual Bieri–Eckmann duality. This duality involves a ‘dualizing module’ that measures the ‘homology at infinity’. In our situation, that dualizing module is the Steinberg representation
![]() $\operatorname{St}_{\operatorname{SL}_{n}}(\mathbb{Q};\mathbb{Q})$
and we have
$\operatorname{St}_{\operatorname{SL}_{n}}(\mathbb{Q};\mathbb{Q})$
and we have
Conjecture 1.3 is thus equivalent to the following conjecture, which resembles Theorem 1.1 for
![]() $\mathbf{G}_{n}=\operatorname{SL}_{n}$
.
$\mathbf{G}_{n}=\operatorname{SL}_{n}$
.
Conjecture 1.4. We have
![]() $\operatorname{H}_{i}(\operatorname{SL}_{n}(\mathbb{Z});\operatorname{St}_{\operatorname{SL}_{n}}(\mathbb{Q};\mathbb{Q}))=0$
for
$\operatorname{H}_{i}(\operatorname{SL}_{n}(\mathbb{Z});\operatorname{St}_{\operatorname{SL}_{n}}(\mathbb{Q};\mathbb{Q}))=0$
for
![]() $n\geqslant i+2$
.
$n\geqslant i+2$
.
Remark 1.5. The proofs by Lee and Szczarba [Reference Lee and SzczarbaLS76] and Church and Putman [Reference Church and PutmanCP17] of special cases of Conjecture 1.3 both start by translating things into the language of Conjecture 1.4.
We now briefly describe our proof of Theorem 1.1. As we will discuss in § 3 below, there is a natural inclusion
![]() $\operatorname{St}_{\mathbf{G}_{n-1}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
. This induces a stabilization map
$\operatorname{St}_{\mathbf{G}_{n-1}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
. This induces a stabilization map
We will show in § 3 that to prove that
![]() $\operatorname{H}_{i}(\mathbf{G}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))=0$
for large
$\operatorname{H}_{i}(\mathbf{G}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))=0$
for large
![]() $n$
, it is enough to prove the seemingly weaker assertion that (1.1) is a surjection for large
$n$
, it is enough to prove the seemingly weaker assertion that (1.1) is a surjection for large
![]() $n$
. This idea was first introduced by Church, Farb and Putman [Reference Church, Farb and PutmanCFP14] as a strategy for proving Conjecture 1.4. It was also noticed by Ash in unpublished work.
$n$
. This idea was first introduced by Church, Farb and Putman [Reference Church, Farb and PutmanCFP14] as a strategy for proving Conjecture 1.4. It was also noticed by Ash in unpublished work.
The surjectivity of (1.1) is a weak form of homological stability. There is an enormous literature on homological stability theorems. The basic technique underlying most results in the subject goes back to unpublished work of Quillen. In [Reference DwyerDwy80], Dwyer used these ideas to prove a twisted homological stability theorem for
![]() $\operatorname{GL}_{n}(\text{k})$
with quite general coefficient systems. This work was later generalized by van der Kallen [Reference van der KallenvdK80] and very recently by Randal-Williams and Wahl [Reference Randal-Williams and WahlRW15], whose results cover all the classical groups in Theorem 1.1. Unfortunately, the Steinberg representation does not satisfy the conditions in any of these known theorems. Indeed, these theorems are general enough that if it did, then this would quickly lead to a proof of Conjecture 1.4. Nevertheless, we are able to use some delicate properties of the Steinberg representation to jury-rig the Quillen machine such that it works to prove that (1.1) is surjective for large
$\operatorname{GL}_{n}(\text{k})$
with quite general coefficient systems. This work was later generalized by van der Kallen [Reference van der KallenvdK80] and very recently by Randal-Williams and Wahl [Reference Randal-Williams and WahlRW15], whose results cover all the classical groups in Theorem 1.1. Unfortunately, the Steinberg representation does not satisfy the conditions in any of these known theorems. Indeed, these theorems are general enough that if it did, then this would quickly lead to a proof of Conjecture 1.4. Nevertheless, we are able to use some delicate properties of the Steinberg representation to jury-rig the Quillen machine such that it works to prove that (1.1) is surjective for large
![]() $n$
.
$n$
.
Remark 1.6. Homological stability for a sequence of groups and homomorphisms
![]() $X_{1}\rightarrow X_{2}\rightarrow \cdots \,$
states that the induced maps
$X_{1}\rightarrow X_{2}\rightarrow \cdots \,$
states that the induced maps
![]() $\operatorname{H}_{i}(X_{n})\rightarrow \operatorname{H}_{i}(X_{n+1})$
are isomorphisms for
$\operatorname{H}_{i}(X_{n})\rightarrow \operatorname{H}_{i}(X_{n+1})$
are isomorphisms for
![]() $n\gg 0$
. Alternatively, we can think of each map as ‘multiplication by
$n\gg 0$
. Alternatively, we can think of each map as ‘multiplication by
![]() $t$
’ and give
$t$
’ and give
![]() $\bigoplus _{n}\operatorname{H}_{i}(X_{n})$
the structure of a
$\bigoplus _{n}\operatorname{H}_{i}(X_{n})$
the structure of a
![]() $R[t]$
-module, where
$R[t]$
-module, where
![]() $R$
denotes our coefficient ring. At least when
$R$
denotes our coefficient ring. At least when
![]() $R$
is a field, this isomorphism would be a consequence of finite generation.
$R$
is a field, this isomorphism would be a consequence of finite generation.
In our setting, with homology twisted by the Steinberg representation, one should instead think of this map as ‘multiplication by
![]() $t$
’ where
$t$
’ where
![]() $t$
is a generator for the exterior algebra in one variable
$t$
is a generator for the exterior algebra in one variable
![]() $R[t]/t^{2}$
, so that the groups
$R[t]/t^{2}$
, so that the groups
![]() $\operatorname{H}_{i}$
being
$\operatorname{H}_{i}$
being
![]() $0$
for
$0$
for
![]() $n\gg 0$
would again be a consequence of finite generation. At least when
$n\gg 0$
would again be a consequence of finite generation. At least when
![]() $\text{k}$
is a finite field of size
$\text{k}$
is a finite field of size
![]() $q$
and
$q$
and
![]() $R$
is the field of complex numbers, this is consistent with the idea that
$R$
is the field of complex numbers, this is consistent with the idea that
![]() $\operatorname{GL}_{n}(\mathbf{F}_{q})$
is a
$\operatorname{GL}_{n}(\mathbf{F}_{q})$
is a
![]() $q$
-analogue of the symmetric group and the Steinberg representation is the
$q$
-analogue of the symmetric group and the Steinberg representation is the
![]() $q$
-analogue of its sign representation, which is made more precise via their connection to symmetric functions, see [Reference MacdonaldMac95, §§ I.7, IV.4].
$q$
-analogue of its sign representation, which is made more precise via their connection to symmetric functions, see [Reference MacdonaldMac95, §§ I.7, IV.4].
Outline. We begin in § 2 with some background and notation. Next, in § 3 we reduce Theorem 1.1 to an appropriate homological stability theorem. We then prove a key isomorphism in § 4. We prove Theorem 1.1 in § 5. This proof depends on a calculation which we perform in § 6.
Convention regarding the empty set. If
![]() $X$
is the empty set and
$X$
is the empty set and
![]() $R$
is a commutative ring, then we define
$R$
is a commutative ring, then we define
![]() $\widetilde{\operatorname{H}}_{-1}(X;R)=R$
. With this convention, if the semisimple
$\widetilde{\operatorname{H}}_{-1}(X;R)=R$
. With this convention, if the semisimple
![]() $\text{k}$
-rank of
$\text{k}$
-rank of
![]() $\mathbf{G}$
is
$\mathbf{G}$
is
![]() $0$
, then
$0$
, then
![]() $\operatorname{St}_{\mathbf{G}}(\text{k};R)=R$
with the trivial
$\operatorname{St}_{\mathbf{G}}(\text{k};R)=R$
with the trivial
![]() $\mathbf{G}(\text{k})$
-action.
$\mathbf{G}(\text{k})$
-action.
2 Background and notation
This section contains some background information and notation needed in the remainder of the paper. It consists of two subsections: § 2.1 introduces some distinguished parabolic subgroups, and § 2.2 gives some background about the Steinberg representations.
Throughout this section,
![]() $\text{k}$
is a field and
$\text{k}$
is a field and
![]() $\mathbf{G}_{n}$
is either
$\mathbf{G}_{n}$
is either
![]() $\operatorname{GL}_{n}$
,
$\operatorname{GL}_{n}$
,
![]() $\operatorname{SL}_{n}$
,
$\operatorname{SL}_{n}$
,
![]() $\operatorname{Sp}_{2n}$
,
$\operatorname{Sp}_{2n}$
,
![]() $\operatorname{SO}_{n,n}$
, or
$\operatorname{SO}_{n,n}$
, or
![]() $\operatorname{SO}_{n,n+1}$
.
$\operatorname{SO}_{n,n+1}$
.
2.1 Parabolic and stabilizer subgroups
Our proof of Theorem 1.1 depends on a careful study of various subgroups of
![]() $\mathbf{G}_{n}(\text{k})$
. In this section, we will introduce notation for these subgroups: a certain parabolic subgroup
$\mathbf{G}_{n}(\text{k})$
. In this section, we will introduce notation for these subgroups: a certain parabolic subgroup
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
, its unipotent radical
$\mathbf{PG}_{n}^{\ell }(\text{k})$
, its unipotent radical
![]() $\mathbf{UG}_{n}^{\ell }(\text{k})$
, a Levi component
$\mathbf{UG}_{n}^{\ell }(\text{k})$
, a Levi component
![]() $\mathbf{LG}_{n}^{\ell }(\text{k})$
of
$\mathbf{LG}_{n}^{\ell }(\text{k})$
of
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
, and another subgroup
$\mathbf{PG}_{n}^{\ell }(\text{k})$
, and another subgroup
![]() $\mathbf{FG}_{n}^{\ell }(\text{k})$
that lies in
$\mathbf{FG}_{n}^{\ell }(\text{k})$
that lies in
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
and fixes certain vectors.
$\mathbf{PG}_{n}^{\ell }(\text{k})$
and fixes certain vectors.
General and special linear groups
Assume first that
![]() $\mathbf{G}_{n}$
is either
$\mathbf{G}_{n}$
is either
![]() $\operatorname{GL}_{n}$
or
$\operatorname{GL}_{n}$
or
![]() $\operatorname{SL}_{n}$
. The group
$\operatorname{SL}_{n}$
. The group
![]() $\mathbf{G}_{n}(\text{k})$
thus acts on the vector space
$\mathbf{G}_{n}(\text{k})$
thus acts on the vector space
![]() $\text{k}^{n}$
, and the
$\text{k}^{n}$
, and the
![]() $\text{k}$
-parabolic subgroups of
$\text{k}$
-parabolic subgroups of
![]() $\mathbf{G}_{n}(\text{k})$
are the stabilizers of flags of subspaces of
$\mathbf{G}_{n}(\text{k})$
are the stabilizers of flags of subspaces of
![]() $\text{k}^{n}$
. Let
$\text{k}^{n}$
. Let
![]() $(\vec{a}_{1},\ldots ,\vec{a}_{n})$
be the standard basis for
$(\vec{a}_{1},\ldots ,\vec{a}_{n})$
be the standard basis for
![]() $\text{k}^{n}$
. For
$\text{k}^{n}$
. For
![]() $1\leqslant \ell \leqslant n$
, the group
$1\leqslant \ell \leqslant n$
, the group
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
is defined to be the
$\mathbf{PG}_{n}^{\ell }(\text{k})$
is defined to be the
![]() $\mathbf{G}_{n}(\text{k})$
-stabilizer of the flag
$\mathbf{G}_{n}(\text{k})$
-stabilizer of the flag
The group
![]() $\mathbf{UG}_{n}^{\ell }(\text{k})$
is the subgroup of
$\mathbf{UG}_{n}^{\ell }(\text{k})$
is the subgroup of
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
consisting of all
$\mathbf{PG}_{n}^{\ell }(\text{k})$
consisting of all
![]() $M\in \mathbf{PG}_{n}^{\ell }(\text{k})$
that act as the identity on both
$M\in \mathbf{PG}_{n}^{\ell }(\text{k})$
that act as the identity on both
The group
![]() $\mathbf{LG}_{n}^{\ell }(\text{k})$
is defined to be the
$\mathbf{LG}_{n}^{\ell }(\text{k})$
is defined to be the
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
-stabilizer of the flag
$\mathbf{PG}_{n}^{\ell }(\text{k})$
-stabilizer of the flag
If
![]() $\mathbf{G}_{n}=\operatorname{GL}_{n}$
then
$\mathbf{G}_{n}=\operatorname{GL}_{n}$
then
![]() $\mathbf{LG}_{n}^{\ell }(\text{k})$
is the subgroup
$\mathbf{LG}_{n}^{\ell }(\text{k})$
is the subgroup
![]() $\operatorname{GL}_{\ell }(\text{k})\times \operatorname{GL}_{n-\ell }(\text{k})$
of
$\operatorname{GL}_{\ell }(\text{k})\times \operatorname{GL}_{n-\ell }(\text{k})$
of
![]() $\mathbf{G}_{n}$
, while if
$\mathbf{G}_{n}$
, while if
![]() $\mathbf{G}_{n}=\operatorname{SL}_{n}$
then
$\mathbf{G}_{n}=\operatorname{SL}_{n}$
then
![]() $\mathbf{LG}_{n}^{\ell }(\text{k})$
is the subgroup of
$\mathbf{LG}_{n}^{\ell }(\text{k})$
is the subgroup of
![]() $\operatorname{GL}_{\ell }(\text{k})\times \operatorname{GL}_{n-\ell }(\text{k})$
consisting of matrices of determinant
$\operatorname{GL}_{\ell }(\text{k})\times \operatorname{GL}_{n-\ell }(\text{k})$
consisting of matrices of determinant
![]() $1$
. Finally, define
$1$
. Finally, define
We thus have
![]() $\mathbf{FG}_{n}^{\ell }(\text{k})\subset \mathbf{PG}_{n}^{\ell }(\text{k})$
.
$\mathbf{FG}_{n}^{\ell }(\text{k})\subset \mathbf{PG}_{n}^{\ell }(\text{k})$
.
Symplectic groups
Now assume that
![]() $\mathbf{G}_{n}=\operatorname{Sp}_{2n}$
. Letting
$\mathbf{G}_{n}=\operatorname{Sp}_{2n}$
. Letting
![]() $\unicode[STIX]{x1D714}(\cdot ,\cdot )$
be the standard symplectic form on
$\unicode[STIX]{x1D714}(\cdot ,\cdot )$
be the standard symplectic form on
![]() $\text{k}^{2n}$
, the group
$\text{k}^{2n}$
, the group
![]() $\mathbf{G}_{n}(\text{k})$
is the subgroup of
$\mathbf{G}_{n}(\text{k})$
is the subgroup of
![]() $\operatorname{GL}_{n}(\text{k})$
consisting of elements that preserve
$\operatorname{GL}_{n}(\text{k})$
consisting of elements that preserve
![]() $\unicode[STIX]{x1D714}(\cdot ,\cdot )$
. The
$\unicode[STIX]{x1D714}(\cdot ,\cdot )$
. The
![]() $\text{k}$
-parabolic subgroups of
$\text{k}$
-parabolic subgroups of
![]() $\mathbf{G}_{n}(\text{k})$
are the
$\mathbf{G}_{n}(\text{k})$
are the
![]() $\mathbf{G}_{n}(\text{k})$
-stabilizers of flags of isotropic subspaces of
$\mathbf{G}_{n}(\text{k})$
-stabilizers of flags of isotropic subspaces of
![]() $\text{k}^{2n}$
, that is, subspaces on which
$\text{k}^{2n}$
, that is, subspaces on which
![]() $\unicode[STIX]{x1D714}(\cdot ,\cdot )$
vanishes identically. Let
$\unicode[STIX]{x1D714}(\cdot ,\cdot )$
vanishes identically. Let
![]() $(\vec{a}_{1},\ldots ,\vec{a}_{n},\vec{b}_{1},\ldots ,\vec{b}_{n})$
be the standard symplectic basis for
$(\vec{a}_{1},\ldots ,\vec{a}_{n},\vec{b}_{1},\ldots ,\vec{b}_{n})$
be the standard symplectic basis for
![]() $\text{k}^{2n}$
, so
$\text{k}^{2n}$
, so
for
![]() $1\leqslant j,j^{\prime }\leqslant n$
, where
$1\leqslant j,j^{\prime }\leqslant n$
, where
![]() $\unicode[STIX]{x1D6FF}_{jj^{\prime }}$
is the Kronecker delta function. For
$\unicode[STIX]{x1D6FF}_{jj^{\prime }}$
is the Kronecker delta function. For
![]() $1\leqslant \ell \leqslant n$
, the group
$1\leqslant \ell \leqslant n$
, the group
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
is defined to be the
$\mathbf{PG}_{n}^{\ell }(\text{k})$
is defined to be the
![]() $\mathbf{G}_{n}(\text{k})$
-stabilizer of the isotropic flag
$\mathbf{G}_{n}(\text{k})$
-stabilizer of the isotropic flag
The group
![]() $\mathbf{UG}_{n}^{\ell }(\text{k})$
is the subgroup of
$\mathbf{UG}_{n}^{\ell }(\text{k})$
is the subgroup of
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
consisting of all
$\mathbf{PG}_{n}^{\ell }(\text{k})$
consisting of all
![]() $M\in \mathbf{PG}_{n}^{\ell }(\text{k})$
that act as the identity on both
$M\in \mathbf{PG}_{n}^{\ell }(\text{k})$
that act as the identity on both
The group
![]() $\mathbf{LG}_{n}^{\ell }(\text{k})$
is defined to be the
$\mathbf{LG}_{n}^{\ell }(\text{k})$
is defined to be the
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
-stabilizer of the isotropic flag
$\mathbf{PG}_{n}^{\ell }(\text{k})$
-stabilizer of the isotropic flag
The group
![]() $\mathbf{LG}_{n}^{\ell }(\text{k})$
is thus isomorphic to
$\mathbf{LG}_{n}^{\ell }(\text{k})$
is thus isomorphic to
![]() $\operatorname{GL}_{\ell }(\text{k})\times \mathbf{G}_{n-\ell }(\text{k})$
. Finally, define
$\operatorname{GL}_{\ell }(\text{k})\times \mathbf{G}_{n-\ell }(\text{k})$
. Finally, define
We thus have
![]() $\mathbf{FG}_{n}^{\ell }(\text{k})\subset \mathbf{PG}_{n}^{\ell }(\text{k})$
.
$\mathbf{FG}_{n}^{\ell }(\text{k})\subset \mathbf{PG}_{n}^{\ell }(\text{k})$
.
Orthogonal groups
Finally, assume that
![]() $\mathbf{G}_{n}$
is either
$\mathbf{G}_{n}$
is either
![]() $\operatorname{SO}_{n,n}$
or
$\operatorname{SO}_{n,n}$
or
![]() $\operatorname{SO}_{n,n+1}$
. For an appropriate
$\operatorname{SO}_{n,n+1}$
. For an appropriate
![]() $m$
, the group
$m$
, the group
![]() $\mathbf{G}_{n}(\text{k})$
is then the subgroup of
$\mathbf{G}_{n}(\text{k})$
is then the subgroup of
![]() $\operatorname{SL}_{m}(\text{k})$
consisting of elements that preserve a quadratic form
$\operatorname{SL}_{m}(\text{k})$
consisting of elements that preserve a quadratic form
![]() $q(\cdot )$
on
$q(\cdot )$
on
![]() $\text{k}^{m}$
.
$\text{k}^{m}$
.
– If
 $\mathbf{G}_{n}=\operatorname{SO}_{n,n}$
, then let
$\mathbf{G}_{n}=\operatorname{SO}_{n,n}$
, then let
 $m=2n$
and let
$m=2n$
and let
 $(\vec{a}_{1},\ldots ,\vec{a}_{n},\vec{b}_{1},\ldots ,\vec{b}_{n})$
be the standard basis for
$(\vec{a}_{1},\ldots ,\vec{a}_{n},\vec{b}_{1},\ldots ,\vec{b}_{n})$
be the standard basis for
 $\text{k}^{m}$
. The group
$\text{k}^{m}$
. The group
 $\mathbf{G}_{n}(\text{k})$
is the
$\mathbf{G}_{n}(\text{k})$
is the
 $\operatorname{SL}_{m}(\text{k})$
-stabilizer of the quadratic form
$\operatorname{SL}_{m}(\text{k})$
-stabilizer of the quadratic form
 $q(\cdot )$
on
$q(\cdot )$
on
 $\text{k}^{m}$
defined via the formula
$\text{k}^{m}$
defined via the formula  $$\begin{eqnarray}q\biggl(\mathop{\sum }_{j=1}^{n}(c_{j}\vec{a}_{j}+d_{j}\vec{b}_{j})\biggr)=\mathop{\sum }_{j=1}^{n}c_{j}d_{j}\quad (c_{j},d_{j}\in \text{k}).\end{eqnarray}$$
$$\begin{eqnarray}q\biggl(\mathop{\sum }_{j=1}^{n}(c_{j}\vec{a}_{j}+d_{j}\vec{b}_{j})\biggr)=\mathop{\sum }_{j=1}^{n}c_{j}d_{j}\quad (c_{j},d_{j}\in \text{k}).\end{eqnarray}$$
– If
 $\mathbf{G}_{n}=\operatorname{SO}_{n,n+1}$
, then let
$\mathbf{G}_{n}=\operatorname{SO}_{n,n+1}$
, then let
 $m=2n+1$
and let
$m=2n+1$
and let
 $(\vec{a}_{1},\ldots ,\vec{a}_{n},\vec{b}_{1},\ldots ,\vec{b}_{n},\vec{e})$
be the standard basis for
$(\vec{a}_{1},\ldots ,\vec{a}_{n},\vec{b}_{1},\ldots ,\vec{b}_{n},\vec{e})$
be the standard basis for
 $\text{k}^{m}$
. The group
$\text{k}^{m}$
. The group
 $\mathbf{G}_{n}(\text{k})$
is the
$\mathbf{G}_{n}(\text{k})$
is the
 $\operatorname{SL}_{m}(\text{k})$
-stabilizer of the quadratic form
$\operatorname{SL}_{m}(\text{k})$
-stabilizer of the quadratic form
 $q(\cdot )$
on
$q(\cdot )$
on
 $\text{k}^{m}$
defined via the formula
$\text{k}^{m}$
defined via the formula  $$\begin{eqnarray}q\biggl(\unicode[STIX]{x1D706}\vec{e}+\mathop{\sum }_{j=1}^{n}(c_{j}\vec{a}_{j}+d_{j}\vec{b}_{j})\biggr)=\unicode[STIX]{x1D706}^{2}+\mathop{\sum }_{j=1}^{n}c_{j}d_{j}\quad (c_{j},d_{j},\unicode[STIX]{x1D706}\in \text{k}).\end{eqnarray}$$
$$\begin{eqnarray}q\biggl(\unicode[STIX]{x1D706}\vec{e}+\mathop{\sum }_{j=1}^{n}(c_{j}\vec{a}_{j}+d_{j}\vec{b}_{j})\biggr)=\unicode[STIX]{x1D706}^{2}+\mathop{\sum }_{j=1}^{n}c_{j}d_{j}\quad (c_{j},d_{j},\unicode[STIX]{x1D706}\in \text{k}).\end{eqnarray}$$
In both cases, the
![]() $\text{k}$
-parabolic subgroups of
$\text{k}$
-parabolic subgroups of
![]() $\mathbf{G}_{n}(\text{k})$
are the
$\mathbf{G}_{n}(\text{k})$
are the
![]() $\mathbf{G}_{n}(\text{k})$
-stabilizers of flags of isotropic subspaces of
$\mathbf{G}_{n}(\text{k})$
-stabilizers of flags of isotropic subspaces of
![]() $\text{k}^{m}$
, that is, subspaces on which
$\text{k}^{m}$
, that is, subspaces on which
![]() $q(\cdot )$
vanishes identically. For
$q(\cdot )$
vanishes identically. For
![]() $1\leqslant \ell \leqslant n$
the group
$1\leqslant \ell \leqslant n$
the group
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
is defined to be the
$\mathbf{PG}_{n}^{\ell }(\text{k})$
is defined to be the
![]() $\mathbf{G}_{n}(\text{k})$
-stabilizer of the isotropic flag
$\mathbf{G}_{n}(\text{k})$
-stabilizer of the isotropic flag
For
![]() $\mathbf{G}_{n}=\operatorname{SO}_{n,n}$
, the group
$\mathbf{G}_{n}=\operatorname{SO}_{n,n}$
, the group
![]() $\mathbf{UG}_{n}^{\ell }(\text{k})$
is the subgroup of
$\mathbf{UG}_{n}^{\ell }(\text{k})$
is the subgroup of
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
consisting of all
$\mathbf{PG}_{n}^{\ell }(\text{k})$
consisting of all
![]() $M\in \mathbf{PG}_{n}^{\ell }(\text{k})$
that act as the identity on both
$M\in \mathbf{PG}_{n}^{\ell }(\text{k})$
that act as the identity on both
while if
![]() $\mathbf{G}_{n}=\operatorname{SO}_{n,n+1}$
, then the group
$\mathbf{G}_{n}=\operatorname{SO}_{n,n+1}$
, then the group
![]() $\mathbf{UG}_{n}^{\ell }(\text{k})$
is the subgroup of
$\mathbf{UG}_{n}^{\ell }(\text{k})$
is the subgroup of
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
consisting of all
$\mathbf{PG}_{n}^{\ell }(\text{k})$
consisting of all
![]() $M\in \mathbf{PG}_{n}^{\ell }(\text{k})$
that act as the identity on both
$M\in \mathbf{PG}_{n}^{\ell }(\text{k})$
that act as the identity on both
The group
![]() $\mathbf{LG}_{n}^{\ell }(\text{k})$
is defined to be the
$\mathbf{LG}_{n}^{\ell }(\text{k})$
is defined to be the
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
-stabilizer of the isotropic flag
$\mathbf{PG}_{n}^{\ell }(\text{k})$
-stabilizer of the isotropic flag
The group
![]() $\mathbf{LG}_{n}^{\ell }(\text{k})$
is thus isomorphic to
$\mathbf{LG}_{n}^{\ell }(\text{k})$
is thus isomorphic to
![]() $\operatorname{GL}_{\ell }(\text{k})\times \mathbf{G}_{n-\ell }(\text{k})$
. Finally, define
$\operatorname{GL}_{\ell }(\text{k})\times \mathbf{G}_{n-\ell }(\text{k})$
. Finally, define
We thus have
![]() $\mathbf{FG}_{n}^{\ell }(\text{k})\subset \mathbf{PG}_{n}^{\ell }(\text{k})$
.
$\mathbf{FG}_{n}^{\ell }(\text{k})\subset \mathbf{PG}_{n}^{\ell }(\text{k})$
.
2.2 Facts about the Steinberg representation
Let
![]() $R$
be a commutative ring. The following theorem of Reeder [Reference ReederRee91] will play an important role in our proof of Theorem 1.1.
$R$
be a commutative ring. The following theorem of Reeder [Reference ReederRee91] will play an important role in our proof of Theorem 1.1.
Theorem 2.1 [Reference ReederRee91, Proposition 1.1].
Let
![]() $\mathbf{G}$
be a connected reductive group defined over a field
$\mathbf{G}$
be a connected reductive group defined over a field
![]() $\text{k}$
, let
$\text{k}$
, let
![]() $\mathbf{PG}(\text{k})$
be a
$\mathbf{PG}(\text{k})$
be a
![]() $\text{k}$
-parabolic subgroup of
$\text{k}$
-parabolic subgroup of
![]() $\mathbf{G}(\text{k})$
, and let
$\mathbf{G}(\text{k})$
, and let
![]() $\mathbf{LG}(\text{k})$
be a Levi component of
$\mathbf{LG}(\text{k})$
be a Levi component of
![]() $\mathbf{PG}(\text{k})$
. Then there exists an
$\mathbf{PG}(\text{k})$
. Then there exists an
![]() $\mathbf{LG}(\text{k})$
-equivariant map
$\mathbf{LG}(\text{k})$
-equivariant map
such that the induced map
is an isomorphism.
Remark 2.2. The map in Theorem 2.1 is not unique; for instance, it can be post-composed with any element of the unipotent radical of
![]() $\mathbf{PG}(\text{k})$
. The paper [Reference ReederRee91] contains a specific construction of this map, and whenever we refer to the map in Theorem 2.1 we mean the one constructed in [Reference ReederRee91].
$\mathbf{PG}(\text{k})$
. The paper [Reference ReederRee91] contains a specific construction of this map, and whenever we refer to the map in Theorem 2.1 we mean the one constructed in [Reference ReederRee91].
We wish to apply this to the distinguished parabolic subgroups
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
that we introduced in § 2.1. To do this, we need to identify
$\mathbf{PG}_{n}^{\ell }(\text{k})$
that we introduced in § 2.1. To do this, we need to identify
![]() $\operatorname{St}_{\mathbf{LG}_{n}^{\ell }}(\text{k};R)$
.
$\operatorname{St}_{\mathbf{LG}_{n}^{\ell }}(\text{k};R)$
.
Lemma 2.3. Let
![]() $\mathbf{G}_{n}$
be either
$\mathbf{G}_{n}$
be either
![]() $\operatorname{GL}_{n}$
,
$\operatorname{GL}_{n}$
,
![]() $\operatorname{SL}_{n}$
,
$\operatorname{SL}_{n}$
,
![]() $\operatorname{Sp}_{2n}$
,
$\operatorname{Sp}_{2n}$
,
![]() $\operatorname{SO}_{n,n}$
, or
$\operatorname{SO}_{n,n}$
, or
![]() $\operatorname{SO}_{n,n+1}$
. Then for all fields
$\operatorname{SO}_{n,n+1}$
. Then for all fields
![]() $\text{k}$
and all commutative rings
$\text{k}$
and all commutative rings
![]() $R$
, we have
$R$
, we have
for
![]() $1\leqslant \ell \leqslant n$
.
$1\leqslant \ell \leqslant n$
.
Proof. For
![]() $\mathbf{G}_{n}\neq \operatorname{SL}_{n}$
, this follows from the decomposition
$\mathbf{G}_{n}\neq \operatorname{SL}_{n}$
, this follows from the decomposition
![]() $\mathbf{LG}_{n}^{\ell }(\text{k})=\operatorname{GL}_{\ell }(\text{k})\times \mathbf{G}_{n-\ell }(\text{k})$
. For
$\mathbf{LG}_{n}^{\ell }(\text{k})=\operatorname{GL}_{\ell }(\text{k})\times \mathbf{G}_{n-\ell }(\text{k})$
. For
![]() $\mathbf{G}_{n}=\operatorname{SL}_{n}$
, we instead have that
$\mathbf{G}_{n}=\operatorname{SL}_{n}$
, we instead have that
![]() $\mathbf{LG}_{n}^{\ell }(\text{k})$
is the subgroup of
$\mathbf{LG}_{n}^{\ell }(\text{k})$
is the subgroup of
![]() $\operatorname{GL}_{\ell }(\text{k})\times \operatorname{GL}_{n-\ell }(\text{k})$
consisting of matrices of determinant
$\operatorname{GL}_{\ell }(\text{k})\times \operatorname{GL}_{n-\ell }(\text{k})$
consisting of matrices of determinant
![]() $1$
. The lemma in this case follows from two facts.
$1$
. The lemma in this case follows from two facts.
– There is a bijection between
 $\text{k}$
-parabolic subgroups of
$\text{k}$
-parabolic subgroups of
 $\operatorname{GL}_{n-\ell }(\text{k})$
and
$\operatorname{GL}_{n-\ell }(\text{k})$
and
 $\operatorname{SL}_{n-\ell }(\text{k})$
, and thus an
$\operatorname{SL}_{n-\ell }(\text{k})$
, and thus an
 $\operatorname{SL}_{n-\ell }(\text{k})$
-equivariant isomorphism between
$\operatorname{SL}_{n-\ell }(\text{k})$
-equivariant isomorphism between
 $\operatorname{St}_{\operatorname{GL}_{n-\ell }}(\text{k};R)$
and
$\operatorname{St}_{\operatorname{GL}_{n-\ell }}(\text{k};R)$
and
 $\operatorname{St}_{\operatorname{SL}_{n-\ell }}(\text{k};R)$
.
$\operatorname{St}_{\operatorname{SL}_{n-\ell }}(\text{k};R)$
.– There is a bijection between
 $\text{k}$
-parabolic subgroups of
$\text{k}$
-parabolic subgroups of
 $\operatorname{GL}_{\ell }(\text{k})\times \operatorname{GL}_{n-\ell }(\text{k})$
and
$\operatorname{GL}_{\ell }(\text{k})\times \operatorname{GL}_{n-\ell }(\text{k})$
and
 $\mathbf{LG}_{n}^{\ell }(\text{k})$
, and thus an
$\mathbf{LG}_{n}^{\ell }(\text{k})$
, and thus an
 $\mathbf{LG}_{n}^{\ell }(\text{k})$
-equivariant isomorphism between
$\mathbf{LG}_{n}^{\ell }(\text{k})$
-equivariant isomorphism between
 $\operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\operatorname{GL}_{n-\ell }}(\text{k};R)$
and
$\operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\operatorname{GL}_{n-\ell }}(\text{k};R)$
and
 $\operatorname{St}_{\mathbf{LG}_{n}^{\ell }}(\text{k};R)$
.
$\operatorname{St}_{\mathbf{LG}_{n}^{\ell }}(\text{k};R)$
.
Both of these bijections come from taking intersections. ◻
These two results allow us to make the following definition.
Definition 2.4. Let
![]() $\mathbf{G}_{n}$
be either
$\mathbf{G}_{n}$
be either
![]() $\operatorname{GL}_{n}$
,
$\operatorname{GL}_{n}$
,
![]() $\operatorname{SL}_{n}$
,
$\operatorname{SL}_{n}$
,
![]() $\operatorname{Sp}_{2n}$
,
$\operatorname{Sp}_{2n}$
,
![]() $\operatorname{SO}_{n,n}$
, or
$\operatorname{SO}_{n,n}$
, or
![]() $\operatorname{SO}_{n,n+1}$
. Also, let
$\operatorname{SO}_{n,n+1}$
. Also, let
![]() $\text{k}$
be a field and
$\text{k}$
be a field and
![]() $R$
be a commutative ring. For
$R$
be a commutative ring. For
![]() $1\leqslant \ell \leqslant n$
, the Reeder product map is the map
$1\leqslant \ell \leqslant n$
, the Reeder product map is the map
Remark 2.5. Identifying
![]() $\operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-\ell }}(\text{k};R)$
with its image in
$\operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-\ell }}(\text{k};R)$
with its image in
![]() $\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
under the Reeder product map, one way of viewing Theorem 2.1 is that it asserts that
$\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
under the Reeder product map, one way of viewing Theorem 2.1 is that it asserts that
We will also need the following lemma, which is precisely the case
![]() $i=0$
of Theorem 1.1. It generalizes [Reference Lee and SzczarbaLS76, Theorem 4.1]. Recall that if
$i=0$
of Theorem 1.1. It generalizes [Reference Lee and SzczarbaLS76, Theorem 4.1]. Recall that if
![]() $G$
is a group and
$G$
is a group and
![]() $M$
is a
$M$
is a
![]() $G$
-module, then the coinvariants
$G$
-module, then the coinvariants
![]() $M_{G}$
are the largest quotient of
$M_{G}$
are the largest quotient of
![]() $M$
on which
$M$
on which
![]() $G$
acts trivially. The coinvariants
$G$
acts trivially. The coinvariants
![]() $M_{G}$
are isomorphic to
$M_{G}$
are isomorphic to
![]() $\operatorname{H}_{0}(G;M)$
.
$\operatorname{H}_{0}(G;M)$
.
Lemma 2.6. Let
![]() $\mathbf{G}_{n}$
be either
$\mathbf{G}_{n}$
be either
![]() $\operatorname{GL}_{n}$
,
$\operatorname{GL}_{n}$
,
![]() $\operatorname{SL}_{n}$
,
$\operatorname{SL}_{n}$
,
![]() $\operatorname{Sp}_{2n}$
,
$\operatorname{Sp}_{2n}$
,
![]() $\operatorname{SO}_{n,n}$
, or
$\operatorname{SO}_{n,n}$
, or
![]() $\operatorname{SO}_{n,n+1}$
. Then for all fields
$\operatorname{SO}_{n,n+1}$
. Then for all fields
![]() $\text{k}$
and all commutative rings
$\text{k}$
and all commutative rings
![]() $R$
, we have
$R$
, we have
![]() $(\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))_{\mathbf{G}_{n}(\text{k};R)}=0$
for
$(\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))_{\mathbf{G}_{n}(\text{k};R)}=0$
for
![]() $n\geqslant 2$
.
$n\geqslant 2$
.
Proof. Theorem 2.1 implies that
It is thus enough to prove that
Whatever
![]() $\mathbf{G}_{n}$
is, the group
$\mathbf{G}_{n}$
is, the group
![]() $\mathbf{LG}_{n}^{2}(\text{k})$
contains the subgroup
$\mathbf{LG}_{n}^{2}(\text{k})$
contains the subgroup
![]() $\operatorname{SL}_{2}(\text{k})\times 1$
. It is thus enough to prove that
$\operatorname{SL}_{2}(\text{k})\times 1$
. It is thus enough to prove that
This is an easy exercise using the fact that
where
![]() $\mathbb{P}^{1}(\text{k})$
is the projective line over
$\mathbb{P}^{1}(\text{k})$
is the projective line over
![]() $\text{k}$
, regarded as a discrete set of points. For details, see [Reference Lee and SzczarbaLS76, Theorem 4.1].◻
$\text{k}$
, regarded as a discrete set of points. For details, see [Reference Lee and SzczarbaLS76, Theorem 4.1].◻
3 Reduction to stability
Let
![]() $\mathbf{G}_{n}$
be either
$\mathbf{G}_{n}$
be either
![]() $\operatorname{GL}_{n}$
,
$\operatorname{GL}_{n}$
,
![]() $\operatorname{SL}_{n}$
,
$\operatorname{SL}_{n}$
,
![]() $\operatorname{Sp}_{2n}$
,
$\operatorname{Sp}_{2n}$
,
![]() $\operatorname{SO}_{n,n}$
, or
$\operatorname{SO}_{n,n}$
, or
![]() $\operatorname{SO}_{n,n+1}$
. Let
$\operatorname{SO}_{n,n+1}$
. Let
![]() $\text{k}$
be a field and
$\text{k}$
be a field and
![]() $R$
be a commutative ring. In this section, we reduce Theorem 1.1 to an appropriate homological stability theorem.
$R$
be a commutative ring. In this section, we reduce Theorem 1.1 to an appropriate homological stability theorem.
Fix some
![]() $i\geqslant 0$
and some
$i\geqslant 0$
and some
![]() $n\geqslant 2$
. The stabilization map for
$n\geqslant 2$
. The stabilization map for
![]() $\operatorname{H}_{i}(\mathbf{G}_{n-1}(\text{k});\operatorname{St}_{\mathbf{G}_{n-1}}(\text{k};R))$
is the map
$\operatorname{H}_{i}(\mathbf{G}_{n-1}(\text{k});\operatorname{St}_{\mathbf{G}_{n-1}}(\text{k};R))$
is the map
induced by the following two maps.
– The group homomorphism
 $\mathbf{G}_{n-1}(\text{k})\rightarrow \mathbf{G}_{n}(\text{k})$
obtained as follows. The group
$\mathbf{G}_{n-1}(\text{k})\rightarrow \mathbf{G}_{n}(\text{k})$
obtained as follows. The group
 $\mathbf{LG}_{n}^{1}(\text{k})$
is a subgroup of
$\mathbf{LG}_{n}^{1}(\text{k})$
is a subgroup of
 $\operatorname{GL}_{1}(\text{k})\times \mathbf{G}_{n-1}(\text{k})$
that contains the subgroup
$\operatorname{GL}_{1}(\text{k})\times \mathbf{G}_{n-1}(\text{k})$
that contains the subgroup
 $1\times \mathbf{G}_{n-1}(\text{k})$
. In fact,
$1\times \mathbf{G}_{n-1}(\text{k})$
. In fact,
 $\mathbf{LG}_{n}^{1}(\text{k})=\operatorname{GL}_{1}(\text{k})\times \mathbf{G}_{n-1}(\text{k})$
except when
$\mathbf{LG}_{n}^{1}(\text{k})=\operatorname{GL}_{1}(\text{k})\times \mathbf{G}_{n-1}(\text{k})$
except when
 $\mathbf{G}_{n}=\operatorname{SL}_{n}$
. We can thus define a homomorphism
$\mathbf{G}_{n}=\operatorname{SL}_{n}$
. We can thus define a homomorphism
 $\mathbf{G}_{n-1}(\text{k})\rightarrow \mathbf{G}_{n}(\text{k})$
via the composition
$\mathbf{G}_{n-1}(\text{k})\rightarrow \mathbf{G}_{n}(\text{k})$
via the composition  $$\begin{eqnarray}\mathbf{G}_{n-1}(\text{k})=1\times \mathbf{G}_{n-1}(\text{k}){\hookrightarrow}\mathbf{LG}_{n}^{1}(\text{k}){\hookrightarrow}\mathbf{G}_{n}(\text{k}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{G}_{n-1}(\text{k})=1\times \mathbf{G}_{n-1}(\text{k}){\hookrightarrow}\mathbf{LG}_{n}^{1}(\text{k}){\hookrightarrow}\mathbf{G}_{n}(\text{k}).\end{eqnarray}$$
– The map
 $\operatorname{St}_{\mathbf{G}_{n-1}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
that equals the composition where the final arrow is the Reeder product map. Here we are using the convention regarding the empty set discussed at the end of the introduction which implies that
$\operatorname{St}_{\mathbf{G}_{n-1}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
that equals the composition where the final arrow is the Reeder product map. Here we are using the convention regarding the empty set discussed at the end of the introduction which implies that $$\begin{eqnarray}\operatorname{St}_{\mathbf{G}_{n-1}}(\text{k};R)\cong R\otimes \operatorname{St}_{\mathbf{G}_{n-1}}(\text{k};R)\cong \operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-1}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{St}_{\mathbf{G}_{n-1}}(\text{k};R)\cong R\otimes \operatorname{St}_{\mathbf{G}_{n-1}}(\text{k};R)\cong \operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-1}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R),\end{eqnarray}$$
 $\operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)=R$
; this convention is compatible with Theorem 2.1.
$\operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)=R$
; this convention is compatible with Theorem 2.1.
The main result of this section is then as follows.
Lemma 3.1. Let
![]() $\mathbf{G}_{n}$
be either
$\mathbf{G}_{n}$
be either
![]() $\operatorname{GL}_{n}$
,
$\operatorname{GL}_{n}$
,
![]() $\operatorname{SL}_{n}$
,
$\operatorname{SL}_{n}$
,
![]() $\operatorname{Sp}_{2n}$
,
$\operatorname{Sp}_{2n}$
,
![]() $\operatorname{SO}_{n,n}$
, or
$\operatorname{SO}_{n,n}$
, or
![]() $\operatorname{SO}_{n,n+1}$
. Let
$\operatorname{SO}_{n,n+1}$
. Let
![]() $\text{k}$
be a field and let
$\text{k}$
be a field and let
![]() $R$
be a commutative ring. Assume that the stabilization map (3.1) is a surjection for
$R$
be a commutative ring. Assume that the stabilization map (3.1) is a surjection for
![]() $n\geqslant N$
. Then
$n\geqslant N$
. Then
![]() $\operatorname{H}_{i}(\mathbf{G}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))=0$
for
$\operatorname{H}_{i}(\mathbf{G}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))=0$
for
![]() $n\geqslant N+1$
.
$n\geqslant N+1$
.
Proof. Consider
![]() $n\geqslant N+1$
. By assumption, the map
$n\geqslant N+1$
. By assumption, the map
obtained by iterating the stabilization map twice is surjective. It is thus enough to show that the image of this map is
![]() $0$
. We can factor this map as
$0$
. We can factor this map as
Regard
![]() $\operatorname{SL}_{2}(\text{k})$
as a subgroup of
$\operatorname{SL}_{2}(\text{k})$
as a subgroup of
![]() $\mathbf{G}_{n}(\text{k})$
via the composition
$\mathbf{G}_{n}(\text{k})$
via the composition
The subgroup
![]() $\operatorname{SL}_{2}(\text{k})$
of
$\operatorname{SL}_{2}(\text{k})$
of
![]() $\mathbf{G}_{n}(\text{k})$
commutes with the image of
$\mathbf{G}_{n}(\text{k})$
commutes with the image of
![]() $\mathbf{G}_{n-2}(\text{k})$
in
$\mathbf{G}_{n-2}(\text{k})$
in
![]() $\mathbf{G}_{n}(\text{k})$
under the map used to define (3.2). Inner automorphisms act trivially on homology, even with twisted coefficients; see [Reference BrownBro94, Proposition III.8.1]. It follows that to show that the image of (3.2) is
$\mathbf{G}_{n}(\text{k})$
under the map used to define (3.2). Inner automorphisms act trivially on homology, even with twisted coefficients; see [Reference BrownBro94, Proposition III.8.1]. It follows that to show that the image of (3.2) is
![]() $0$
, it is enough to prove that
$0$
, it is enough to prove that
This is equivalent to
which is one case of Lemma 2.6.◻
4 The stabilizer subgroups
This section constructs an isomorphism (Lemma 4.1 below) that will play a fundamental role in our proof of Theorem 1.1.
Let
![]() $\mathbf{G}_{n}$
be either
$\mathbf{G}_{n}$
be either
![]() $\operatorname{GL}_{n}$
,
$\operatorname{GL}_{n}$
,
![]() $\operatorname{SL}_{n}$
,
$\operatorname{SL}_{n}$
,
![]() $\operatorname{Sp}_{2n}$
,
$\operatorname{Sp}_{2n}$
,
![]() $\operatorname{SO}_{n,n}$
, or
$\operatorname{SO}_{n,n}$
, or
![]() $\operatorname{SO}_{n,n+1}$
. Let
$\operatorname{SO}_{n,n+1}$
. Let
![]() $\text{k}$
be a field and
$\text{k}$
be a field and
![]() $R$
be a commutative ring. Fix some
$R$
be a commutative ring. Fix some
![]() $1\leqslant \ell \leqslant n$
. There is a map
$1\leqslant \ell \leqslant n$
. There is a map
induced by the following two maps:
– the inclusion map
 $1\times \mathbf{G}_{n-\ell }(\text{k})\rightarrow \mathbf{FG}_{n}^{\ell }(\text{k})$
(here we are regarding
$1\times \mathbf{G}_{n-\ell }(\text{k})\rightarrow \mathbf{FG}_{n}^{\ell }(\text{k})$
(here we are regarding
 $\mathbf{FG}_{n}^{\ell }(\text{k})$
as a subgroup of
$\mathbf{FG}_{n}^{\ell }(\text{k})$
as a subgroup of
 $\mathbf{PG}_{n}^{\ell }(\text{k})$
that contains
$\mathbf{PG}_{n}^{\ell }(\text{k})$
that contains
 $1\times \mathbf{G}_{n-\ell }(\text{k})\subset \mathbf{LG}_{n}^{\ell }(\text{k})\subset \mathbf{PG}_{n}^{\ell }(\text{k})$
);
$1\times \mathbf{G}_{n-\ell }(\text{k})\subset \mathbf{LG}_{n}^{\ell }(\text{k})\subset \mathbf{PG}_{n}^{\ell }(\text{k})$
);– the Reeder product map
 $\operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-\ell }}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
.
$\operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-\ell }}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
.
Our main result is as follows.
Lemma 4.1. Let
![]() $\text{k}$
be a field, let
$\text{k}$
be a field, let
![]() $R$
be a commutative ring, let
$R$
be a commutative ring, let
![]() $1\leqslant \ell \leqslant n$
, and let
$1\leqslant \ell \leqslant n$
, and let
![]() $i\geqslant 0$
. Then the map (4.1) is an isomorphism.
$i\geqslant 0$
. Then the map (4.1) is an isomorphism.
Proof. Shapiro’s Lemma [Reference BrownBro94, Proposition III.6.2] gives an isomorphism
Below we will prove that there is an isomorphism
of
![]() $\mathbf{FG}_{n}^{\ell }(\text{k})$
-representations. Combined with the above, this will yield an isomorphism between the left- and right-hand sides of (4.1), which is easily seen to be the map in (4.1).
$\mathbf{FG}_{n}^{\ell }(\text{k})$
-representations. Combined with the above, this will yield an isomorphism between the left- and right-hand sides of (4.1), which is easily seen to be the map in (4.1).
It remains to construct the isomorphism (4.2). Since
![]() $\mathbf{FG}_{n}^{\ell }(\text{k})\subset \mathbf{PG}_{n}^{\ell }(\text{k})$
, we can restrict the isomorphism given by Theorem 2.1 and Lemma 2.3 to obtain an isomorphism
$\mathbf{FG}_{n}^{\ell }(\text{k})\subset \mathbf{PG}_{n}^{\ell }(\text{k})$
, we can restrict the isomorphism given by Theorem 2.1 and Lemma 2.3 to obtain an isomorphism
The unipotent radical of
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
is contained in
$\mathbf{PG}_{n}^{\ell }(\text{k})$
is contained in
![]() $\mathbf{FG}_{n}^{\ell }(\text{k})$
. This implies that there is a single
$\mathbf{FG}_{n}^{\ell }(\text{k})$
. This implies that there is a single
![]() $(\mathbf{FG}_{n}^{\ell }(\text{k}),\mathbf{LG}_{n}^{\ell }(\text{k}))$
-double coset in
$(\mathbf{FG}_{n}^{\ell }(\text{k}),\mathbf{LG}_{n}^{\ell }(\text{k}))$
-double coset in
![]() $\mathbf{PG}_{n}^{\ell }(\text{k})$
. Also,
$\mathbf{PG}_{n}^{\ell }(\text{k})$
. Also,
![]() $\mathbf{FG}_{n}^{\ell }(\text{k})\cap \mathbf{LG}_{n}^{\ell }(\text{k})=\mathbf{G}_{n-\ell }(\text{k})$
. The double coset formula [Reference BrownBro94, Proposition III.5.6b] therefore implies that the left side of (4.3) is canonically isomorphic to
$\mathbf{FG}_{n}^{\ell }(\text{k})\cap \mathbf{LG}_{n}^{\ell }(\text{k})=\mathbf{G}_{n-\ell }(\text{k})$
. The double coset formula [Reference BrownBro94, Proposition III.5.6b] therefore implies that the left side of (4.3) is canonically isomorphic to
as desired.◻
The following alternate version of Lemma 4.1 will be useful.
Corollary 4.2. Let
![]() $\text{k}$
be a field, let
$\text{k}$
be a field, let
![]() $R$
be a commutative ring, let
$R$
be a commutative ring, let
![]() $1\leqslant \ell \leqslant n$
, and let
$1\leqslant \ell \leqslant n$
, and let
![]() $i\geqslant 0$
. Then there exists an isomorphism
$i\geqslant 0$
. Then there exists an isomorphism
Proof. Since
![]() $\operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)$
is a free
$\operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)$
is a free
![]() $R$
-module, we have
$R$
-module, we have
The corollary now follows from Lemma 4.1.◻
We will also need an explicit inverse
to the isomorphism (4.1). The map (4.4) will be induced by the following two maps:
– the homomorphism
 $\mathbf{FG}_{n}^{\ell }(\text{k})\rightarrow 1\times \mathbf{G}_{n-\ell }(\text{k})$
obtained by restricting the projection
$\mathbf{FG}_{n}^{\ell }(\text{k})\rightarrow 1\times \mathbf{G}_{n-\ell }(\text{k})$
obtained by restricting the projection
 $\mathbf{PG}_{n}^{\ell }(\text{k})\rightarrow \mathbf{LG}_{n}^{\ell }(\text{k})$
to
$\mathbf{PG}_{n}^{\ell }(\text{k})\rightarrow \mathbf{LG}_{n}^{\ell }(\text{k})$
to
 $\mathbf{FG}_{n}^{\ell }(\text{k})$
;
$\mathbf{FG}_{n}^{\ell }(\text{k})$
;– the map
which equals the composition $$\begin{eqnarray}\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)\rightarrow \operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-\ell }}(\text{k};R)\end{eqnarray}$$
where the first equality comes from a combination of Theorem 2.1 and Lemma 2.3 (see Remark 2.5) and the last arrow takes
$$\begin{eqnarray}\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)\rightarrow \operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-\ell }}(\text{k};R)\end{eqnarray}$$
where the first equality comes from a combination of Theorem 2.1 and Lemma 2.3 (see Remark 2.5) and the last arrow takes $$\begin{eqnarray}\displaystyle \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R) & = & \displaystyle \mathop{\bigoplus }_{u\in \mathbf{UG}_{n}^{\ell }(\text{k})}u\cdot (\operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-\ell }}(\text{k};R))\nonumber\\ \displaystyle & \rightarrow & \displaystyle \operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-\ell }}(\text{k};R),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R) & = & \displaystyle \mathop{\bigoplus }_{u\in \mathbf{UG}_{n}^{\ell }(\text{k})}u\cdot (\operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-\ell }}(\text{k};R))\nonumber\\ \displaystyle & \rightarrow & \displaystyle \operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-\ell }}(\text{k};R),\nonumber\end{eqnarray}$$
 $u\cdot x\in u\cdot (\operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-\ell }}(\text{k};R))$
to
$u\cdot x\in u\cdot (\operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-\ell }}(\text{k};R))$
to
 $x\in \operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-\ell }}(\text{k};R)$
(we will call this map the Reeder projection map).
$x\in \operatorname{St}_{\operatorname{GL}_{\ell }}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-\ell }}(\text{k};R)$
(we will call this map the Reeder projection map).
It is clear that these define a map of the form (4.4). The following lemma says that this is an inverse to (4.1).
Lemma 4.3. Let
![]() $\text{k}$
be a field, let
$\text{k}$
be a field, let
![]() $R$
be a commutative ring, let
$R$
be a commutative ring, let
![]() $1\leqslant \ell \leqslant n$
, and let
$1\leqslant \ell \leqslant n$
, and let
![]() $i\geqslant 0$
. Then the map (4.4) is an inverse to the map (4.1).
$i\geqslant 0$
. Then the map (4.4) is an inverse to the map (4.1).
Proof. The proof follows immediately from the fact that the compositions
and
of the maps used to define (4.1) and (4.4) equal the identity.◻
5 Vanishing
This section is devoted to the proof of Theorem 1.1. The actual proof is in § 5.3. This is preceded by two sections of preliminaries.
5.1 Equivariant homology
In our proof of Theorem 1.1, we will need some basic facts about equivariant homology. A basic reference is [Reference BrownBro94, ch. VII.7].
Let
![]() $G$
be a group, let
$G$
be a group, let
![]() $X$
be a semisimplicial set on which
$X$
be a semisimplicial set on which
![]() $G$
acts, let
$G$
acts, let
![]() $R$
be a ring, and let
$R$
be a ring, and let
![]() $M$
be an
$M$
be an
![]() $R[G]$
-module. Let
$R[G]$
-module. Let
![]() $EG$
be a contractible semisimplicial set on which
$EG$
be a contractible semisimplicial set on which
![]() $G$
acts freely and let
$G$
acts freely and let
![]() $BG=EG/G$
, so
$BG=EG/G$
, so
![]() $BG$
is a classifying space for
$BG$
is a classifying space for
![]() $G$
. Denote by
$G$
. Denote by
![]() $EG\times _{G}X$
the quotient of
$EG\times _{G}X$
the quotient of
![]() $EG\times X$
by the diagonal action of
$EG\times X$
by the diagonal action of
![]() $G$
. This is known as the Borel construction. The homotopy type of
$G$
. This is known as the Borel construction. The homotopy type of
![]() $EG\times _{G}X$
does not depend on the choice of
$EG\times _{G}X$
does not depend on the choice of
![]() $EG$
. The projection
$EG$
. The projection
![]() $EG\times _{G}X\rightarrow EG/G=BG$
induces a homomorphism
$EG\times _{G}X\rightarrow EG/G=BG$
induces a homomorphism
![]() $\unicode[STIX]{x1D70B}_{1}(EG\times _{G}X)\rightarrow \unicode[STIX]{x1D70B}_{1}(BG)=G$
. Via this homomorphism, we can regard
$\unicode[STIX]{x1D70B}_{1}(EG\times _{G}X)\rightarrow \unicode[STIX]{x1D70B}_{1}(BG)=G$
. Via this homomorphism, we can regard
![]() $M$
as a local coefficient system on
$M$
as a local coefficient system on
![]() $EG\times _{G}X$
. The
$EG\times _{G}X$
. The
![]() $G$
-equivariant homology groups of
$G$
-equivariant homology groups of
![]() $X$
with coefficients in
$X$
with coefficients in
![]() $M$
, denoted
$M$
, denoted
![]() $\operatorname{H}_{\ast }^{G}(X;M)$
, are the homology groups of
$\operatorname{H}_{\ast }^{G}(X;M)$
, are the homology groups of
![]() $EG\times _{G}X$
with respect to the local coefficient system
$EG\times _{G}X$
with respect to the local coefficient system
![]() $M$
.
$M$
.
Lemma 5.1. If
![]() $X$
is
$X$
is
![]() $\ell$
-connected, then the above map
$\ell$
-connected, then the above map
![]() $EG\times _{G}X\rightarrow EG/G=BG$
induces an isomorphism
$EG\times _{G}X\rightarrow EG/G=BG$
induces an isomorphism
![]() $\operatorname{H}_{i}^{G}(X;M)\cong \operatorname{H}_{i}(G;M)$
for
$\operatorname{H}_{i}^{G}(X;M)\cong \operatorname{H}_{i}(G;M)$
for
![]() $0\leqslant i\leqslant \ell$
and a surjection
$0\leqslant i\leqslant \ell$
and a surjection
![]() $\operatorname{H}_{\ell +1}^{G}(X;M)\rightarrow \operatorname{H}_{\ell +1}(X;M)$
.
$\operatorname{H}_{\ell +1}^{G}(X;M)\rightarrow \operatorname{H}_{\ell +1}(X;M)$
.
Proof. The group
![]() $G$
acts freely on
$G$
acts freely on
![]() $EG\times X$
and
$EG\times X$
and
![]() $EG\times X$
is
$EG\times X$
is
![]() $\ell$
-connected. Viewing
$\ell$
-connected. Viewing
![]() $EG\times X$
as a CW-complex, we can make
$EG\times X$
as a CW-complex, we can make
![]() $EG\times X$
contractible by adding cells of dimension at least
$EG\times X$
contractible by adding cells of dimension at least
![]() $(\ell +2)$
. We conclude that there exists a classifying space for
$(\ell +2)$
. We conclude that there exists a classifying space for
![]() $G$
whose
$G$
whose
![]() $(\ell +1)$
-skeleton equals the
$(\ell +1)$
-skeleton equals the
![]() $(\ell +1)$
-skeleton of
$(\ell +1)$
-skeleton of
![]() $EG\times _{G}X$
. The lemma follows.◻
$EG\times _{G}X$
. The lemma follows.◻
Our main tool for understanding
![]() $\operatorname{H}_{\ast }^{G}(X;M)$
is the following spectral sequence, which is constructed in [Reference BrownBro94, Equation VII.7.7].
$\operatorname{H}_{\ast }^{G}(X;M)$
is the following spectral sequence, which is constructed in [Reference BrownBro94, Equation VII.7.7].
Lemma 5.2. For all
![]() $p\geqslant 0$
, let
$p\geqslant 0$
, let
![]() $\unicode[STIX]{x1D6F4}_{p}$
be a set containing exactly one representative for each orbit of the action of
$\unicode[STIX]{x1D6F4}_{p}$
be a set containing exactly one representative for each orbit of the action of
![]() $G$
on the
$G$
on the
![]() $p$
-simplices of
$p$
-simplices of
![]() $X$
. For
$X$
. For
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}_{p}$
, let
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}_{p}$
, let
![]() $G_{\unicode[STIX]{x1D70E}}$
be the stabilizer of
$G_{\unicode[STIX]{x1D70E}}$
be the stabilizer of
![]() $\unicode[STIX]{x1D70E}$
. Then there is a first quadrant spectral sequence
$\unicode[STIX]{x1D70E}$
. Then there is a first quadrant spectral sequence
Remark 5.3. In [Reference BrownBro94, Equation VII.7.7], the action of
![]() $G_{\unicode[STIX]{x1D70E}}$
on
$G_{\unicode[STIX]{x1D70E}}$
on
![]() $M$
is twisted by an ‘orientation character’; however, this is unnecessary in our situation, since we are working with semisimplicial sets rather than ordinary simplicial complexes (the point being that in the geometric realization, the setwise stabilizer of a simplex stabilizes the simplex pointwise).
$M$
is twisted by an ‘orientation character’; however, this is unnecessary in our situation, since we are working with semisimplicial sets rather than ordinary simplicial complexes (the point being that in the geometric realization, the setwise stabilizer of a simplex stabilizes the simplex pointwise).
5.2 Complexes of partial bases
Let
![]() $\text{k}$
be a field and let
$\text{k}$
be a field and let
![]() $\mathbf{G}_{n}$
be either
$\mathbf{G}_{n}$
be either
![]() $\operatorname{GL}_{n}$
,
$\operatorname{GL}_{n}$
,
![]() $\operatorname{SL}_{n}$
,
$\operatorname{SL}_{n}$
,
![]() $\operatorname{Sp}_{2n}$
,
$\operatorname{Sp}_{2n}$
,
![]() $\operatorname{SO}_{n,n}$
, or
$\operatorname{SO}_{n,n}$
, or
![]() $\operatorname{SO}_{n,n+1}$
. To prove Theorem 1.1, we will need to construct a highly connected space
$\operatorname{SO}_{n,n+1}$
. To prove Theorem 1.1, we will need to construct a highly connected space
![]() $\mathbf{CG}_{n}(\text{k})$
on which
$\mathbf{CG}_{n}(\text{k})$
on which
![]() $\mathbf{G}_{n}(\text{k})$
acts. The definition of this complex is as follows.
$\mathbf{G}_{n}(\text{k})$
acts. The definition of this complex is as follows.
– If
 $\mathbf{G}_{n}=\operatorname{GL}_{n}$
or
$\mathbf{G}_{n}=\operatorname{GL}_{n}$
or
 $\mathbf{G}_{n}=\operatorname{SL}_{n}$
, then define
$\mathbf{G}_{n}=\operatorname{SL}_{n}$
, then define
 $\mathbf{CG}_{n}(\text{k})$
to be the complex of partial bases for
$\mathbf{CG}_{n}(\text{k})$
to be the complex of partial bases for
 $\text{k}^{n}$
, i.e. the semisimplicial complex whose
$\text{k}^{n}$
, i.e. the semisimplicial complex whose
 $\ell$
-simplices are ordered sequences
$\ell$
-simplices are ordered sequences
 $[\vec{v}_{0},\ldots ,\vec{v}_{\ell }]$
of linearly independent elements of
$[\vec{v}_{0},\ldots ,\vec{v}_{\ell }]$
of linearly independent elements of
 $\text{k}^{n}$
.
$\text{k}^{n}$
.– If
 $\mathbf{G}_{n}=\operatorname{Sp}_{2n}$
or
$\mathbf{G}_{n}=\operatorname{Sp}_{2n}$
or
 $\mathbf{G}_{n}=\operatorname{SO}_{n,n}$
or
$\mathbf{G}_{n}=\operatorname{SO}_{n,n}$
or
 $\mathbf{G}_{n}=\operatorname{SO}_{n,n+1}$
and
$\mathbf{G}_{n}=\operatorname{SO}_{n,n+1}$
and
 $\text{k}^{m}$
is the vector space upon which
$\text{k}^{m}$
is the vector space upon which
 $\mathbf{G}_{n}(\text{k})$
acts (so
$\mathbf{G}_{n}(\text{k})$
acts (so
 $m$
is either
$m$
is either
 $2n$
or
$2n$
or
 $2n+1$
), then define
$2n+1$
), then define
 $\mathbf{CG}_{n}(\text{k})$
to be the complex of partial isotropic bases for
$\mathbf{CG}_{n}(\text{k})$
to be the complex of partial isotropic bases for
 $\text{k}^{m}$
, i.e. the semisimplicial complex whose
$\text{k}^{m}$
, i.e. the semisimplicial complex whose
 $\ell$
-simplices are ordered sequences
$\ell$
-simplices are ordered sequences
 $[\vec{v}_{0},\ldots ,\vec{v}_{\ell }]$
of linearly independent elements of
$[\vec{v}_{0},\ldots ,\vec{v}_{\ell }]$
of linearly independent elements of
 $\text{k}^{m}$
that span an isotropic subspace.
$\text{k}^{m}$
that span an isotropic subspace.
The following theorem summarizes the properties of
![]() $\mathbf{CG}_{n}(\text{k})$
.
$\mathbf{CG}_{n}(\text{k})$
.
Theorem 5.4. Let
![]() $\text{k}$
be a field and let
$\text{k}$
be a field and let
![]() $\mathbf{G}_{n}$
be either
$\mathbf{G}_{n}$
be either
![]() $\operatorname{GL}_{n}$
,
$\operatorname{GL}_{n}$
,
![]() $\operatorname{SL}_{n}$
,
$\operatorname{SL}_{n}$
,
![]() $\operatorname{Sp}_{2n}$
,
$\operatorname{Sp}_{2n}$
,
![]() $\operatorname{SO}_{n,n}$
, or
$\operatorname{SO}_{n,n}$
, or
![]() $\operatorname{SO}_{n,n+1}$
. The following then hold.
$\operatorname{SO}_{n,n+1}$
. The following then hold.
(1) The group
 $\mathbf{G}_{n}(\text{k})$
acts transitively on the
$\mathbf{G}_{n}(\text{k})$
acts transitively on the
 $\ell$
-cells of
$\ell$
-cells of
 $\mathbf{CG}_{n}(\text{k})$
for all
$\mathbf{CG}_{n}(\text{k})$
for all
 $0\leqslant \ell <n-1$
.
$0\leqslant \ell <n-1$
.(2) The space
 $\mathbf{CG}_{n}(\text{k})$
is
$\mathbf{CG}_{n}(\text{k})$
is
 $f(n)$
-connected where
$f(n)$
-connected where
 $f(n)$
is given by:
$f(n)$
is given by:(a)
 $f(n)=n-2$
if
$f(n)=n-2$
if
 $\mathbf{G}_{n}$
is either
$\mathbf{G}_{n}$
is either
 $\operatorname{GL}_{n}$
or
$\operatorname{GL}_{n}$
or
 $\operatorname{SL}_{n}$
;
$\operatorname{SL}_{n}$
;(b)
 $f(n)=(n-3)/2$
if
$f(n)=(n-3)/2$
if
 $\mathbf{G}_{n}$
is either
$\mathbf{G}_{n}$
is either
 $\operatorname{Sp}_{2n}$
,
$\operatorname{Sp}_{2n}$
,
 $\operatorname{SO}_{n,n}$
, or
$\operatorname{SO}_{n,n}$
, or
 $\operatorname{SO}_{n,n+1}$
.
$\operatorname{SO}_{n,n+1}$
.
Proof. The first assertion is well known (and also holds for
![]() $\ell =n-1$
except when
$\ell =n-1$
except when
![]() $\mathbf{G}_{n}=\operatorname{SL}_{n}$
). As for the second, Maazen proved in his thesis [Reference MaazenMaa79] that
$\mathbf{G}_{n}=\operatorname{SL}_{n}$
). As for the second, Maazen proved in his thesis [Reference MaazenMaa79] that
![]() $\mathbf{CG}_{n}(\text{k})$
is
$\mathbf{CG}_{n}(\text{k})$
is
![]() $(n-2)$
-connected for
$(n-2)$
-connected for
![]() $\mathbf{G}_{n}=\operatorname{GL}_{n}$
and
$\mathbf{G}_{n}=\operatorname{GL}_{n}$
and
![]() $\mathbf{G}_{n}=\operatorname{SL}_{n}$
. See [Reference van der KallenvdK80] for a published proof of a more general result. Friedrich proved in [Reference FriedrichFri16, Theorem 3.23] that
$\mathbf{G}_{n}=\operatorname{SL}_{n}$
. See [Reference van der KallenvdK80] for a published proof of a more general result. Friedrich proved in [Reference FriedrichFri16, Theorem 3.23] that
![]() $\mathbf{CG}_{n}(\text{k})$
is
$\mathbf{CG}_{n}(\text{k})$
is
![]() $(n-3)/2$
-connected for
$(n-3)/2$
-connected for
![]() $\mathbf{G}_{n}=\operatorname{Sp}_{2n}$
and
$\mathbf{G}_{n}=\operatorname{Sp}_{2n}$
and
![]() $\mathbf{G}_{n}=\operatorname{SO}_{n,n}$
and
$\mathbf{G}_{n}=\operatorname{SO}_{n,n}$
and
![]() $\mathbf{G}_{n}=\operatorname{SO}_{n,n+1}$
(for
$\mathbf{G}_{n}=\operatorname{SO}_{n,n+1}$
(for
![]() $\operatorname{Sp}_{2n}$
and
$\operatorname{Sp}_{2n}$
and
![]() $\operatorname{SO}_{n,n}$
, this was proven earlier in [Reference Mirzaii and van der KallenMv02, Theorem 7.3]). To apply the cited result of Friedrich to our situation, we need the fact that the unitary stable rank of a field is
$\operatorname{SO}_{n,n}$
, this was proven earlier in [Reference Mirzaii and van der KallenMv02, Theorem 7.3]). To apply the cited result of Friedrich to our situation, we need the fact that the unitary stable rank of a field is
![]() $1$
(see, e.g., [Reference Mirzaii and van der KallenMv02, Example 6.5]).◻
$1$
(see, e.g., [Reference Mirzaii and van der KallenMv02, Example 6.5]).◻
5.3 The proof of Theorem 1.1
Let us first recall the statement of the theorem. Let
![]() $\mathbf{G}_{n}$
be either
$\mathbf{G}_{n}$
be either
![]() $\operatorname{GL}_{n}$
,
$\operatorname{GL}_{n}$
,
![]() $\operatorname{SL}_{n}$
,
$\operatorname{SL}_{n}$
,
![]() $\operatorname{Sp}_{2n}$
,
$\operatorname{Sp}_{2n}$
,
![]() $\operatorname{SO}_{n,n}$
, or
$\operatorname{SO}_{n,n}$
, or
![]() $\operatorname{SO}_{n,n+1}$
. Also, let
$\operatorname{SO}_{n,n+1}$
. Also, let
![]() $\text{k}$
be a field and
$\text{k}$
be a field and
![]() $R$
be a commutative ring. Our goal is to prove that
$R$
be a commutative ring. Our goal is to prove that
![]() $\operatorname{H}_{i}(\mathbf{G}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))=0$
for
$\operatorname{H}_{i}(\mathbf{G}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))=0$
for
![]() $n\geqslant 2i+2$
and that there exists a surjection
$n\geqslant 2i+2$
and that there exists a surjection
Of course, this surjection will be induced by the stabilization map defined in § 3.
The proof is by induction on
![]() $i$
. We begin with the base case
$i$
. We begin with the base case
![]() $i=0$
. Lemma 2.6 says that
$i=0$
. Lemma 2.6 says that
![]() $\operatorname{H}_{0}(\mathbf{G}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))=0$
for
$\operatorname{H}_{0}(\mathbf{G}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))=0$
for
![]() $n\geqslant 2$
, so we only need to show that the map (5.1) is a surjection for
$n\geqslant 2$
, so we only need to show that the map (5.1) is a surjection for
![]() $i=0$
. For the domain,
$i=0$
. For the domain,
![]() $\mathbf{G}_{0}(\text{k})$
is the trivial group. By our convention regarding the empty set discussed at the end of the introduction, we thus have
$\mathbf{G}_{0}(\text{k})$
is the trivial group. By our convention regarding the empty set discussed at the end of the introduction, we thus have
![]() $\operatorname{St}_{\mathbf{G}_{0}}(\text{k};R)=R$
, and hence
$\operatorname{St}_{\mathbf{G}_{0}}(\text{k};R)=R$
, and hence
![]() $\operatorname{H}_{i}(\mathbf{G}_{0}(\text{k});\operatorname{St}_{\mathbf{G}_{0}}(\text{k};R))=R$
. To simplify the codomain, we have several cases.
$\operatorname{H}_{i}(\mathbf{G}_{0}(\text{k});\operatorname{St}_{\mathbf{G}_{0}}(\text{k};R))=R$
. To simplify the codomain, we have several cases.
–
 $\mathbf{G}_{1}=\operatorname{GL}_{1}$
or
$\mathbf{G}_{1}=\operatorname{GL}_{1}$
or
 $\mathbf{G}_{1}=\operatorname{SO}_{1,1}$
. In fact, these groups are isomorphic and are commutative, so
$\mathbf{G}_{1}=\operatorname{SO}_{1,1}$
. In fact, these groups are isomorphic and are commutative, so
 $\operatorname{St}_{\mathbf{G}_{1}}(\text{k};R)=R$
in these cases and (5.1) is an isomorphism.
$\operatorname{St}_{\mathbf{G}_{1}}(\text{k};R)=R$
in these cases and (5.1) is an isomorphism.–
 $\mathbf{G}_{1}=\operatorname{SL}_{1}$
. The group
$\mathbf{G}_{1}=\operatorname{SL}_{1}$
. The group
 $\operatorname{SL}_{1}$
is the trivial group and thus
$\operatorname{SL}_{1}$
is the trivial group and thus
 $\operatorname{St}_{\mathbf{G}_{1}}(\text{k};R)=R$
and (5.1) is an isomorphism.
$\operatorname{St}_{\mathbf{G}_{1}}(\text{k};R)=R$
and (5.1) is an isomorphism.–
 $\mathbf{G}_{1}=\operatorname{Sp}_{2}\cong \operatorname{SL}_{2}$
or
$\mathbf{G}_{1}=\operatorname{Sp}_{2}\cong \operatorname{SL}_{2}$
or
 $\mathbf{G}_{1}=\operatorname{SO}_{2,1}\cong \operatorname{PSL}_{2}$
. These groups have isomorphic Steinberg representations and the action of
$\mathbf{G}_{1}=\operatorname{SO}_{2,1}\cong \operatorname{PSL}_{2}$
. These groups have isomorphic Steinberg representations and the action of
 $\operatorname{SL}_{2}(\text{k})$
on
$\operatorname{SL}_{2}(\text{k})$
on
 $\operatorname{St}_{\operatorname{SL}_{2}}(\text{k};R)$
factors through
$\operatorname{St}_{\operatorname{SL}_{2}}(\text{k};R)$
factors through
 $\operatorname{PSL}_{2}(\text{k})$
. This case thus follows from Lemma 2.6, which says that
$\operatorname{PSL}_{2}(\text{k})$
. This case thus follows from Lemma 2.6, which says that
 $\operatorname{H}_{0}(\operatorname{SL}_{2}(\text{k});\operatorname{St}_{\operatorname{SL}_{2}}(\text{k};R))=0$
.
$\operatorname{H}_{0}(\operatorname{SL}_{2}(\text{k});\operatorname{St}_{\operatorname{SL}_{2}}(\text{k};R))=0$
.
This completes the base case.
Assume now that
![]() $i>0$
and that the desired result is true for all smaller values of
$i>0$
and that the desired result is true for all smaller values of
![]() $i$
. We will prove that the stabilization map
$i$
. We will prove that the stabilization map
is surjective for
![]() $n\geqslant 2i+1$
. Lemma 3.1 will then imply that
$n\geqslant 2i+1$
. Lemma 3.1 will then imply that
![]() $\operatorname{H}_{i}(\mathbf{G}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))=0$
for
$\operatorname{H}_{i}(\mathbf{G}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))=0$
for
![]() $n\geqslant 2i+2$
, and the theorem will follow.
$n\geqslant 2i+2$
, and the theorem will follow.
Fix some
![]() $n\geqslant 2i+1$
and let
$n\geqslant 2i+1$
and let
![]() $\text{k}^{m}$
be the standard vector space representation of
$\text{k}^{m}$
be the standard vector space representation of
![]() $\mathbf{G}_{n}(\text{k})$
(so
$\mathbf{G}_{n}(\text{k})$
(so
![]() $m$
is either
$m$
is either
![]() $n$
,
$n$
,
![]() $2n$
, or
$2n$
, or
![]() $2n+1$
). Let
$2n+1$
). Let
![]() $\{\vec{a}_{1},\ldots ,\vec{a}_{n}\}$
be the vectors in
$\{\vec{a}_{1},\ldots ,\vec{a}_{n}\}$
be the vectors in
![]() $\text{k}^{m}$
such that
$\text{k}^{m}$
such that
for
![]() $1\leqslant \ell \leqslant n$
. Combining the second conclusion of Theorem 5.4 with Lemma 5.1, we have a surjection
$1\leqslant \ell \leqslant n$
. Combining the second conclusion of Theorem 5.4 with Lemma 5.1, we have a surjection
We will analyze
![]() $\operatorname{H}_{i}^{\mathbf{G}_{n}(\text{k})}(\mathbf{CG}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))$
using the spectral sequence from Lemma 5.2. To calculate its
$\operatorname{H}_{i}^{\mathbf{G}_{n}(\text{k})}(\mathbf{CG}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))$
using the spectral sequence from Lemma 5.2. To calculate its
![]() $E^{1}$
-page, observe that the first conclusion of Theorem 5.4 says that
$E^{1}$
-page, observe that the first conclusion of Theorem 5.4 says that
![]() $\mathbf{G}_{n}(\text{k})$
acts transitively on the
$\mathbf{G}_{n}(\text{k})$
acts transitively on the
![]() $p$
-simplices of
$p$
-simplices of
![]() $\mathbf{CG}_{n}(\text{k})$
for
$\mathbf{CG}_{n}(\text{k})$
for
![]() $0\leqslant p<n-1$
. The stabilizer of the
$0\leqslant p<n-1$
. The stabilizer of the
![]() $(p-1)$
-simplex
$(p-1)$
-simplex
![]() $[\vec{a}_{1},\ldots ,\vec{a}_{p}]$
is
$[\vec{a}_{1},\ldots ,\vec{a}_{p}]$
is
![]() $\mathbf{FG}_{n}^{p}(\text{k})$
, so the spectral sequence in Lemma 5.2 has
$\mathbf{FG}_{n}^{p}(\text{k})$
, so the spectral sequence in Lemma 5.2 has
for
![]() $0\leqslant p<n-1$
.
$0\leqslant p<n-1$
.
We will prove that all of the terms on the
![]() $p+q=i$
line of the
$p+q=i$
line of the
![]() $E^{\infty }$
-page of our spectral sequence vanish except for possibly the term
$E^{\infty }$
-page of our spectral sequence vanish except for possibly the term
![]() $E_{0,i}^{\infty }$
. To do this, consider
$E_{0,i}^{\infty }$
. To do this, consider
![]() $p,q\geqslant 0$
with
$p,q\geqslant 0$
with
![]() $p+q=i$
and
$p+q=i$
and
![]() $p\geqslant 1$
. The case
$p\geqslant 1$
. The case
![]() $p=1$
and
$p=1$
and
![]() $n=2i+1$
is exceptional and must be treated separately. To avoid getting bogged down here, we postpone this calculation until § 6 below, where it appears as Lemma 6.1.Footnote
1
$n=2i+1$
is exceptional and must be treated separately. To avoid getting bogged down here, we postpone this calculation until § 6 below, where it appears as Lemma 6.1.Footnote
1
We thus can assume that either
![]() $p\geqslant 2$
or that
$p\geqslant 2$
or that
![]() $n\geqslant 2i+2$
. Since
$n\geqslant 2i+2$
. Since
![]() $n\geqslant 2i+1$
, we certainly have
$n\geqslant 2i+1$
, we certainly have
![]() $p<n-1$
, so
$p<n-1$
, so
![]() $E_{p,q}^{1}$
is in the regime where the above description of the
$E_{p,q}^{1}$
is in the regime where the above description of the
![]() $E^{1}$
-page holds. Applying Corollary 4.2 to (5.4), we see that
$E^{1}$
-page holds. Applying Corollary 4.2 to (5.4), we see that
To see that this vanishes, it is enough to show that
![]() $\operatorname{H}_{q}(\mathbf{G}_{n-p-1}(\text{k});\operatorname{St}_{\mathbf{G}_{n-p-1}}(\text{k};R))=0$
. This is a consequence of our inductive hypothesis; to see that it applies, observe that if
$\operatorname{H}_{q}(\mathbf{G}_{n-p-1}(\text{k});\operatorname{St}_{\mathbf{G}_{n-p-1}}(\text{k};R))=0$
. This is a consequence of our inductive hypothesis; to see that it applies, observe that if
![]() $p\geqslant 2$
then
$p\geqslant 2$
then
while if
![]() $p=1$
and
$p=1$
and
![]() $n\geqslant 2i+2$
then
$n\geqslant 2i+2$
then
This implies that
![]() $E_{p,q}^{1}=0$
, and thus that
$E_{p,q}^{1}=0$
, and thus that
![]() $E_{p,q}^{\infty }=0$
.
$E_{p,q}^{\infty }=0$
.
The
![]() $p+q=i$
line of the
$p+q=i$
line of the
![]() $E^{\infty }$
-page of our spectral sequence thus only has a single potentially nonzero entry, namely
$E^{\infty }$
-page of our spectral sequence thus only has a single potentially nonzero entry, namely
![]() $E_{0,i}^{\infty }$
, and this is a quotient of
$E_{0,i}^{\infty }$
, and this is a quotient of
This entry thus surjects onto
![]() $\operatorname{H}_{i}^{\mathbf{G}_{n}(\text{k})}(\mathbf{CG}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))$
. Combining this with the surjection (5.3), we obtain a surjection
$\operatorname{H}_{i}^{\mathbf{G}_{n}(\text{k})}(\mathbf{CG}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))$
. Combining this with the surjection (5.3), we obtain a surjection
Examining the construction of our spectral sequence in [Reference BrownBro94, ch. VII.7], it is easy to see that this comes from the map induced by the inclusion
![]() $\mathbf{FG}_{n}^{1}(\text{k}){\hookrightarrow}\mathbf{G}_{n}(\text{k})$
. Combining (5.5) with the isomorphism
$\mathbf{FG}_{n}^{1}(\text{k}){\hookrightarrow}\mathbf{G}_{n}(\text{k})$
. Combining (5.5) with the isomorphism
given by the
![]() $\ell =1$
case of Corollary 4.2, we conclude that (5.2) is a surjection, as desired.
$\ell =1$
case of Corollary 4.2, we conclude that (5.2) is a surjection, as desired.
6 Killing the exceptional term in the spectral sequence
This section is devoted to proving the vanishing result postponed from the proof of Theorem 1.1 in § 5.3. The notation in this section is thus identical to that in § 5.3:
–
 $\mathbf{G}_{n}$
is either
$\mathbf{G}_{n}$
is either
 $\operatorname{GL}_{n}$
,
$\operatorname{GL}_{n}$
,
 $\operatorname{SL}_{n}$
,
$\operatorname{SL}_{n}$
,
 $\operatorname{Sp}_{2n}$
,
$\operatorname{Sp}_{2n}$
,
 $\operatorname{SO}_{n,n}$
, or
$\operatorname{SO}_{n,n}$
, or
 $\operatorname{SO}_{n,n+1}$
;
$\operatorname{SO}_{n,n+1}$
;–
 $\text{k}$
is a field and
$\text{k}$
is a field and
 $R$
is a commutative ring;
$R$
is a commutative ring;–
 $i>0$
and
$i>0$
and
 $n=2i+1$
(the only case that remained in that section);
$n=2i+1$
(the only case that remained in that section);–
 $\text{k}^{m}$
is the standard vector space representation of
$\text{k}^{m}$
is the standard vector space representation of
 $\mathbf{G}_{n}(\text{k})$
(so
$\mathbf{G}_{n}(\text{k})$
(so
 $m$
is either
$m$
is either
 $n$
,
$n$
,
 $2n$
, or
$2n$
, or
 $2n+1$
);
$2n+1$
);–
 $\{\vec{a}_{1},\ldots ,\vec{a}_{n}\}$
is the set of vectors in
$\{\vec{a}_{1},\ldots ,\vec{a}_{n}\}$
is the set of vectors in
 $\text{k}^{m}$
such that for
$\text{k}^{m}$
such that for $$\begin{eqnarray}\mathbf{FG}_{n}^{\ell }(\text{k})=\{M\in \mathbf{G}_{n}(\text{k})\mid M(\vec{a}_{j})=\vec{a}_{j}\text{ for }1\leqslant j\leqslant \ell \}\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{FG}_{n}^{\ell }(\text{k})=\{M\in \mathbf{G}_{n}(\text{k})\mid M(\vec{a}_{j})=\vec{a}_{j}\text{ for }1\leqslant j\leqslant \ell \}\end{eqnarray}$$
 $1\leqslant \ell \leqslant n$
.
$1\leqslant \ell \leqslant n$
.–
 $E_{p,q}^{r}$
is the spectral sequence from Lemma 5.2 converging to
$E_{p,q}^{r}$
is the spectral sequence from Lemma 5.2 converging to
 $\operatorname{H}_{i}^{\mathbf{G}_{n}(\text{k})}(\mathbf{CG}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))$
.
$\operatorname{H}_{i}^{\mathbf{G}_{n}(\text{k})}(\mathbf{CG}_{n}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))$
.
What we must prove is as follows.
Lemma 6.1. Let the notation be as above, and assume that the stabilization map
is surjective. Then the differential
![]() $E_{2,i-1}^{1}\rightarrow E_{1,i-1}^{1}$
is surjective, and thus
$E_{2,i-1}^{1}\rightarrow E_{1,i-1}^{1}$
is surjective, and thus
![]() $E_{1,i-1}^{\infty }=0$
.
$E_{1,i-1}^{\infty }=0$
.
The proof of Lemma 6.1 is divided into five sections.
– In § 6.1, we give an explicit form for the differential
 $E_{2,i-1}^{1}\rightarrow E_{1,i-1}^{1}$
.
$E_{2,i-1}^{1}\rightarrow E_{1,i-1}^{1}$
.– In § 6.2, we translate that explicit form into one involving the stabilization map (6.1).
– In § 6.3, we summarize what remains to be proved.
– In § 6.4, we give some needed background information about apartments.
6.1 Identifying the differential
The notation is as in the beginning of § 6. In this section, we identify the differential
![]() $E_{2,i-1}^{1}\rightarrow E_{1,i-1}^{1}$
. Since
$E_{2,i-1}^{1}\rightarrow E_{1,i-1}^{1}$
. Since
![]() $n=2i+1$
and
$n=2i+1$
and
![]() $i>0$
, we have
$i>0$
, we have
![]() $1<n-1$
, so
$1<n-1$
, so
![]() $E_{1,i-1}^{1}$
is as described in (5.4), i.e.
$E_{1,i-1}^{1}$
is as described in (5.4), i.e.
If
![]() $i=1$
, then we do not have
$i=1$
, then we do not have
![]() $2<n-1$
, so in this case
$2<n-1$
, so in this case
![]() $E_{2,i-1}^{1}$
is not as described in (5.4). The issue is that
$E_{2,i-1}^{1}$
is not as described in (5.4). The issue is that
![]() $\mathbf{G}_{n}(\text{k})$
might not act transitively on the
$\mathbf{G}_{n}(\text{k})$
might not act transitively on the
![]() $2$
-simplices of
$2$
-simplices of
![]() $\mathbf{CG}_{n}(\text{k})$
(this is actually only a problem for
$\mathbf{CG}_{n}(\text{k})$
(this is actually only a problem for
![]() $\mathbf{G}_{n}=\operatorname{SL}_{n}$
). However, for all values of
$\mathbf{G}_{n}=\operatorname{SL}_{n}$
). However, for all values of
![]() $i$
it is still the case that
$i$
it is still the case that
![]() $E_{2,i-1}^{1}$
contains
$E_{2,i-1}^{1}$
contains
as a summand. The restriction of the differential
![]() $E_{2,i-1}^{1}\rightarrow E_{1,i-1}^{1}$
to this summand is a map
$E_{2,i-1}^{1}\rightarrow E_{1,i-1}^{1}$
to this summand is a map
To prove Lemma 6.1, it is enough to prove that
![]() $\unicode[STIX]{x2202}$
is surjective.
$\unicode[STIX]{x2202}$
is surjective.
We can describe
![]() $\unicode[STIX]{x2202}$
using the recipe described in [Reference BrownBro94, ch. VII.8]. Recall that
$\unicode[STIX]{x2202}$
using the recipe described in [Reference BrownBro94, ch. VII.8]. Recall that
![]() $\mathbf{FG}_{n}^{3}(\text{k})$
is the
$\mathbf{FG}_{n}^{3}(\text{k})$
is the
![]() $\mathbf{G}_{n}(\text{k})$
-stabilizer of the ordered sequence of vectors
$\mathbf{G}_{n}(\text{k})$
-stabilizer of the ordered sequence of vectors
![]() $\unicode[STIX]{x1D70E}=[\vec{a}_{1},\vec{a}_{2},\vec{a}_{3}]$
. For
$\unicode[STIX]{x1D70E}=[\vec{a}_{1},\vec{a}_{2},\vec{a}_{3}]$
. For
![]() $1\leqslant m\leqslant 3$
, let
$1\leqslant m\leqslant 3$
, let
![]() $\unicode[STIX]{x1D70E}_{m}$
be the ordered sequence obtained by deleting
$\unicode[STIX]{x1D70E}_{m}$
be the ordered sequence obtained by deleting
![]() $\vec{a}_{m}$
from
$\vec{a}_{m}$
from
![]() $\unicode[STIX]{x1D70E}$
and let
$\unicode[STIX]{x1D70E}$
and let
![]() $(\mathbf{G}_{n}(k))_{\unicode[STIX]{x1D70E}_{m}}$
denote the
$(\mathbf{G}_{n}(k))_{\unicode[STIX]{x1D70E}_{m}}$
denote the
![]() $\mathbf{G}_{n}(k)$
-stabilizer of
$\mathbf{G}_{n}(k)$
-stabilizer of
![]() $\unicode[STIX]{x1D70E}_{m}$
. We then have
$\unicode[STIX]{x1D70E}_{m}$
. We then have
![]() $\unicode[STIX]{x2202}=\unicode[STIX]{x2202}_{1}-\unicode[STIX]{x2202}_{2}+\unicode[STIX]{x2202}_{3}$
, where
$\unicode[STIX]{x2202}=\unicode[STIX]{x2202}_{1}-\unicode[STIX]{x2202}_{2}+\unicode[STIX]{x2202}_{3}$
, where
![]() $\unicode[STIX]{x2202}_{m}$
is the composition
$\unicode[STIX]{x2202}_{m}$
is the composition
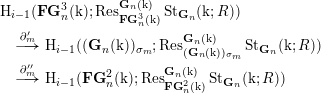 $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{H}_{i-1}(\mathbf{FG}_{n}^{3}(\text{k});\operatorname{Res}_{\mathbf{FG}_{n}^{3}(\text{k})}^{\mathbf{G}_{n}(\text{k})}\operatorname{St}_{\boldsymbol{ G}_{n}}(\text{k};R))\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\unicode[STIX]{x2202}_{m}^{\prime }}{\longrightarrow }\operatorname{H}_{i-1}((\mathbf{G}_{n}(\text{k}))_{\unicode[STIX]{x1D70E}_{m}};\operatorname{Res}_{(\mathbf{G}_{n}(\text{k}))_{\unicode[STIX]{x1D70E}_{m}}}^{\mathbf{G}_{n}(\text{k})}\operatorname{St}_{\boldsymbol{ G}_{n}}(\text{k};R))\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\unicode[STIX]{x2202}_{m}^{\prime \prime }}{\longrightarrow }\operatorname{H}_{i-1}(\mathbf{FG}_{n}^{2}(\text{k});\operatorname{Res}_{\mathbf{FG}_{n}^{2}(\text{k})}^{\mathbf{G}_{n}(\text{k})}\operatorname{St}_{\boldsymbol{ G}_{n}}(\text{k};R))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{H}_{i-1}(\mathbf{FG}_{n}^{3}(\text{k});\operatorname{Res}_{\mathbf{FG}_{n}^{3}(\text{k})}^{\mathbf{G}_{n}(\text{k})}\operatorname{St}_{\boldsymbol{ G}_{n}}(\text{k};R))\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\unicode[STIX]{x2202}_{m}^{\prime }}{\longrightarrow }\operatorname{H}_{i-1}((\mathbf{G}_{n}(\text{k}))_{\unicode[STIX]{x1D70E}_{m}};\operatorname{Res}_{(\mathbf{G}_{n}(\text{k}))_{\unicode[STIX]{x1D70E}_{m}}}^{\mathbf{G}_{n}(\text{k})}\operatorname{St}_{\boldsymbol{ G}_{n}}(\text{k};R))\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\unicode[STIX]{x2202}_{m}^{\prime \prime }}{\longrightarrow }\operatorname{H}_{i-1}(\mathbf{FG}_{n}^{2}(\text{k});\operatorname{Res}_{\mathbf{FG}_{n}^{2}(\text{k})}^{\mathbf{G}_{n}(\text{k})}\operatorname{St}_{\boldsymbol{ G}_{n}}(\text{k};R))\nonumber\end{eqnarray}$$
of the following two maps.
– The map
 $\unicode[STIX]{x2202}_{m}^{\prime }$
is induced by the inclusion
$\unicode[STIX]{x2202}_{m}^{\prime }$
is induced by the inclusion
 $\mathbf{FG}_{n}^{3}(\text{k}){\hookrightarrow}(\mathbf{G}_{n}(\text{k}))_{\unicode[STIX]{x1D70E}_{m}}$
.
$\mathbf{FG}_{n}^{3}(\text{k}){\hookrightarrow}(\mathbf{G}_{n}(\text{k}))_{\unicode[STIX]{x1D70E}_{m}}$
.– Define
 $\unicode[STIX]{x1D705}_{m}\in \mathbf{G}_{n}(\text{k})$
as follows. First,
$\unicode[STIX]{x1D705}_{m}\in \mathbf{G}_{n}(\text{k})$
as follows. First,
 $\unicode[STIX]{x1D705}_{3}=\text{id}$
. For
$\unicode[STIX]{x1D705}_{3}=\text{id}$
. For
 $m\in \{1,2\}$
, we do the following.
$m\in \{1,2\}$
, we do the following.* If
 $\mathbf{G}_{n}=\operatorname{GL}_{n}$
or
$\mathbf{G}_{n}=\operatorname{GL}_{n}$
or
 $\mathbf{G}_{n}=\operatorname{SL}_{n}$
, then
$\mathbf{G}_{n}=\operatorname{SL}_{n}$
, then
 $\unicode[STIX]{x1D705}_{m}\in \operatorname{SL}_{n}(\text{k})$
is the map
$\unicode[STIX]{x1D705}_{m}\in \operatorname{SL}_{n}(\text{k})$
is the map
 $\text{k}^{n}\rightarrow \text{k}^{n}$
that takes
$\text{k}^{n}\rightarrow \text{k}^{n}$
that takes
 $\vec{a}_{m}$
to
$\vec{a}_{m}$
to
 $\vec{a}_{3}$
, takes
$\vec{a}_{3}$
, takes
 $\vec{a}_{3}$
to
$\vec{a}_{3}$
to
 $-\vec{a}_{m}$
, and fixes all the other basis vectors.
$-\vec{a}_{m}$
, and fixes all the other basis vectors.* If
 $\mathbf{G}_{n}=\operatorname{Sp}_{2n}$
or
$\mathbf{G}_{n}=\operatorname{Sp}_{2n}$
or
 $\mathbf{G}_{n}=\operatorname{SO}_{n,n}$
or
$\mathbf{G}_{n}=\operatorname{SO}_{n,n}$
or
 $\mathbf{G}_{n}=\operatorname{SO}_{n,n+1}$
, then
$\mathbf{G}_{n}=\operatorname{SO}_{n,n+1}$
, then
 $\unicode[STIX]{x1D705}_{m}\in \mathbf{G}_{n}(\text{k})$
is the map
$\unicode[STIX]{x1D705}_{m}\in \mathbf{G}_{n}(\text{k})$
is the map
 $\text{k}^{m}\rightarrow \text{k}^{m}$
defined as follows. Let
$\text{k}^{m}\rightarrow \text{k}^{m}$
defined as follows. Let
 $\vec{b}_{1},\ldots ,\vec{b}_{n}$
be the standard basis vectors for
$\vec{b}_{1},\ldots ,\vec{b}_{n}$
be the standard basis vectors for
 $\text{k}^{m}$
that pair with the
$\text{k}^{m}$
that pair with the
 $\vec{a}_{j}$
(there is one additional standard basis vector if
$\vec{a}_{j}$
(there is one additional standard basis vector if
 $\mathbf{G}_{n}=\operatorname{SO}_{n,n+1}$
). Then
$\mathbf{G}_{n}=\operatorname{SO}_{n,n+1}$
). Then
 $\unicode[STIX]{x1D705}_{m}$
takes
$\unicode[STIX]{x1D705}_{m}$
takes
 $\vec{a}_{m}$
to
$\vec{a}_{m}$
to
 $\vec{a}_{3}$
, takes
$\vec{a}_{3}$
, takes
 $\vec{a}_{3}$
to
$\vec{a}_{3}$
to
 $-\vec{a}_{m}$
, takes
$-\vec{a}_{m}$
, takes
 $\vec{b}_{m}$
to
$\vec{b}_{m}$
to
 $\vec{b}_{3}$
, takes
$\vec{b}_{3}$
, takes
 $\vec{b}_{3}$
to
$\vec{b}_{3}$
to
 $-\vec{b}_{m}$
, and fixes all the other basis vectors.
$-\vec{b}_{m}$
, and fixes all the other basis vectors.
Then
 $\unicode[STIX]{x2202}_{m}^{\prime \prime }$
is induced by the map
$\unicode[STIX]{x2202}_{m}^{\prime \prime }$
is induced by the map
 $(\mathbf{G}_{n}(\text{k}))_{\unicode[STIX]{x1D70E}_{m}}\rightarrow \mathbf{FG}_{n}^{2}(\text{k})$
that takes
$(\mathbf{G}_{n}(\text{k}))_{\unicode[STIX]{x1D70E}_{m}}\rightarrow \mathbf{FG}_{n}^{2}(\text{k})$
that takes
 $g\in (\mathbf{G}_{n}(\text{k}))_{\unicode[STIX]{x1D70E}_{m}}$
to
$g\in (\mathbf{G}_{n}(\text{k}))_{\unicode[STIX]{x1D70E}_{m}}$
to
 $\unicode[STIX]{x1D705}_{m}g\unicode[STIX]{x1D705}_{m}^{-1}$
and the map
$\unicode[STIX]{x1D705}_{m}g\unicode[STIX]{x1D705}_{m}^{-1}$
and the map
 $\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
that takes
$\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
that takes
 $x\in \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
to
$x\in \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
to
 $\unicode[STIX]{x1D705}_{m}(x)\in \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
. We remark that easier choices of
$\unicode[STIX]{x1D705}_{m}(x)\in \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
. We remark that easier choices of
 $\unicode[STIX]{x1D705}_{m}$
(without the signs) could be used for
$\unicode[STIX]{x1D705}_{m}$
(without the signs) could be used for
 $\mathbf{G}_{n}\neq \operatorname{SL}_{n}$
, but we chose the ones above to make our later formulas more uniform.
$\mathbf{G}_{n}\neq \operatorname{SL}_{n}$
, but we chose the ones above to make our later formulas more uniform.
This is summarized in the following lemma.
Lemma 6.2. Let the notation be as above. Then the map
![]() $\unicode[STIX]{x2202}$
in (6.2) equals
$\unicode[STIX]{x2202}$
in (6.2) equals
![]() $\unicode[STIX]{x2202}_{1}-\unicode[STIX]{x2202}_{2}+\unicode[STIX]{x2202}_{3}$
, where
$\unicode[STIX]{x2202}_{1}-\unicode[STIX]{x2202}_{2}+\unicode[STIX]{x2202}_{3}$
, where
![]() $\unicode[STIX]{x2202}_{m}$
is induced by the map
$\unicode[STIX]{x2202}_{m}$
is induced by the map
![]() $\mathbf{FG}_{n}^{3}(\text{k})\rightarrow \mathbf{FG}_{n}^{2}(\text{k})$
defined via the formula
$\mathbf{FG}_{n}^{3}(\text{k})\rightarrow \mathbf{FG}_{n}^{2}(\text{k})$
defined via the formula
and the map
![]() $\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
defined via the formula
$\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
defined via the formula
6.2 Bringing in the stabilization map
The notation is as in the beginning of § 6. Fix some
![]() $1\leqslant m\leqslant 3$
, and let
$1\leqslant m\leqslant 3$
, and let
![]() $\unicode[STIX]{x2202}_{m}$
and
$\unicode[STIX]{x2202}_{m}$
and
![]() $\unicode[STIX]{x1D705}_{m}$
be as in Lemma 6.2. Applying the isomorphism in Corollary 4.2 to the domain and codomain of
$\unicode[STIX]{x1D705}_{m}$
be as in Lemma 6.2. Applying the isomorphism in Corollary 4.2 to the domain and codomain of
![]() $\unicode[STIX]{x2202}_{m}$
, we obtain a homomorphism
$\unicode[STIX]{x2202}_{m}$
, we obtain a homomorphism
Our goal in this section is to prove that
![]() $\widehat{\unicode[STIX]{x2202}}_{m}$
is the tensor product of the stabilization map
$\widehat{\unicode[STIX]{x2202}}_{m}$
is the tensor product of the stabilization map
with the map
![]() $\unicode[STIX]{x1D701}_{m}:\operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)\rightarrow \operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)$
defined as follows. Let
$\unicode[STIX]{x1D701}_{m}:\operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)\rightarrow \operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)$
defined as follows. Let
![]() $\{\vec{a}_{1},\vec{a}_{2},\vec{a}_{3}\}$
be the standard basis for
$\{\vec{a}_{1},\vec{a}_{2},\vec{a}_{3}\}$
be the standard basis for
![]() $\text{k}^{3}$
. Let
$\text{k}^{3}$
. Let
![]() $\widehat{\unicode[STIX]{x1D705}}_{3}=\text{id}\in \operatorname{SL}_{3}(\text{k})$
, and for
$\widehat{\unicode[STIX]{x1D705}}_{3}=\text{id}\in \operatorname{SL}_{3}(\text{k})$
, and for
![]() $m\in \{1,2\}$
let
$m\in \{1,2\}$
let
![]() $\widehat{\unicode[STIX]{x1D705}}_{m}\in \operatorname{SL}_{3}(\text{k})$
be the element that takes
$\widehat{\unicode[STIX]{x1D705}}_{m}\in \operatorname{SL}_{3}(\text{k})$
be the element that takes
![]() $\vec{a}_{m}$
to
$\vec{a}_{m}$
to
![]() $\vec{a}_{3}$
, takes
$\vec{a}_{3}$
, takes
![]() $\vec{a}_{3}$
to
$\vec{a}_{3}$
to
![]() $-\vec{a}_{m}$
, and fixes all the other basis vectors. Then
$-\vec{a}_{m}$
, and fixes all the other basis vectors. Then
![]() $\unicode[STIX]{x1D701}_{m}$
is the composition
$\unicode[STIX]{x1D701}_{m}$
is the composition
where the second arrow is the Reeder projection map (see § 4) and the final isomorphism comes from the fact that
![]() $\operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)=R$
.
$\operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)=R$
.
The main result of this section is then as follows.
Lemma 6.3. Let the notation be as above. Then
![]() $\widehat{\unicode[STIX]{x2202}}_{m}$
is the tensor product of
$\widehat{\unicode[STIX]{x2202}}_{m}$
is the tensor product of
![]() $\unicode[STIX]{x1D701}_{m}$
with the stabilization map (6.3).
$\unicode[STIX]{x1D701}_{m}$
with the stabilization map (6.3).
Proof. By construction,
![]() $\widehat{\unicode[STIX]{x2202}}_{m}$
equals the composition
$\widehat{\unicode[STIX]{x2202}}_{m}$
equals the composition
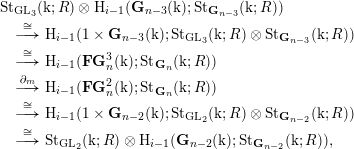 $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)\otimes \operatorname{H}_{i-1}(\mathbf{G}_{n-3}(\text{k});\operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R))\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\cong }{\longrightarrow }\operatorname{H}_{i-1}(1\times \mathbf{G}_{n-3}(\text{k});\operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R))\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\cong }{\longrightarrow }\operatorname{H}_{i-1}(\mathbf{FG}_{n}^{3}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\unicode[STIX]{x2202}_{m}}{\longrightarrow }\operatorname{H}_{i-1}(\mathbf{FG}_{n}^{2}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\cong }{\longrightarrow }\operatorname{H}_{i-1}(1\times \mathbf{G}_{n-2}(\text{k});\operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-2}}(\text{k};R))\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\cong }{\longrightarrow }\operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)\otimes \operatorname{H}_{i-1}(\mathbf{G}_{n-2}(\text{k});\operatorname{St}_{\mathbf{G}_{n-2}}(\text{k};R)),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)\otimes \operatorname{H}_{i-1}(\mathbf{G}_{n-3}(\text{k});\operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R))\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\cong }{\longrightarrow }\operatorname{H}_{i-1}(1\times \mathbf{G}_{n-3}(\text{k});\operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R))\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\cong }{\longrightarrow }\operatorname{H}_{i-1}(\mathbf{FG}_{n}^{3}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\unicode[STIX]{x2202}_{m}}{\longrightarrow }\operatorname{H}_{i-1}(\mathbf{FG}_{n}^{2}(\text{k});\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R))\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\cong }{\longrightarrow }\operatorname{H}_{i-1}(1\times \mathbf{G}_{n-2}(\text{k});\operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-2}}(\text{k};R))\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\cong }{\longrightarrow }\operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)\otimes \operatorname{H}_{i-1}(\mathbf{G}_{n-2}(\text{k});\operatorname{St}_{\mathbf{G}_{n-2}}(\text{k};R)),\nonumber\end{eqnarray}$$
where the various maps are as follows.
– The first and last arrows use the fact that
 $\operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)$
and
$\operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)$
and
 $\operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)$
are free
$\operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)$
are free
 $R$
-modules (cf. the proof of Corollary 4.2).
$R$
-modules (cf. the proof of Corollary 4.2).– The second arrow is the map described in Lemma 4.1, that is, the map induced by the inclusion
 $1\times \mathbf{G}_{n-3}(\text{k}){\hookrightarrow}\mathbf{FG}_{n}^{3}(\text{k})$
and the Reeder product map
$1\times \mathbf{G}_{n-3}(\text{k}){\hookrightarrow}\mathbf{FG}_{n}^{3}(\text{k})$
and the Reeder product map
 $\operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
.
$\operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
.– The third arrow is the map
 $\unicode[STIX]{x2202}_{m}$
described in Lemma 6.2, that is, the map induced by the map
$\unicode[STIX]{x2202}_{m}$
described in Lemma 6.2, that is, the map induced by the map
 $\mathbf{FG}_{n}^{3}(\text{k})\rightarrow \mathbf{FG}_{n}^{2}(\text{k})$
given by conjugation by
$\mathbf{FG}_{n}^{3}(\text{k})\rightarrow \mathbf{FG}_{n}^{2}(\text{k})$
given by conjugation by
 $\unicode[STIX]{x1D705}_{m}$
and the map
$\unicode[STIX]{x1D705}_{m}$
and the map
 $\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
induced by
$\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)$
induced by
 $\unicode[STIX]{x1D705}_{m}$
.
$\unicode[STIX]{x1D705}_{m}$
.– The fourth arrow is the map described in Lemma 4.3, that is, the map induced by the projection
 $\mathbf{FG}_{n}^{2}(\text{k})\rightarrow 1\times \mathbf{G}_{n-2}(\text{k})$
together with the Reeder projection map
$\mathbf{FG}_{n}^{2}(\text{k})\rightarrow 1\times \mathbf{G}_{n-2}(\text{k})$
together with the Reeder projection map
 $\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)\rightarrow \operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-2}}(\text{k};R)$
.
$\operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)\rightarrow \operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-2}}(\text{k};R)$
.
We must show that this composition equals the indicated tensor product of maps. This will take some work.
Define
![]() $\unicode[STIX]{x1D6F9}$
to be the composition
$\unicode[STIX]{x1D6F9}$
to be the composition
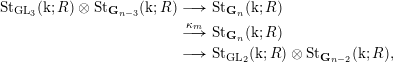 $$\begin{eqnarray}\displaystyle \operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R) & \longrightarrow & \displaystyle \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)\nonumber\\ \displaystyle & \stackrel{\unicode[STIX]{x1D705}_{m}}{\longrightarrow } & \displaystyle \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)\nonumber\\ \displaystyle & \longrightarrow & \displaystyle \operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-2}}(\text{k};R),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R) & \longrightarrow & \displaystyle \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)\nonumber\\ \displaystyle & \stackrel{\unicode[STIX]{x1D705}_{m}}{\longrightarrow } & \displaystyle \operatorname{St}_{\mathbf{G}_{n}}(\text{k};R)\nonumber\\ \displaystyle & \longrightarrow & \displaystyle \operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-2}}(\text{k};R),\nonumber\end{eqnarray}$$
where the first map is the Reeder product map and the last map is the Reeder projection map. Also, define
![]() $\unicode[STIX]{x1D6F7}$
to be the composition
$\unicode[STIX]{x1D6F7}$
to be the composition
where the maps are as follows.
– The first map is the tensor product of the Reeder projection map
 $\operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)\rightarrow \operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)\otimes \operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)$
and the identity map
$\operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)\rightarrow \operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)\otimes \operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)$
and the identity map
 $\operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R)$
.
$\operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R)$
.– The second map is the tensor product of the identity map
 $\operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)\rightarrow \operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)$
and the Reeder product map
$\operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)\rightarrow \operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)$
and the Reeder product map
 $\operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n-2}}(\text{k};R)$
.
$\operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R)\rightarrow \operatorname{St}_{\mathbf{G}_{n-2}}(\text{k};R)$
.
By the above, it is enough to prove that
![]() $\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D6F7}\circ (\widehat{\unicode[STIX]{x1D705}}_{m}\otimes \text{id})$
.
$\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D6F7}\circ (\widehat{\unicode[STIX]{x1D705}}_{m}\otimes \text{id})$
.
Define
![]() $\unicode[STIX]{x1D6F9}^{\prime }$
to be the composition
$\unicode[STIX]{x1D6F9}^{\prime }$
to be the composition
where the first map is the Reeder product map and the second map is the Reeder projection map. From its definition, we see that
![]() $\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D6F9}^{\prime }\circ (\widehat{\unicode[STIX]{x1D705}}_{m}\otimes \text{id})$
. We thus see that it is enough to prove that
$\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D6F9}^{\prime }\circ (\widehat{\unicode[STIX]{x1D705}}_{m}\otimes \text{id})$
. We thus see that it is enough to prove that
![]() $\unicode[STIX]{x1D6F9}^{\prime }=\unicode[STIX]{x1D6F7}$
.
$\unicode[STIX]{x1D6F9}^{\prime }=\unicode[STIX]{x1D6F7}$
.
Define
![]() $U=\mathbf{UGL}_{3}^{2}(\text{k})$
to be the unipotent radical of the parabolic subgroup
$U=\mathbf{UGL}_{3}^{2}(\text{k})$
to be the unipotent radical of the parabolic subgroup
![]() $\mathbf{PGL}_{3}^{2}(\text{k})$
of
$\mathbf{PGL}_{3}^{2}(\text{k})$
of
![]() $\operatorname{GL}_{3}(\text{k})$
(despite the bad notation, this is not the projective general linear group). Using Theorem 2.1 as in Remark 2.5, we see that
$\operatorname{GL}_{3}(\text{k})$
(despite the bad notation, this is not the projective general linear group). Using Theorem 2.1 as in Remark 2.5, we see that
Consider
![]() $u\in U$
and
$u\in U$
and
![]() $x\in \operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)$
and
$x\in \operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)$
and
![]() $y\in \operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)$
and
$y\in \operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)$
and
![]() $z\in \operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R)$
. Examining the definition of
$z\in \operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R)$
. Examining the definition of
![]() $\unicode[STIX]{x1D6F9}^{\prime }$
, we see that
$\unicode[STIX]{x1D6F9}^{\prime }$
, we see that
where
![]() $y\otimes z\in \operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R)$
is identified with an element of
$y\otimes z\in \operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)\otimes \operatorname{St}_{\mathbf{G}_{n-3}}(\text{k};R)$
is identified with an element of
![]() $\operatorname{St}_{\mathbf{G}_{n-2}}(\text{k};R)$
using the Reeder product map. But this equals
$\operatorname{St}_{\mathbf{G}_{n-2}}(\text{k};R)$
using the Reeder product map. But this equals
![]() $\unicode[STIX]{x1D6F7}((u\cdot (x\otimes y))\otimes z)$
, as desired.◻
$\unicode[STIX]{x1D6F7}((u\cdot (x\otimes y))\otimes z)$
, as desired.◻
6.3 Summary of where we are
The notation is as in the beginning of § 6. Recall that Lemma 6.1 asserts that the differential
![]() $E_{2,i-1}^{1}\rightarrow E_{1,i-1}^{1}$
is surjective. Let
$E_{2,i-1}^{1}\rightarrow E_{1,i-1}^{1}$
is surjective. Let
![]() $\unicode[STIX]{x2202}$
be as in § 6.1. Also, let
$\unicode[STIX]{x2202}$
be as in § 6.1. Also, let
![]() $\unicode[STIX]{x1D701}_{m}$
and
$\unicode[STIX]{x1D701}_{m}$
and
![]() $\widehat{\unicode[STIX]{x1D705}}_{m}$
be as in § 6.2. Define
$\widehat{\unicode[STIX]{x1D705}}_{m}$
be as in § 6.2. Define
via the formula
![]() $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D701}_{1}-\unicode[STIX]{x1D701}_{2}+\unicode[STIX]{x1D701}_{3}$
. Combining Lemmas 6.2 and 6.3, we see that to prove Lemma 6.1, it is enough to show that the map
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D701}_{1}-\unicode[STIX]{x1D701}_{2}+\unicode[STIX]{x1D701}_{3}$
. Combining Lemmas 6.2 and 6.3, we see that to prove Lemma 6.1, it is enough to show that the map
obtained as the tensor product of
![]() $\unicode[STIX]{x1D701}$
and the stabilization map
$\unicode[STIX]{x1D701}$
and the stabilization map
is surjective. One of the assumptions in Lemma 6.1 is that this stabilization map is surjective. To prove that lemma, it is thus enough to prove the following.
Lemma 6.4. Let the notation be as above. Then
![]() $\unicode[STIX]{x1D701}$
is surjective.
$\unicode[STIX]{x1D701}$
is surjective.
6.4 Apartments
Before we prove Lemma 6.4, we need to discuss some background material on the Steinberg representation. Unlike the previous sections, in this section
![]() $n\geqslant 1$
is arbitrary. Recall that
$n\geqslant 1$
is arbitrary. Recall that
![]() $\operatorname{St}_{\operatorname{GL}_{n}}(\text{k};R)=\widetilde{\operatorname{H}}_{n-2}({\mathcal{T}}_{\operatorname{GL}_{n}}(\text{k});R)$
, where
$\operatorname{St}_{\operatorname{GL}_{n}}(\text{k};R)=\widetilde{\operatorname{H}}_{n-2}({\mathcal{T}}_{\operatorname{GL}_{n}}(\text{k});R)$
, where
![]() ${\mathcal{T}}_{\operatorname{GL}_{n}}(\text{k})$
is the Tits building associated to
${\mathcal{T}}_{\operatorname{GL}_{n}}(\text{k})$
is the Tits building associated to
![]() $\operatorname{GL}_{n}(\text{k})$
. This building can be described as the simplicial complex whose
$\operatorname{GL}_{n}(\text{k})$
. This building can be described as the simplicial complex whose
![]() $r$
-simplices are flags
$r$
-simplices are flags
of nonzero proper subspaces of
![]() $\text{k}^{n}$
.
$\text{k}^{n}$
.
The Solomon–Tits theorem [Reference BrownBro89, Theorem IV.5.2] says that the
![]() $R$
-module
$R$
-module
![]() $\operatorname{St}_{\operatorname{GL}_{n}}(\text{k};R)$
is spanned by apartment classes, which are defined as follows. Consider an
$\operatorname{St}_{\operatorname{GL}_{n}}(\text{k};R)$
is spanned by apartment classes, which are defined as follows. Consider an
![]() $n\times n$
matrix
$n\times n$
matrix
![]() $B$
with entries in
$B$
with entries in
![]() $\text{k}^{n}$
none of whose columns are identically
$\text{k}^{n}$
none of whose columns are identically
![]() $0$
. Let
$0$
. Let
![]() $(\vec{v}_{1},\ldots ,\vec{v}_{n})$
be the columns of
$(\vec{v}_{1},\ldots ,\vec{v}_{n})$
be the columns of
![]() $B$
. Let
$B$
. Let
![]() $S_{n}$
be the simplicial complex whose
$S_{n}$
be the simplicial complex whose
![]() $r$
-simplices are chains
$r$
-simplices are chains
The complex
![]() $S_{n}$
is isomorphic to the barycentric subdivision of the boundary of an
$S_{n}$
is isomorphic to the barycentric subdivision of the boundary of an
![]() $(n-1)$
-simplex; in particular,
$(n-1)$
-simplex; in particular,
![]() $S_{n}$
is homeomorphic to an
$S_{n}$
is homeomorphic to an
![]() $(n-2)$
-sphere. There is a simplicial map
$(n-2)$
-sphere. There is a simplicial map
![]() $f:S_{n}\rightarrow {\mathcal{T}}_{\operatorname{GL}_{n}}(\text{k})$
defined via the formula
$f:S_{n}\rightarrow {\mathcal{T}}_{\operatorname{GL}_{n}}(\text{k})$
defined via the formula
The apartment class corresponding to
![]() $B$
, denoted
$B$
, denoted
![]() $\Vert \begin{array}{@{}c@{}}B\end{array}\Vert$
, is the image of the fundamental class
$\Vert \begin{array}{@{}c@{}}B\end{array}\Vert$
, is the image of the fundamental class
![]() $[S_{n}]\in \widetilde{\operatorname{H}}_{n-2}(S_{n};R)=R$
under the map
$[S_{n}]\in \widetilde{\operatorname{H}}_{n-2}(S_{n};R)=R$
under the map
![]() $f_{\ast }:\widetilde{\operatorname{H}}_{n-2}(S_{n};R)\rightarrow \widetilde{\operatorname{H}}_{n-2}({\mathcal{T}}_{\operatorname{GL}_{n}}(\text{k});R)=\operatorname{St}_{\operatorname{GL}_{n}}(\text{k};R)$
.
$f_{\ast }:\widetilde{\operatorname{H}}_{n-2}(S_{n};R)\rightarrow \widetilde{\operatorname{H}}_{n-2}({\mathcal{T}}_{\operatorname{GL}_{n}}(\text{k});R)=\operatorname{St}_{\operatorname{GL}_{n}}(\text{k};R)$
.
Remark 6.5. We have
![]() $\Vert \begin{array}{@{}c@{}}B\end{array}\Vert =0$
if the
$\Vert \begin{array}{@{}c@{}}B\end{array}\Vert =0$
if the
![]() $\vec{v}_{i}$
do not form a basis for
$\vec{v}_{i}$
do not form a basis for
![]() $\text{k}^{n}$
, i.e. if
$\text{k}^{n}$
, i.e. if
![]() $B$
is not invertible.
$B$
is not invertible.
Permuting the columns of
![]() $B$
changes
$B$
changes
![]() $\Vert \begin{array}{@{}c@{}}B\end{array}\Vert$
by the sign of the permutation, and multiplying a column of
$\Vert \begin{array}{@{}c@{}}B\end{array}\Vert$
by the sign of the permutation, and multiplying a column of
![]() $B$
by a nonzero scalar does not change
$B$
by a nonzero scalar does not change
![]() $\Vert \begin{array}{@{}c@{}}B\end{array}\Vert$
. The apartment classes also satisfy the following more interesting relation.
$\Vert \begin{array}{@{}c@{}}B\end{array}\Vert$
. The apartment classes also satisfy the following more interesting relation.
Lemma 6.6. Let
![]() $\text{k}$
be a field, let
$\text{k}$
be a field, let
![]() $R$
be a commutative ring, and let
$R$
be a commutative ring, and let
![]() $n\geqslant 2$
. Let
$n\geqslant 2$
. Let
![]() $B$
be an
$B$
be an
![]() $n\times (n+1)$
-matrix with entries in
$n\times (n+1)$
-matrix with entries in
![]() $\text{k}$
. Assume that none of the columns of
$\text{k}$
. Assume that none of the columns of
![]() $B$
are identically
$B$
are identically
![]() $0$
. Ordering the columns of
$0$
. Ordering the columns of
![]() $B$
from
$B$
from
![]() $0$
to
$0$
to
![]() $n$
, for
$n$
, for
![]() $0\leqslant m\leqslant n$
let
$0\leqslant m\leqslant n$
let
![]() $B_{m}$
be the result of deleting the
$B_{m}$
be the result of deleting the
![]() $m$
th column from
$m$
th column from
![]() $B$
. Then
$B$
. Then
![]() $\Vert \begin{array}{@{}c@{}}B_{0}\end{array}\Vert -\Vert \begin{array}{@{}c@{}}B_{1}\end{array}\Vert +\Vert \begin{array}{@{}c@{}}B_{2}\end{array}\Vert -\cdots +(-1)^{n}\Vert \begin{array}{@{}c@{}}B_{n}\end{array}\Vert =0$
.
$\Vert \begin{array}{@{}c@{}}B_{0}\end{array}\Vert -\Vert \begin{array}{@{}c@{}}B_{1}\end{array}\Vert +\Vert \begin{array}{@{}c@{}}B_{2}\end{array}\Vert -\cdots +(-1)^{n}\Vert \begin{array}{@{}c@{}}B_{n}\end{array}\Vert =0$
.
Proof. The simplices forming the apartment classes
![]() $\Vert \begin{array}{@{}c@{}}B_{i}\end{array}\Vert$
cancel in pairs; see Figure 1.◻
$\Vert \begin{array}{@{}c@{}}B_{i}\end{array}\Vert$
cancel in pairs; see Figure 1.◻
The Solomon–Tits theorem [Reference BrownBro89, Theorem IV.5.2] gives the following basis for
![]() $\operatorname{St}_{\operatorname{GL}_{n}}(\text{k};R)$
.
$\operatorname{St}_{\operatorname{GL}_{n}}(\text{k};R)$
.
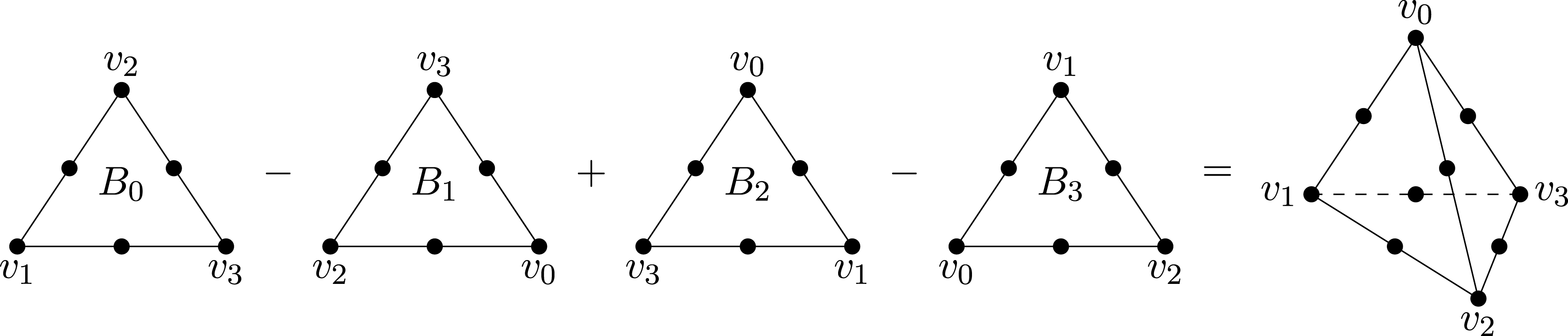
Figure 1. As we illustrate here in the case
![]() $n=3$
, the apartment classes corresponding to the
$n=3$
, the apartment classes corresponding to the
![]() $B_{i}$
can be placed on the boundary of an
$B_{i}$
can be placed on the boundary of an
![]() $n$
-dimensional simplex such that their simplices cancel in pairs. In the picture, the vertices labeled with the vectors
$n$
-dimensional simplex such that their simplices cancel in pairs. In the picture, the vertices labeled with the vectors
![]() $\vec{v}_{i}$
are taken to the lines spanned by the
$\vec{v}_{i}$
are taken to the lines spanned by the
![]() $\vec{v}_{i}$
while the unlabeled vertices are taken to the two-dimensional subspaces spanned by the vectors on their two neighbors.
$\vec{v}_{i}$
while the unlabeled vertices are taken to the two-dimensional subspaces spanned by the vectors on their two neighbors.
Theorem 6.7 (Solomon–Tits).
Let
![]() $\text{k}$
be a field, let
$\text{k}$
be a field, let
![]() $R$
be a commutative ring, and let
$R$
be a commutative ring, and let
![]() $n\geqslant 1$
. Then
$n\geqslant 1$
. Then
![]() $\operatorname{St}_{\operatorname{GL}_{n}}(\text{k};R)$
is a free
$\operatorname{St}_{\operatorname{GL}_{n}}(\text{k};R)$
is a free
![]() $R$
-module on the basis consisting of all
$R$
-module on the basis consisting of all
![]() $\Vert \begin{array}{@{}c@{}}B\end{array}\Vert$
such that
$\Vert \begin{array}{@{}c@{}}B\end{array}\Vert$
such that
![]() $B$
is an upper unitriangular matrix in
$B$
is an upper unitriangular matrix in
![]() $\operatorname{GL}_{n}(\text{k})$
.
$\operatorname{GL}_{n}(\text{k})$
.
6.5 The proof of Lemma 6.4
We finally prove Lemma 6.4, which as discussed in § 6.3 suffices to prove Lemma 6.1. First, we recall its statement. For
![]() $1\leqslant m\leqslant 3$
, let
$1\leqslant m\leqslant 3$
, let
![]() $\unicode[STIX]{x1D701}_{m}$
and
$\unicode[STIX]{x1D701}_{m}$
and
![]() $\widehat{\unicode[STIX]{x1D705}}_{m}$
be as in § 6.2. Define
$\widehat{\unicode[STIX]{x1D705}}_{m}$
be as in § 6.2. Define
via the formula
![]() $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D701}_{1}-\unicode[STIX]{x1D701}_{2}+\unicode[STIX]{x1D701}_{3}$
. Our goal is to prove that
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D701}_{1}-\unicode[STIX]{x1D701}_{2}+\unicode[STIX]{x1D701}_{3}$
. Our goal is to prove that
![]() $\unicode[STIX]{x1D701}$
is surjective.
$\unicode[STIX]{x1D701}$
is surjective.
Before we do that, we introduce some formulas. Let
![]() $\unicode[STIX]{x1D70B}:\operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)\rightarrow \operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)$
be the composition
$\unicode[STIX]{x1D70B}:\operatorname{St}_{\operatorname{GL}_{3}}(\text{k};R)\rightarrow \operatorname{St}_{\operatorname{GL}_{2}}(\text{k};R)$
be the composition
where the first arrow is the Reeder projection map and the second arrow comes from the fact that
![]() $\operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)=R$
. From its definition, we see that
$\operatorname{St}_{\operatorname{GL}_{1}}(\text{k};R)=R$
. From its definition, we see that
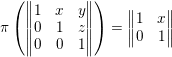 $$\begin{eqnarray}\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & x & y\\ 0 & 1 & z\\ 0 & 0 & 1\end{array}\right\Vert \right)=\left\Vert \begin{array}{@{}cc@{}}1 & x\\ 0 & 1\end{array}\right\Vert\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & x & y\\ 0 & 1 & z\\ 0 & 0 & 1\end{array}\right\Vert \right)=\left\Vert \begin{array}{@{}cc@{}}1 & x\\ 0 & 1\end{array}\right\Vert\end{eqnarray}$$
for all
![]() $x,y,z\in \text{k}$
. What is more, for all
$x,y,z\in \text{k}$
. What is more, for all
![]() $3\times 3$
matrices
$3\times 3$
matrices
![]() $B$
none of whose columns are identically
$B$
none of whose columns are identically
![]() $0$
we have
$0$
we have
Here the
![]() $\widehat{\unicode[STIX]{x1D705}}_{m}$
act on
$\widehat{\unicode[STIX]{x1D705}}_{m}$
act on
![]() $B$
via matrix multiplication.
$B$
via matrix multiplication.
We now turn to proving that
![]() $\unicode[STIX]{x1D701}$
is surjective. Consider
$\unicode[STIX]{x1D701}$
is surjective. Consider
![]() $a\in \text{k}$
, and set
$a\in \text{k}$
, and set
By Theorem 6.7, it is enough to prove that
![]() $A_{a}\in \operatorname{Im}(\unicode[STIX]{x1D701})$
. We have
$A_{a}\in \operatorname{Im}(\unicode[STIX]{x1D701})$
. We have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & a & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert \right) & = & \displaystyle \unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}0 & 0 & -1\\ 0 & 1 & 0\\ 1 & a & 0\end{array}\right\Vert \right)-\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & a & 0\\ 0 & 0 & -1\\ 0 & 1 & 0\end{array}\right\Vert \right)+\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & a & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert \right)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}\left(-\left\Vert \begin{array}{@{}ccc@{}}-1 & 0 & 0\\ 0 & 1 & 0\\ 0 & a & 1\end{array}\right\Vert \right)-\unicode[STIX]{x1D70B}\left(-\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & a\\ 0 & -1 & 0\\ 0 & 0 & 1\end{array}\right\Vert \right)+\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & a & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert \right)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}\left(-\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & a & 1\end{array}\right\Vert \right)-\unicode[STIX]{x1D70B}\left(-\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & a\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert \right)+\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & a & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert \right)\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & a & 1\end{array}\right\Vert \right)+\left\Vert \begin{array}{@{}cc@{}}1 & 0\\ 0 & 1\end{array}\right\Vert +\left\Vert \begin{array}{@{}cc@{}}1 & a\\ 0 & 1\end{array}\right\Vert ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & a & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert \right) & = & \displaystyle \unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}0 & 0 & -1\\ 0 & 1 & 0\\ 1 & a & 0\end{array}\right\Vert \right)-\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & a & 0\\ 0 & 0 & -1\\ 0 & 1 & 0\end{array}\right\Vert \right)+\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & a & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert \right)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}\left(-\left\Vert \begin{array}{@{}ccc@{}}-1 & 0 & 0\\ 0 & 1 & 0\\ 0 & a & 1\end{array}\right\Vert \right)-\unicode[STIX]{x1D70B}\left(-\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & a\\ 0 & -1 & 0\\ 0 & 0 & 1\end{array}\right\Vert \right)+\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & a & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert \right)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}\left(-\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & a & 1\end{array}\right\Vert \right)-\unicode[STIX]{x1D70B}\left(-\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & a\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert \right)+\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & a & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert \right)\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & a & 1\end{array}\right\Vert \right)+\left\Vert \begin{array}{@{}cc@{}}1 & 0\\ 0 & 1\end{array}\right\Vert +\left\Vert \begin{array}{@{}cc@{}}1 & a\\ 0 & 1\end{array}\right\Vert ,\end{eqnarray}$$
where the second equality uses the fact that permuting the columns of a matrix changes the associated apartment by the sign of the permutation and the third equality uses the fact that multiplying a column by a nonzero scalar does not change the associated apartment.
If
![]() $a=0$
, then the right-hand side of (6.4) simplifies to
$a=0$
, then the right-hand side of (6.4) simplifies to
so
![]() $A_{0}\in \operatorname{Im}(\unicode[STIX]{x1D701})$
. Assume now that
$A_{0}\in \operatorname{Im}(\unicode[STIX]{x1D701})$
. Assume now that
![]() $a\neq 0$
. Plugging the matrix
$a\neq 0$
. Plugging the matrix
 $$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}1 & 0 & 0 & 0\\ 0 & 1 & 1 & 0\\ 0 & 0 & a & 1\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}1 & 0 & 0 & 0\\ 0 & 1 & 1 & 0\\ 0 & 0 & a & 1\end{array}\right)\end{eqnarray}$$
into Lemma 6.6, we get the relation
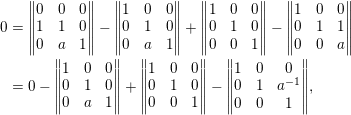 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \left\Vert \begin{array}{@{}ccc@{}}0 & 0 & 0\\ 1 & 1 & 0\\ 0 & a & 1\end{array}\right\Vert -\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & a & 1\end{array}\right\Vert +\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert -\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 1\\ 0 & 0 & a\end{array}\right\Vert \nonumber\\ \displaystyle & = & \displaystyle 0-\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & a & 1\end{array}\right\Vert +\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert -\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & a^{-1}\\ 0 & 0 & 1\end{array}\right\Vert ,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \left\Vert \begin{array}{@{}ccc@{}}0 & 0 & 0\\ 1 & 1 & 0\\ 0 & a & 1\end{array}\right\Vert -\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & a & 1\end{array}\right\Vert +\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert -\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 1\\ 0 & 0 & a\end{array}\right\Vert \nonumber\\ \displaystyle & = & \displaystyle 0-\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & a & 1\end{array}\right\Vert +\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert -\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & a^{-1}\\ 0 & 0 & 1\end{array}\right\Vert ,\nonumber\end{eqnarray}$$
where the equality uses the fact that the columns of the first matrix are not linearly independent and the fact that multiplying a column of a matrix by a nonzero scalar does not change the associated apartment. Plugging this relation into (6.4), we see that the right-hand side of (6.4) equals
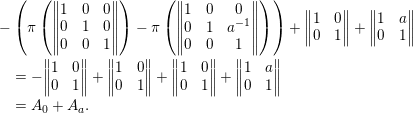 $$\begin{eqnarray}\displaystyle & & \displaystyle -\left(\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert \right)-\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & a^{-1}\\ 0 & 0 & 1\end{array}\right\Vert \right)\right)+\left\Vert \begin{array}{@{}cc@{}}1 & 0\\ 0 & 1\end{array}\right\Vert +\left\Vert \begin{array}{@{}cc@{}}1 & a\\ 0 & 1\end{array}\right\Vert \nonumber\\ \displaystyle & & \displaystyle \quad =-\left\Vert \begin{array}{@{}cc@{}}1 & 0\\ 0 & 1\end{array}\right\Vert +\left\Vert \begin{array}{@{}cc@{}}1 & 0\\ 0 & 1\end{array}\right\Vert +\left\Vert \begin{array}{@{}cc@{}}1 & 0\\ 0 & 1\end{array}\right\Vert +\left\Vert \begin{array}{@{}cc@{}}1 & a\\ 0 & 1\end{array}\right\Vert \nonumber\\ \displaystyle & & \displaystyle \quad =A_{0}+A_{a}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\left(\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right\Vert \right)-\unicode[STIX]{x1D70B}\left(\left\Vert \begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & a^{-1}\\ 0 & 0 & 1\end{array}\right\Vert \right)\right)+\left\Vert \begin{array}{@{}cc@{}}1 & 0\\ 0 & 1\end{array}\right\Vert +\left\Vert \begin{array}{@{}cc@{}}1 & a\\ 0 & 1\end{array}\right\Vert \nonumber\\ \displaystyle & & \displaystyle \quad =-\left\Vert \begin{array}{@{}cc@{}}1 & 0\\ 0 & 1\end{array}\right\Vert +\left\Vert \begin{array}{@{}cc@{}}1 & 0\\ 0 & 1\end{array}\right\Vert +\left\Vert \begin{array}{@{}cc@{}}1 & 0\\ 0 & 1\end{array}\right\Vert +\left\Vert \begin{array}{@{}cc@{}}1 & a\\ 0 & 1\end{array}\right\Vert \nonumber\\ \displaystyle & & \displaystyle \quad =A_{0}+A_{a}.\nonumber\end{eqnarray}$$
Since we have already seen that
![]() $A_{0}\in \operatorname{Im}(\unicode[STIX]{x1D701})$
, we deduce that
$A_{0}\in \operatorname{Im}(\unicode[STIX]{x1D701})$
, we deduce that
![]() $A_{a}\in \operatorname{Im}(\unicode[STIX]{x1D701})$
, as desired.
$A_{a}\in \operatorname{Im}(\unicode[STIX]{x1D701})$
, as desired.