Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-28T12:27:25.090Z Has data issue: false hasContentIssue false
  • English
  • Français

The Grothendieck–Serre conjecture over valuation rings

Part of: Special varieties (Co)homology theory Local theory Algebraic groups

Published online by Cambridge University Press:  05 January 2024

Ning Guo Open the ORCID record for Ning Guo [Opens in a new window]
Ning Guo*
Affiliation:
St. Petersburg branch of V. A. Steklov Mathematical Institute, Fontanka 27, 191023 St. Petersburg, Russia guo.ning@eimi.ru Département de Mathématiques, Université Paris-Saclay, Orsay Cedex, France
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we establish the Grothendieck–Serre conjecture over valuation rings: for a reductive group scheme 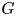$G$ over a valuation ring 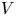$V$ with fraction field 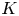$K$, a 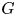$G$-torsor over 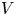$V$ is trivial if it is trivial over 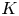$K$. This result is predicted by the original Grothendieck–Serre conjecture and the resolution of singularities. The novelty of our proof lies in overcoming subtleties brought by general nondiscrete valuation rings. By using flasque resolutions and inducting with local cohomology, we prove a non-Noetherian counterpart of Colliot-Thélène–Sansuc's case of tori. Then, taking advantage of techniques in algebraization, we obtain the passage to the Henselian rank-one case. Finally, we induct on Levi subgroups and use the integrality of rational points of anisotropic groups to reduce to the semisimple anisotropic case, in which we appeal to properties of parahoric subgroups in Bruhat–Tits theory to conclude. In the last section, by using extension properties of reflexive sheaves on formal power series over valuation rings and patching of torsors, we prove a variant of Nisnevich's purity conjecture.

Keywords

torsorétale cohomologyGrothendieck–Serre conjectureprincipal bundlehomogeneous spacegroup schemevaluation ring

MSC classification

Primary: 14L15: Group schemes
Secondary: 14B15: Local cohomology 14M17: Homogeneous spaces and generalizations 14L30: Group actions on varieties or schemes (quotients) 14F17: Vanishing theorems
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 2 , February 2024 , pp. 317 - 355
Check for updates
Copyright
© 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abhyankar, S., Local uniformization on algebraic surfaces over ground fields of characteristic $p\ne 0$, Ann. of Math. (2) 63 (1956), 491–526.CrossRefGoogle Scholar
Abhyankar, S. S., Resolution of singularities of embedded algebraic surfaces, Pure and Applied Mathematics, vol. 24 (Academic Press, New York–London, 1966).Google Scholar
Alper, J., Adequate moduli spaces and geometrically reductive group schemes, Algebr. Geom. 1 (2014), 489–531.CrossRefGoogle Scholar
Barnes, D. W., On Cartan subalgebras of Lie algebras, Math. Z. 101 (1967), 350–355.CrossRefGoogle Scholar
Bhatt, B. and Mathew, A., The $\operatorname {arc}$-topology, Duke Math. J. 170 (2021), 1899–1988.CrossRefGoogle Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 21 (Springer, Berlin, 1990).CrossRefGoogle Scholar
Bourbaki, N., Commutative algebra, in Elements of mathematics (Springer, Berlin, 1998), chs 1–7, translated from the French, reprint of the 1989 English translation.Google Scholar
Bouthier, A. and Česnavičius, K., Torsors on loop groups and the Hitchin fibration, Ann. Sci. Éc. Norm. Supér. 55 (2022), 791–864.CrossRefGoogle Scholar
Bruhat, F. and Tits, J., Groupes réductifs sur un corps local. II. Schémas en groupes. Existence d'une donnée radicielle valuée, Inst. Hautes Études Sci. Publ. Math. 60 (1984), 197–376.Google Scholar
Česnavičius, K., Topology on cohomology of local fields, Forum Math. Sigma 3 (2015), e16, 55, MR3482265.CrossRefGoogle Scholar
Česnavičius, K., Grothendieck–Serre in the quasi-split unramified case, Forum Math. Pi 10 (2022), 30.CrossRefGoogle Scholar
Česnavičius, K., Problems about torsors over regular rings, Acta Math. Vietnam. 47 (2022), 39–107.CrossRefGoogle Scholar
Choi, M. D., Lam, T. Y., Reznick, B. and Rosenberg, A., Sums of squares in some integral domains, J. Algebra 65 (1980), 234–256.CrossRefGoogle Scholar
Colliot-Thélène, J.-L. and Sansuc, J.-J., Cohomologie des groupes de type multiplicatif sur les schémas réguliers, C. R. Acad. Sci. Paris Sér. A-B 287 (1978), A449–A452.Google Scholar
Colliot-Thélène, J.-L. and Sansuc, J.-J., Principal homogeneous spaces under flasque tori: applications, J. Algebra 106 (1987), 148–205; MR878473.CrossRefGoogle Scholar
Conrad, B., Weil and Grothendieck approaches to adelic points, Enseign. Math. (2) 58 (2012), 61–97.CrossRefGoogle Scholar
Conrad, B., Reductive group schemes, in Autour des schémas en groupes: École d'été “Schémas en groupes”, Group Schemes, A celebration of SGA3, vol. I (Société Mathématique de France, Paris, 2014), 93–444.Google Scholar
Cossart, V. and Piltant, O., Resolution of singularities of threefolds in positive characteristic. I. Reduction to local uniformization on Artin-Schreier and purely inseparable coverings, J. Algebra 320 (2008), 1051–1082.CrossRefGoogle Scholar
Cossart, V. and Piltant, O., Resolution of singularities of threefolds in positive characteristic. II, J. Algebra 321 (2009), 1836–1976.CrossRefGoogle Scholar
Cutkosky, S. D., Resolution of singularities for 3-folds in positive characteristic, Amer. J. Math. 131 (2009), 59–127.CrossRefGoogle Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique. I. Le langage des schémas, Inst. Hautes Études Sci. Publ. Math. 4 (1960), 228; MR0217083 (36 #177a).CrossRefGoogle Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. II, Inst. Hautes Études Sci. Publ. Math. 24 (1965), 231; MR0199181 (33 #7330) (French).Google Scholar
Grothendieck, A. and Dieudonné, J. A. E., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV, Inst. Hautes Études Sci. Publ. Math. 32 (1967), 361; MR0238860 (39 #220) (French).Google Scholar
Engler, A. J. and Prestel, A., Valued fields, Springer Monographs in Mathematics (Springer, Berlin, 2005).Google Scholar
Fedorov, R., On the purity conjecture of Nisnevich for torsors under reductive group schemes, Preprint (2021), arXiv:2109.10332.Google Scholar
Fedorov, R., On the Grothendieck-Serre conjecture on principal bundles in mixed characteristic, Trans. Amer. Math. Soc. 375 (2022), 559–586.CrossRefGoogle Scholar
Fedorov, R. and Panin, I., A proof of the Grothendieck–Serre conjecture on principal bundles over regular local rings containing infinite fields, Publ. Math. Inst. Hautes Études Sci. 122 (2015), 169–193; MR3415067.CrossRefGoogle Scholar
Florence, M. and Gille, P., Residues on affine Grassmannians, J. Reine Angew. Math. 776 (2021), 119–150.CrossRefGoogle Scholar
Fujiwara, K. and Kato, F., Foundations of rigid geometry. I, EMS Monographs in Mathematics (European Mathematical Society (EMS), Zürich, 2018).CrossRefGoogle Scholar
Gabber, O., Some theorems in Azumaya algebras, in Groupe de Brauer, Lecture Notes in Mathematics, vol. 844 (Springer, 1981), 129–209.CrossRefGoogle Scholar
Gabber, O., Gille, P. and Moret-Bailly, L., Fibrés principaux sur les corps valués henséliens, Algebr. Geom. 1 (2014), 573–612; MR3296806.CrossRefGoogle Scholar
Gabber, O. and Ramero, L., Foundations for almost ring theory, Preprint (2018), arXiv:math/0409584.Google Scholar
Giraud, J., Cohomologie non abélienne, Grundlehren der mathematischen Wissenschaften, vol. 179 (Springer, Cham, 1971).CrossRefGoogle Scholar
Grothendieck, A., Torsion homologique et sections rationnelles, in Anneaux de Chow et applications, Séminaire Claude Chevalley (2e année), vol. 3 (Secrétariat Mathématique, École Normale Supérieure, Paris, 1958), Exp. no. 5, 1–29.Google Scholar
Grothendieck, A., Le groupe de Brauer. II. Théorie cohomologique, in Dix exposés sur la cohomologie des schémas (North-Holland, Amsterdam; Masson, Paris, 1968), 67–87.Google Scholar
Guo, N. and Liu, F., Grothendieck–Serre for constant reductive group schemes, Preprint (2023), arXiv:2301.12460.Google Scholar
Guo, N. and Panin, I., On the Grothendieck–Serre conjecture for projective smooth schemes over a DVR, Preprint (2023), arXiv:2302.02842.Google Scholar
Harder, G., Eine Bemerkung zum schwachen Approximationssatz, Arch. Math. (Basel) 19 (1968), 465–471.CrossRefGoogle Scholar
Huber, R., Étale cohomology of rigid analytic varieties and adic spaces, Aspects of Mathematics, E30 (Friedrich Vieweg & Sohn, Braunschweig, 1996).CrossRefGoogle Scholar
Maculan, M., Maximality of hyperspecial compact subgroups avoiding Bruhat–Tits theory, Ann. Inst. Fourier (Grenoble) 67 (2017), 1–21.CrossRefGoogle Scholar
Milne, J. S., Étale cohomology, Princeton Mathematical Series, vol. 33 (Princeton University Press, Princeton, NJ, 1980).Google Scholar
Moret-Bailly, L., Problèmes de Skolem sur les champs algébriques, Compos. Math. 125 (2001), 1–30.CrossRefGoogle Scholar
Nagata, M., Finitely generated rings over a valuation ring, J. Math. Kyoto Univ. 5 (1966), 163–169.Google Scholar
Nisnevich, Y. A., Rationally trivial principal homogeneous spaces, purity and arithmetic of reductive group schemes over extensions of two-dimensional regular local rings, C. R. Acad. Sci. Paris Sér. I Math. 309 (1989), 651–655; MR1054270.Google Scholar
Panin, I., Proof of the Grothendieck–Serre conjecture on principal bundles over regular local rings containing a field, Izv. Ross. Akad. Nauk Ser. Mat. 84 (2020), 169–186.Google Scholar
Panin, I. and Stavrova, A., On the Gille theorem for the relative projective line: I, Preprint (2023), arXiv:2304.09465.Google Scholar
Panin, I. and Stavrova, A., On the Gille theorem for the relative projective line: II, Preprint (2023), arXiv:2305.16627.Google Scholar
Perez-Garcia, C. and Schikhof, W. H., Locally convex spaces over non-Archimedean valued fields, Cambridge Studies in Advanced Mathematics, vol. 119 (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Prasad, G., Elementary proof of a theorem of Bruhat-Tits-Rousseau and of a theorem of Tits, Bull. Soc. Math. France 110 (1982), 197–202.CrossRefGoogle Scholar
Quillen, D., Projective modules over polynomial rings, Invent. Math. 36 (1976), 167–171.CrossRefGoogle Scholar
Rousseau, G., Immeubles des groupes réducitifs sur les corps locaux (U.E.R. Mathématique, Université Paris XI, Orsay, 1977). Thèse de doctorat, Publications Mathématiques d'Orsay, No. 221-77.68.Google Scholar
Scholze, P., Perfectoid spaces, Publ. Math. Inst. Hautes Études Sci. 116 (2012), 245–313.CrossRefGoogle Scholar
Serre, J.-P., Espaces fibrés algébriques, in Anneaux de Chow et applications, Séminaire Claude Chevalley (2e année), vol.~3 (Secrétariat Mathématique, École Normale Supérieure, Paris, 1958), Exp. no. 1, 1–37.Google Scholar
Serre, J.-P., Galois cohomology, Springer Monographs in Mathematics (Springer, 2002); MR1867431 (2002i:12004).Google Scholar
Revêtements étales et groupe fondamental (SGA 1), Documents Mathématiques (Paris) [Mathematical Documents (Paris)], 3, Séminaire de géométrie algébrique du Bois Marie 1960–61. [Algebraic Geometry Seminar of Bois Marie 1960–61]; Directed by A. Grothendieck; With two papers by M. Raynaud; Updated and annotated reprint of the 1971 original [Lecture Notes in Mathematics, 224, Springer, Berlin; MR0354651 (50 #7129)] (Société Mathématique de France, Paris, 2003); MR2017446 (2004g:14017).Google Scholar
Schémas en groupes. II: Groupes de type multiplicatif, et structure des schémas en groupes généraux. Séminaire de Géométrie Algébrique du Bois Marie 1962/64 (SGA 3). Dirigé par M. Demazure et A. Grothendieck. Lecture Notes in Mathematics, vol. 152 (Springer, Berlin-New York, 1970); MR0274459 (43 #223b).Google Scholar
Gille, P. and Polo, P. (eds.), Schémas en groupes (SGA 3). Tome III. Structure des schémas en groupes réductifs. Documents Mathématiques (Paris) [Mathematical Documents (Paris)], 8, Séminaire de Géométrie Algébrique du Bois Marie 1962–64. [Algebraic Geometry Seminar of Bois Marie 1962–64]; A seminar directed by M. Demazure and A. Grothendieck with the collaboration of M. Artin, J.-E. Bertin, P. Gabriel, M. Raynaud and J-P. Serre; Revised and annotated edition of the 1970 French original; MR2867622.Google Scholar
Théorie des topos et cohomologie étale des schémas. Tome 2, Lecture Notes in Mathematics, vol. 270, Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4); Dirigé par M. Artin, A. Grothendieck et J. L. Verdier. Avec la collaboration de N. Bourbaki, P. Deligne et B. Saint-Donat; MR0354653 (50 #7131).Google Scholar
The Stacks Project Authors, Stacks Project (2018), https://stacks.math.columbia.edu.Google Scholar
Temkin, M., Inseparable local uniformization, J. Algebra 373 (2013), 65–119.CrossRefGoogle Scholar
Temkin, M., Tame distillation and desingularization by $p$-alterations, Ann. of Math. (2) 186 (2017), 97–126.CrossRefGoogle Scholar
Zariski, O., Local uniformization on algebraic varieties, Ann. of Math. (2) 41 (1940), 852–896.CrossRefGoogle Scholar