Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-27T09:02:46.125Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics on ℙ1: preperiodic points and pairwise stability

Part of: Arithmetic and non-Archimedean dynamical systems Arithmetic algebraic geometry Complex dynamical systems

Published online by Cambridge University Press:  05 January 2024

Laura DeMarco  and
Niki Myrto Mavraki
Laura DeMarco
Affiliation:
Department of Mathematics, Harvard University, Science Center Room 325, 1 Oxford Street, Cambridge, MA 02138, USA demarco@math.harvard.edu
Niki Myrto Mavraki
Affiliation:
Department of Mathematics, University of Toronto, Bahen Centre, 40 St. George Street, Toronto, Ontario, M5S 2E4, Canada myrto.mavraki@utoronto.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

DeMarco, Krieger, and Ye conjectured that there is a uniform bound B, depending only on the degree d, so that any pair of holomorphic maps 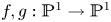$f, g :{\mathbb {P}}^1\to {\mathbb {P}}^1$ with degree 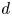$d$ will either share all of their preperiodic points or have at most 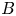$B$ in common. Here we show that this uniform bound holds for a Zariski open and dense set in the space of all pairs, 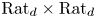$\mathrm {Rat}_d \times \mathrm {Rat}_d$, for each degree $d\geq 2$. The proof involves a combination of arithmetic intersection theory and complex-dynamical results, especially as developed recently by Gauthier and Vigny, Yuan and Zhang, and Mavraki and Schmidt. In addition, we present alternate proofs of the main results of DeMarco, Krieger, and Ye [Uniform Manin-Mumford for a family of genus 2 curves, Ann. of Math. (2) 191 (2020), 949–1001; Common preperiodic points for quadratic polynomials, J. Mod. Dyn. 18 (2022), 363–413] and of Poineau [Dynamique analytique sur 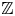$\mathbb {Z}$ II : Écart uniforme entre Lattès et conjecture de Bogomolov-Fu-Tschinkel, Preprint (2022), arXiv:2207.01574 [math.NT]]. In fact, we prove a generalization of a conjecture of Bogomolov, Fu, and Tschinkel in a mixed setting of dynamical systems and elliptic curves.

Keywords

equidistributionheightscurrentsbifurcationrational functionspreperiodic points

MSC classification

Primary: 37F10: Polynomials; rational maps; entire and meromorphic functions 37P15: Global ground fields
Secondary: 11G50: Heights
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 2 , February 2024 , pp. 356 - 387
Check for updates
Copyright
© 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, I. N. and Erëmenko, A., A problem on Julia sets, Ann. Acad. Sci. Fenn. Ser. A I Math. 12 (1987), 229–236.CrossRefGoogle Scholar
Baker, M. and DeMarco, L., Preperiodic points and unlikely intersections, Duke Math. J. 159 (2011), 1–29.CrossRefGoogle Scholar
Bassanelli, G. and Berteloot, F., Bifurcation currents in holomorphic dynamics on $\Bbb P^k$, J. Reine Angew. Math. 608 (2007), 201–235.Google Scholar
Berteloot, F., Bianchi, F. and Dupont, C., Dynamical stability and Lyapunov exponents for holomorphic endomorphisms of $\Bbb P^k$, Ann. Sci. Éc. Norm. Supér. (4) 51 (2018), 215–262.CrossRefGoogle Scholar
Bogomolov, F., Fu, H. and Tschinkel, Y., Torsion of elliptic curves and unlikely intersections, in Geometry and physics, vol. I (Oxford University Press, Oxford, 2018), 19–37.Google Scholar
Buff, X. and Epstein, A., Bifurcation measure and postcritically finite rational maps, in Complex dynamics (A K Peters, Wellesley, MA, 2009), 491–512.CrossRefGoogle Scholar
Call, G. S. and Silverman, J. H., Canonical heights on varieties with morphisms, Compos. Math. 89 (1993), 163–205.Google Scholar
DeMarco, L., Dynamics of rational maps: a current on the bifurcation locus, Math. Res. Lett. 8 (2001), 57–66.CrossRefGoogle Scholar
DeMarco, L., Dynamics of rational maps: Lyapunov exponents, bifurcations, and capacity, Math. Ann. 326 (2003), 43–73.CrossRefGoogle Scholar
DeMarco, L., Iteration at the boundary of the space of rational maps, Duke Math. J. 130 (2005), 169–197.CrossRefGoogle Scholar
DeMarco, L., Bifurcations, intersections, and heights, Algebra Number Theory 10 (2016), 1031–1056.CrossRefGoogle Scholar
DeMarco, L., Krieger, H. and Ye, H., Uniform Manin-Mumford for a family of genus 2 curves, Ann. of Math. (2) 191 (2020), 949–1001.CrossRefGoogle Scholar
DeMarco, L., Krieger, H. and Ye, H., Common preperiodic points for quadratic polynomials, J. Mod. Dyn. 18 (2022), 363–413.CrossRefGoogle Scholar
Dimitrov, V., Gao, Z. and Habegger, P., Uniform bound for the number of rational points on a pencil of curves, Int. Math. Res. Not. IMRN 2021 (2021), 1138–1159.CrossRefGoogle Scholar
Dimitrov, V., Gao, Z. and Habegger, P., Uniformity in Mordell-Lang for curves, Ann. of Math. (2) 194 (2021), 237–298.CrossRefGoogle Scholar
Doyle, J. and Hyde, T., Polynomials with many rational preperiodic points, Preprint (2022), arXiv:2201.11707 [math.DS].Google Scholar
Dujardin, R. and Favre, C., Distribution of rational maps with a preperiodic critical point, Amer. J. Math. 130 (2008), 979–1032.CrossRefGoogle Scholar
Freire, A., Lopes, A. and Mañé, R., An invariant measure for rational maps, Bol. Soc. Braz. Mat. 14 (1983), 45–62.CrossRefGoogle Scholar
Gao, Z., Generic rank of Betti map and unlikely intersections, Compos. Math. 156 (2020), 2469–2509.CrossRefGoogle Scholar
Gao, Z., Mixed Ax-Schanuel for the universal abelian varieties and some applications, Compos. Math. 156 (2020), 2263–2297.CrossRefGoogle Scholar
Gao, Z., Recent developments of the uniform Mordell-Lang conjecture, Preprint (2021), arXiv:2104.03431v5 [math.NT].Google Scholar
Gao, Z., Ge, T. and Kühne, L., The uniform Mordell-Lang conjecture, Preprint (2021), arXiv:2105.15085v2 [math.NT].Google Scholar
Gao, Z. and Habegger, P., Heights in families of abelian varieties and the geometric Bogomolov conjecture, Ann. of Math. (2) 189 (2019), 527–604.CrossRefGoogle Scholar
Gauthier, T., Good height functions on quasiprojective varieties: equidistribution and applications in dynamics, Preprint (2021), arXiv:2105.02479v3 [math.NT].Google Scholar
Gauthier, T., Taflin, J. and Vigny, G., Sparsity of postcritically finite maps of $\mathbb {P}^k$ and beyond: a complex analytic approach, Preprint (2023), arXiv:2305.02246 [math.DS].Google Scholar
Gauthier, T. and Vigny, G., The geometric dynamical Northcott and Bogomolov properties, Preprint (2019), arXiv:1912.07907v2 [math.DS].Google Scholar
Habegger, P., Special points on fibered powers of elliptic surfaces, J. Reine Angew. Math. 685 (2013), 143–179.Google Scholar
Klimek, M., Pluripotential theory, Oxford Science Publications (Clarendon Press, New York, 1991).CrossRefGoogle Scholar
Kühne, L., Equidistribution in families of abelian varieties and uniformity, Preprint (2021), arXiv:2101.10272v3 [math.NT].Google Scholar
Kühne, L., The relative Bogomolov conjecture for fibered products of elliptic surfaces, J. Reine Angew. Math. 795 (2023), 243–270.Google Scholar
Levin, G. and Przytycki, F., When do two rational functions have the same Julia set? Proc. Amer. Math. Soc. 125 (1997), 2179–2190.CrossRefGoogle Scholar
Lyubich, M., Entropy properties of rational endomorphisms of the Riemann sphere, Ergodic Theory Dynam. Systems 3 (1983), 351–385.CrossRefGoogle Scholar
Lyubich, M. Y., Some typical properties of the dynamics of rational mappings, Uspekhi Mat. Nauk 38 (1983), 197–198.Google Scholar
Mañé, R., On the uniqueness of the maximizing measure for rational maps, Bol. Soc. Braz. Mat. 14 (1983), 27–43.CrossRefGoogle Scholar
Mañé, R., Sad, P. and Sullivan, D., On the dynamics of rational maps, Ann. Sci. Éc. Norm. Supér. 16 (1983), 193–217.CrossRefGoogle Scholar
Mavraki, N. M. and Schmidt, H., On the dynamical Bogomolov conjecture for families of split rational maps, Preprint (2022), arXiv:2201.10455v3 [math.NT].Google Scholar
McMullen, C. T., Families of rational maps and iterative root-finding algorithms, Ann. of Math. (2) 125 (1987), 467–493.CrossRefGoogle Scholar
McMullen, C. T., Complex dynamics and renormalization (Princeton University Press, Princeton, NJ, 1994).Google Scholar
Milnor, J., On Lattès maps, in Dynamics on the Riemann sphere (European Mathematical Society, Zürich, 2006), 9–43.CrossRefGoogle Scholar
Pakovich, F., On iterates of rational functions with maximal number of critical values, Preprint (2021), arXiv:2107.05963v1 [math.DS].Google Scholar
Poineau, J., Dynamique analytique sur $\mathbb {Z}$ II: Écart uniforme entre Lattès et conjecture de Bogomolov-Fu-Tschinkel, Preprint (2022), arXiv:2207.01574 [math.NT].Google Scholar
Ye, H., Rational functions with identical measure of maximal entropy, Adv. Math. 268 (2015), 373–395.CrossRefGoogle Scholar
Yuan, X., Arithmetic bigness and a uniform Bogomolov-type result, Preprint (2021), arXiv:2108.05625v2 [math.NT].Google Scholar
Yuan, X. and Zhang, S., The arithmetic Hodge index theorem for adelic line bundles II, Preprint (2013), arXiv:1304.3539v2 [math.NT].Google Scholar
Yuan, X. and Zhang, S., Adelic line bundles over quasiprojective varieties, Preprint (2021), arXiv:2105.13587v4 [math.NT].Google Scholar
Zdunik, A., Parabolic orbifolds and the dimension of the maximal measure for rational maps, Invent. Math. 99 (1990), 627–649.CrossRefGoogle Scholar