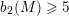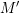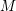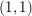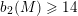1 Introduction
Since the early 2000s, K3 surfaces have been one of the prime subjects of holomorphic dynamics [Reference CantatCan01, Reference McMullenMcM02]. By now, the dynamics of automorphism groups acting on K3 surfaces is rather well understood [Reference Cantat and DupontCD14]. Some of these results are already generalized to irreducible holomorphic symplectic manifolds of Kähler type (simple hyperkähler manifolds) in any dimension [Reference OguisoOgu14].
The purpose of the present paper is to construct sufficiently many interesting automorphisms on a deformation of an arbitrary hyperkähler manifold (see § 2 for basic definitions and properties of hyperkähler manifolds).
For known examples of hyperkähler manifolds, associated with a K3 surface or an abelian surface, it is not hard to find a deformation which admits a large automorphism group. Indeed, we can lift an automorphism of a K3 surface or a torus, or use some other explicit construction (see e.g. [Reference Hassett and TschinkelHT15] and references therein for some examples of automorphisms which do not come from the surface). However, the classification problem for hyperkähler manifolds still looks out of reach, and finding deformations with interesting automorphism groups without referring to the explicit geometry is much less obvious.
An even more complicated problem is to find
![]() $n$
to 1 rational correspondences (‘rational isogenies’) from a manifold to itself or to some other hyperkähler manifold. Such constructions are of considerable importance, but the visible ways to approach this problem look rather difficult at the moment.
$n$
to 1 rational correspondences (‘rational isogenies’) from a manifold to itself or to some other hyperkähler manifold. Such constructions are of considerable importance, but the visible ways to approach this problem look rather difficult at the moment.
What makes possible the study of automorphisms, rather than isogenies, is that the group of automorphisms of a hyperkähler manifold can be understood in terms of its period lattice (that is, the Hodge structure on the second cohomology and the Bogomolov–Beauville–Fujiki (BBF) form, see § 2.1) and the Kähler cone. The latter is described in terms of certain cohomology classes called MBM (monodromy birationally minimal) classes (Definitions 2.8 and 2.9), which are, roughly speaking, cohomology classes of negative BBF-square whose duals are represented by minimal rational curves on a deformation of
![]() $M$
.
$M$
.
This description is most easy to explain for a K3 surface. In this case, MBM classes are integral classes of self-intersection
![]() $-2$
, commonly called
$-2$
, commonly called
![]() $(-2)$
-classes.
$(-2)$
-classes.
Let
![]() $M$
be a projective K3 surface, and
$M$
be a projective K3 surface, and
![]() $\operatorname{Pos}(M)\subset H^{1,1}(M)$
the positive cone, that is, the one of two connected components of the set
$\operatorname{Pos}(M)\subset H^{1,1}(M)$
the positive cone, that is, the one of two connected components of the set
![]() $\{v\in H^{1,1}(M,\mathbb{R})\mid (v,v)>0\}$
which contains the Kähler classes. Denote by
$\{v\in H^{1,1}(M,\mathbb{R})\mid (v,v)>0\}$
which contains the Kähler classes. Denote by
![]() $R$
the set of all
$R$
the set of all
![]() $(-2)$
-classes on
$(-2)$
-classes on
![]() $M$
, and let
$M$
, and let
![]() $R^{\bot }$
be the union of all orthogonal hyperplanes to all
$R^{\bot }$
be the union of all orthogonal hyperplanes to all
![]() $v\in R$
. Then the Kähler cone
$v\in R$
. Then the Kähler cone
![]() $\operatorname{Kah}(M)$
is one of the connected components of
$\operatorname{Kah}(M)$
is one of the connected components of
![]() $\operatorname{Pos}(M)\backslash R^{\bot }$
, and
$\operatorname{Pos}(M)\backslash R^{\bot }$
, and
This gives an explicit description of the automorphism group, which becomes quite simple when
![]() $\operatorname{Kah}(M)=\operatorname{Pos}(M)$
, and this happens when
$\operatorname{Kah}(M)=\operatorname{Pos}(M)$
, and this happens when
![]() $M$
has no
$M$
has no
![]() $(-2)$
-classes of Hodge type
$(-2)$
-classes of Hodge type
![]() $(1,1)$
. When
$(1,1)$
. When
![]() $\operatorname{Kah}(M)=\operatorname{Pos}(M)$
, the group
$\operatorname{Kah}(M)=\operatorname{Pos}(M)$
, the group
![]() $\operatorname{Aut}(M)$
is identified with the subgroup
$\operatorname{Aut}(M)$
is identified with the subgroup
![]() $\unicode[STIX]{x1D6E4}_{M}\subset \operatorname{SO}^{+}(H^{2}(M,\mathbb{Z}))$
,
$\unicode[STIX]{x1D6E4}_{M}\subset \operatorname{SO}^{+}(H^{2}(M,\mathbb{Z}))$
,
(‘the group of Hodge isometries of
![]() $H^{2}(M,\mathbb{Z})$
’). It is not hard to see that
$H^{2}(M,\mathbb{Z})$
’). It is not hard to see that
![]() $\unicode[STIX]{x1D6E4}_{M}$
is mapped onto a finite-index subgroup of the group of isometries of the Picard lattice
$\unicode[STIX]{x1D6E4}_{M}$
is mapped onto a finite-index subgroup of the group of isometries of the Picard lattice
![]() $\operatorname{Pic}(M)=H^{1,1}(M,\mathbb{Z})$
; hence, it is infinite whenever this lattice has infinite automorphism group. Now
$\operatorname{Pic}(M)=H^{1,1}(M,\mathbb{Z})$
; hence, it is infinite whenever this lattice has infinite automorphism group. Now
![]() $\operatorname{Pic}(M)$
has signature
$\operatorname{Pic}(M)$
has signature
![]() $(1,k)$
by the Hodge index theorem. It is well known (see e.g. [Reference DicksonDic54]) that
$(1,k)$
by the Hodge index theorem. It is well known (see e.g. [Reference DicksonDic54]) that
![]() $\unicode[STIX]{x1D6E4}_{M}$
is infinite when
$\unicode[STIX]{x1D6E4}_{M}$
is infinite when
![]() $k>1$
and also when
$k>1$
and also when
![]() $k=1$
and the Picard lattice does not represent zero (that is, there is no nonzero
$k=1$
and the Picard lattice does not represent zero (that is, there is no nonzero
![]() $v\in \operatorname{Pic}(M)$
with
$v\in \operatorname{Pic}(M)$
with
![]() $v^{2}=0$
).
$v^{2}=0$
).
Therefore, to produce K3 surfaces with infinite automorphism group, it would suffice to find a primitive sublattice of rank
![]() ${\geqslant}3$
, signature
${\geqslant}3$
, signature
![]() $(1,k)$
,
$(1,k)$
,
![]() $k\geqslant 2$
, and without
$k\geqslant 2$
, and without
![]() $(-2)$
-vectors in
$(-2)$
-vectors in
![]() $H^{2}(M,\mathbb{Z})$
. This can be done using the work of Nikulin [Reference NikulinNik80], which implies that any lattice of signature
$H^{2}(M,\mathbb{Z})$
. This can be done using the work of Nikulin [Reference NikulinNik80], which implies that any lattice of signature
![]() $(1,k)$
,
$(1,k)$
,
![]() $k<10$
, admits a primitive embedding to the K3 lattice (that is, an even unimodular lattice of signature (3, 19); such a lattice is unique up to isomorphism and isomorphic to
$k<10$
, admits a primitive embedding to the K3 lattice (that is, an even unimodular lattice of signature (3, 19); such a lattice is unique up to isomorphism and isomorphic to
![]() $H^{2}(M,\mathbb{Z})$
).
$H^{2}(M,\mathbb{Z})$
).
The argument above produces, in particular, symplectic automorphisms, that is, automor- phisms which preserve the holomorphic symplectic structure. Indeed, we can extend isometries of the Neron–Severi lattice to those of
![]() $H^{2}(M,\mathbb{Z})$
by requiring the trivial action on the orthogonal complement (since the orthogonal decomposition is over the rationals, we might have to replace the full group of isometries by a finite-index subgroup).
$H^{2}(M,\mathbb{Z})$
by requiring the trivial action on the orthogonal complement (since the orthogonal decomposition is over the rationals, we might have to replace the full group of isometries by a finite-index subgroup).
This approach is generalized in the present paper. In [Reference Amerik and VerbitskyAV16], it is shown that for each hyperkähler manifold
![]() $M$
there exists
$M$
there exists
![]() $N>0$
, depending only on the deformation class of
$N>0$
, depending only on the deformation class of
![]() $M$
, such that for all MBM classes
$M$
, such that for all MBM classes
![]() $v$
one has
$v$
one has
![]() $-N<q(v,v)<0$
. In the present paper, we prove that the lattice
$-N<q(v,v)<0$
. In the present paper, we prove that the lattice
![]() $H^{2}(M,\mathbb{Z})$
of a hyperkähler manifold
$H^{2}(M,\mathbb{Z})$
of a hyperkähler manifold
![]() $M$
satisfying
$M$
satisfying
![]() $b_{2}(M)\geqslant 5$
(it seems reasonable to believe that this always holds, but no proof exists today) contains a primitive sublattice
$b_{2}(M)\geqslant 5$
(it seems reasonable to believe that this always holds, but no proof exists today) contains a primitive sublattice
![]() $\unicode[STIX]{x1D6EC}\subset H^{2}(M,\mathbb{Z})$
which does not represent numbers smaller than
$\unicode[STIX]{x1D6EC}\subset H^{2}(M,\mathbb{Z})$
which does not represent numbers smaller than
![]() $N$
(that is, for any nonzero
$N$
(that is, for any nonzero
![]() $v\in \unicode[STIX]{x1D6EC}$
, one has
$v\in \unicode[STIX]{x1D6EC}$
, one has
![]() $|q(v,v)|\geqslant N$
). Using the global Torelli theorem, we find a deformation
$|q(v,v)|\geqslant N$
). Using the global Torelli theorem, we find a deformation
![]() $M_{1}$
of
$M_{1}$
of
![]() $M$
with
$M$
with
![]() $\operatorname{Pic}(M_{1})=\unicode[STIX]{x1D6EC}$
. In this case, the Picard lattice of
$\operatorname{Pic}(M_{1})=\unicode[STIX]{x1D6EC}$
. In this case, the Picard lattice of
![]() $M_{1}$
contains no MBM classes, the Kähler cone coincides with the positive cone and the symplectic automorphism group is mapped onto a finite-index subgroup of the isometry group
$M_{1}$
contains no MBM classes, the Kähler cone coincides with the positive cone and the symplectic automorphism group is mapped onto a finite-index subgroup of the isometry group
![]() $O(\unicode[STIX]{x1D6EC})$
(Corollary 2.12).
$O(\unicode[STIX]{x1D6EC})$
(Corollary 2.12).
This allows us to prove the following theorem.
Theorem 1.1. Let
![]() $M$
be a hyperkähler manifold with
$M$
be a hyperkähler manifold with
![]() $b_{2}(M)\geqslant 5$
. Then
$b_{2}(M)\geqslant 5$
. Then
![]() $M$
admits a projective deformation
$M$
admits a projective deformation
![]() $M^{\prime }$
with infinite group of symplectic automorphisms and Picard rank
$M^{\prime }$
with infinite group of symplectic automorphisms and Picard rank
![]() $2$
.
$2$
.
Proof. See Corollary 3.5. ◻
The automorphisms obtained in Theorem 1.1 are hyperbolic or loxodromic: they act on
![]() $H^{1,1}(M)$
with one real eigenvalue
$H^{1,1}(M)$
with one real eigenvalue
![]() $\unicode[STIX]{x1D6FC}>1$
, another
$\unicode[STIX]{x1D6FC}>1$
, another
![]() $\unicode[STIX]{x1D6FC}^{-1}$
and the rest of the eigenvalues have absolute value 1. It is precisely the type of transformation which is the most interesting for dynamics: our automorphisms are of positive entropy.
$\unicode[STIX]{x1D6FC}^{-1}$
and the rest of the eigenvalues have absolute value 1. It is precisely the type of transformation which is the most interesting for dynamics: our automorphisms are of positive entropy.
The symplectic automorphisms of hyperkähler manifolds can be classified according to their action on
![]() $H^{1,1}(M)$
, by the same principle as the automorphisms of the hyperbolic space (see Theorem-Definition 3.2). There are hyperbolic, or loxodromic, automorphisms (the ones which act on
$H^{1,1}(M)$
, by the same principle as the automorphisms of the hyperbolic space (see Theorem-Definition 3.2). There are hyperbolic, or loxodromic, automorphisms (the ones which act on
![]() $H^{1,1}(M)$
with two real eigenvalues of absolute value
$H^{1,1}(M)$
with two real eigenvalues of absolute value
![]() $\neq 1$
), elliptic ones (automorphisms of finite order) and parabolic ones (quasi-unipotent with a nontrivial rank-3 Jordan cell); equivalently, the parabolic automorphisms are those which fix an isotropic vector. This vector must be rational, that is, a class of a Beauville–Bogomolov isotropic line bundle; such a line bundle is nef on a birational model of
$\neq 1$
), elliptic ones (automorphisms of finite order) and parabolic ones (quasi-unipotent with a nontrivial rank-3 Jordan cell); equivalently, the parabolic automorphisms are those which fix an isotropic vector. This vector must be rational, that is, a class of a Beauville–Bogomolov isotropic line bundle; such a line bundle is nef on a birational model of
![]() $M$
and conjecturally its sections give a Lagrangian fibration on that model. The parabolic automorphisms are, thus, conjecturally, those which preserve Lagrangian fibrations, and this is one of the main reasons for our interest in them.
$M$
and conjecturally its sections give a Lagrangian fibration on that model. The parabolic automorphisms are, thus, conjecturally, those which preserve Lagrangian fibrations, and this is one of the main reasons for our interest in them.
If we want to produce a parabolic automorphism of a deformation of a given hyperkähler manifold, more work is necessary. We need to find a primitive sublattice
![]() $\unicode[STIX]{x1D6EC}\subset H^{2}(M,\mathbb{Z})$
of signature
$\unicode[STIX]{x1D6EC}\subset H^{2}(M,\mathbb{Z})$
of signature
![]() $(1,k)$
,
$(1,k)$
,
![]() $k\geqslant 2$
, such that
$k\geqslant 2$
, such that
![]() $q(v,v)\notin ]-N,0[$
for
$q(v,v)\notin ]-N,0[$
for
![]() $v\in \unicode[STIX]{x1D6EC}$
, and
$v\in \unicode[STIX]{x1D6EC}$
, and
![]() $\unicode[STIX]{x1D6EC}$
admits a parabolic isometry. In order to produce such a sublattice, we rely on the classification of rational vector spaces with a quadratic form by the signature, discriminant and the collection of
$\unicode[STIX]{x1D6EC}$
admits a parabolic isometry. In order to produce such a sublattice, we rely on the classification of rational vector spaces with a quadratic form by the signature, discriminant and the collection of
![]() $p$
-adic invariants, and on Nikulin’s work on lattice embeddings. Our method works under a stronger restriction on
$p$
-adic invariants, and on Nikulin’s work on lattice embeddings. Our method works under a stronger restriction on
![]() $b_{2}$
.
$b_{2}$
.
The main problem (and the main reason for the strong restriction on
![]() $b_{2}$
) is that the second cohomology lattice
$b_{2}$
) is that the second cohomology lattice
![]() $H^{2}(M,\mathbb{Z})$
of a hyperkähler manifold
$H^{2}(M,\mathbb{Z})$
of a hyperkähler manifold
![]() $M$
is not necessarily unimodular. In this case, one cannot apply Nikulin’s theorem directly. To construct the sublattice we need, we first embed our lattice
$M$
is not necessarily unimodular. In this case, one cannot apply Nikulin’s theorem directly. To construct the sublattice we need, we first embed our lattice
![]() $H^{2}(M,\mathbb{Z})$
into
$H^{2}(M,\mathbb{Z})$
into
![]() $H_{\mathbb{Q}}:=H\otimes _{\mathbb{Z}}\mathbb{Q}$
, where
$H_{\mathbb{Q}}:=H\otimes _{\mathbb{Z}}\mathbb{Q}$
, where
![]() $H$
is a unimodular lattice. Then we apply Nikulin’s theorem to
$H$
is a unimodular lattice. Then we apply Nikulin’s theorem to
![]() $H$
, obtaining a primitive sublattice
$H$
, obtaining a primitive sublattice
![]() $\unicode[STIX]{x1D6EC}\subset H$
, and take the intersection of
$\unicode[STIX]{x1D6EC}\subset H$
, and take the intersection of
![]() $\unicode[STIX]{x1D6EC}$
with the image of
$\unicode[STIX]{x1D6EC}$
with the image of
![]() $H^{2}(M,\mathbb{Z})\subset H_{\mathbb{Q}}$
. This is no longer primitive in
$H^{2}(M,\mathbb{Z})\subset H_{\mathbb{Q}}$
. This is no longer primitive in
![]() $H^{2}(M,\mathbb{Z})$
, but we have a good control over the extent to which it is not, sufficient to assure that the ‘primitivization’ does not have vectors of small nonzero square.
$H^{2}(M,\mathbb{Z})$
, but we have a good control over the extent to which it is not, sufficient to assure that the ‘primitivization’ does not have vectors of small nonzero square.
Theorem 1.2. Let
![]() $M$
be a hyperkähler manifold with
$M$
be a hyperkähler manifold with
![]() $b_{2}(M)\geqslant 14$
. Then
$b_{2}(M)\geqslant 14$
. Then
![]() $M$
has a deformation with
$M$
has a deformation with
![]() $\operatorname{rk}\operatorname{Pic}(M)\geqslant 3$
such that its group of symplectic automorphisms contains a parabolic element.
$\operatorname{rk}\operatorname{Pic}(M)\geqslant 3$
such that its group of symplectic automorphisms contains a parabolic element.
Proof. See Corollary 3.10. ◻
Remark 1.3. Using the main result of [Reference VerbitskyVer15], one sees that under the conditions of each of the two theorems, the points corresponding to hyperkähler manifolds with a hyperbolic (respectively parabolic) automorphism are dense in the Teichmüller space.
2 Hyperkähler manifolds: basic results
In this section, we recall the definitions and basic properties of hyperkähler manifolds and MBM classes.
2.1 Hyperkähler manifolds
Definition 2.1. A hyperkähler manifold
![]() $M$
, that is, a compact Kähler holomorphically symplectic manifold, is called a simple or a maximal holonomy hyperkähler manifold (alternatively, an irreducible holomorphically symplectic manifold (IHSM)) if
$M$
, that is, a compact Kähler holomorphically symplectic manifold, is called a simple or a maximal holonomy hyperkähler manifold (alternatively, an irreducible holomorphically symplectic manifold (IHSM)) if
![]() $\unicode[STIX]{x1D70B}_{1}(M)=0$
and
$\unicode[STIX]{x1D70B}_{1}(M)=0$
and
![]() $H^{2,0}(M)=\mathbb{C}$
.
$H^{2,0}(M)=\mathbb{C}$
.
This definition is motivated by the following theorem of Bogomolov.
Theorem 2.2 [Reference BogomolovBog74].
Any hyperkähler manifold admits a finite covering which is a product of a torus and several simple hyperkähler manifolds.
Remark 2.3. Further on, we shall tacitly assume that the hyperkähler manifolds we consider are of maximal holonomy (simple, IHSM).
The second cohomology
![]() $H^{2}(M,\mathbb{Z})$
of a simple hyperkähler manifold
$H^{2}(M,\mathbb{Z})$
of a simple hyperkähler manifold
![]() $M$
carries a primitive integral quadratic form
$M$
carries a primitive integral quadratic form
![]() $q$
, called the Bogomolov–Beauville–Fujiki (BBF) form. It generalizes the intersection product on a K3 surface: its signature is
$q$
, called the Bogomolov–Beauville–Fujiki (BBF) form. It generalizes the intersection product on a K3 surface: its signature is
![]() $(3,b_{2}-3)$
on
$(3,b_{2}-3)$
on
![]() $H^{2}(M,\mathbb{R})$
and
$H^{2}(M,\mathbb{R})$
and
![]() $(1,b_{2}-3)$
on
$(1,b_{2}-3)$
on
![]() $H_{\mathbb{R}}^{1,1}(M)$
. It was first defined in [Reference BogomolovBog78] and [Reference BeauvilleBea83], but it is easiest to describe it using the Fujiki theorem, proved in [Reference FujikiFuj87] and stressing the topological nature of the form.
$H_{\mathbb{R}}^{1,1}(M)$
. It was first defined in [Reference BogomolovBog78] and [Reference BeauvilleBea83], but it is easiest to describe it using the Fujiki theorem, proved in [Reference FujikiFuj87] and stressing the topological nature of the form.
Theorem 2.4 (Fujiki).
Let
![]() $M$
be a simple hyperkähler manifold,
$M$
be a simple hyperkähler manifold,
![]() $\unicode[STIX]{x1D702}\in H^{2}(M)$
and
$\unicode[STIX]{x1D702}\in H^{2}(M)$
and
![]() $n=\frac{1}{2}\dim M$
. Then
$n=\frac{1}{2}\dim M$
. Then
![]() $\int _{M}\unicode[STIX]{x1D702}^{2n}=cq(\unicode[STIX]{x1D702},\unicode[STIX]{x1D702})^{n}$
, where
$\int _{M}\unicode[STIX]{x1D702}^{2n}=cq(\unicode[STIX]{x1D702},\unicode[STIX]{x1D702})^{n}$
, where
![]() $q$
is a primitive integral nondegenerate quadratic form on
$q$
is a primitive integral nondegenerate quadratic form on
![]() $H^{2}(M,\mathbb{Z})$
, and
$H^{2}(M,\mathbb{Z})$
, and
![]() $c>0$
is a rational number depending only on
$c>0$
is a rational number depending only on
![]() $M$
.
$M$
.
Consider
![]() $M$
as a differentiable manifold and denote by
$M$
as a differentiable manifold and denote by
![]() $I$
our complex structure on
$I$
our complex structure on
![]() $M$
(we shall use notation like
$M$
(we shall use notation like
![]() $\operatorname{Pic}(M,I)$
,
$\operatorname{Pic}(M,I)$
,
![]() $H^{1,1}(M,I)$
etc. to stress that we are working with this particular complex structure). We call the Teichmüller space
$H^{1,1}(M,I)$
etc. to stress that we are working with this particular complex structure). We call the Teichmüller space
![]() $\mathsf{Teich}$
the quotient
$\mathsf{Teich}$
the quotient
![]() $\mathsf{Comp}(M)/\mathsf{Diff}_{0}(M)$
, where
$\mathsf{Comp}(M)/\mathsf{Diff}_{0}(M)$
, where
![]() $\mathsf{Comp}(M)$
denotes the space of all complex structures of Kähler type on
$\mathsf{Comp}(M)$
denotes the space of all complex structures of Kähler type on
![]() $M$
and
$M$
and
![]() $\mathsf{Diff}_{0}(M)$
is the group of isotopies. It follows from a result of Huybrechts (see [Reference HuybrechtsHuy03]) that for an IHSM
$\mathsf{Diff}_{0}(M)$
is the group of isotopies. It follows from a result of Huybrechts (see [Reference HuybrechtsHuy03]) that for an IHSM
![]() $M$
,
$M$
,
![]() $\mathsf{Teich}$
has only finitely many connected components. Let
$\mathsf{Teich}$
has only finitely many connected components. Let
![]() $\mathsf{Teich}_{I}$
denote the one containing our given complex structure
$\mathsf{Teich}_{I}$
denote the one containing our given complex structure
![]() $I$
. Consider the subgroup of the mapping class group
$I$
. Consider the subgroup of the mapping class group
![]() $\mathsf{Diff}(M)/\mathsf{Diff}_{0}(M)$
fixing
$\mathsf{Diff}(M)/\mathsf{Diff}_{0}(M)$
fixing
![]() $\mathsf{Teich}_{I}$
.
$\mathsf{Teich}_{I}$
.
Definition 2.5. The monodromy group
![]() $\mathsf{Mon}(M)$
is the image of this subgroup in
$\mathsf{Mon}(M)$
is the image of this subgroup in
![]() $O(H^{2}(M,\mathbb{Z}),q)$
. The Hodge monodromy group
$O(H^{2}(M,\mathbb{Z}),q)$
. The Hodge monodromy group
![]() $\mathsf{Mon}_{I}(M)$
is the subgroup of
$\mathsf{Mon}_{I}(M)$
is the subgroup of
![]() $\mathsf{Mon}(M)$
preserving the Hodge decomposition.
$\mathsf{Mon}(M)$
preserving the Hodge decomposition.
Theorem 2.6 [Reference VerbitskyVer13, Theorem 3.5].
The monodromy group is a finite-index subgroup in
![]() $O(H^{2}(M,\mathbb{Z}),q)$
.
$O(H^{2}(M,\mathbb{Z}),q)$
.
The image of the Hodge monodromy is therefore an arithmetic subgroup of the orthogonal group of the Picard lattice
![]() $\operatorname{Pic}(M,I)$
. Notice that the action of
$\operatorname{Pic}(M,I)$
. Notice that the action of
![]() $\mathsf{Mon}_{I}(M)$
on the Picard lattice can have a kernel; when
$\mathsf{Mon}_{I}(M)$
on the Picard lattice can have a kernel; when
![]() $(M,I)$
is projective, it is easy to see that the kernel is a finite group (just use the fact that it fixes a Kähler class and therefore consists of isometries), but it can be infinite in general [Reference McMullenMcM02]. By a slight abuse of notation, we sometimes also call the Hodge monodromy this arithmetic subgroup itself; one way to avoid such an abuse is to introduce the symplectic Hodge monodromy group
$(M,I)$
is projective, it is easy to see that the kernel is a finite group (just use the fact that it fixes a Kähler class and therefore consists of isometries), but it can be infinite in general [Reference McMullenMcM02]. By a slight abuse of notation, we sometimes also call the Hodge monodromy this arithmetic subgroup itself; one way to avoid such an abuse is to introduce the symplectic Hodge monodromy group
![]() $\mathsf{Mon}_{I,\unicode[STIX]{x1D6FA}}(M)$
, which is a subgroup of
$\mathsf{Mon}_{I,\unicode[STIX]{x1D6FA}}(M)$
, which is a subgroup of
![]() $\mathsf{Mon}_{I}(M)$
fixing the symplectic form
$\mathsf{Mon}_{I}(M)$
fixing the symplectic form
![]() $\unicode[STIX]{x1D6FA}$
. Its representation on the Picard lattice is faithful and the image is of finite index in that of
$\unicode[STIX]{x1D6FA}$
. Its representation on the Picard lattice is faithful and the image is of finite index in that of
![]() $\mathsf{Mon}_{I}(M)$
, so that
$\mathsf{Mon}_{I}(M)$
, so that
![]() $\mathsf{Mon}_{I,\unicode[STIX]{x1D6FA}}(M)$
is identified to an arithmetic subgroup of
$\mathsf{Mon}_{I,\unicode[STIX]{x1D6FA}}(M)$
is identified to an arithmetic subgroup of
![]() $O(\operatorname{Pic}(M,I),q)$
.
$O(\operatorname{Pic}(M,I),q)$
.
Theorem 2.7 (Markman’s Hodge-theoretic Torelli theorem [Reference MarkmanMar11]).
The image of
![]() $\operatorname{Aut}(M,I)$
acting on
$\operatorname{Aut}(M,I)$
acting on
![]() $H^{2}(M)$
is the subgroup of
$H^{2}(M)$
is the subgroup of
![]() $\mathsf{Mon}_{I}(M)$
preserving the Kähler cone
$\mathsf{Mon}_{I}(M)$
preserving the Kähler cone
![]() $\operatorname{Kah}(M,I)$
.
$\operatorname{Kah}(M,I)$
.
In this paper, we construct hyperkähler manifolds with the Kähler cone equal to the positive cone, and use this construction to find manifolds admitting interesting automorphisms of infinite order.
2.2 MBM classes
We call a cohomology class
![]() $\unicode[STIX]{x1D702}\in H^{2}(M,\mathbb{R})$
positive if
$\unicode[STIX]{x1D702}\in H^{2}(M,\mathbb{R})$
positive if
![]() $q(\unicode[STIX]{x1D702},\unicode[STIX]{x1D702})>0$
, and negative if
$q(\unicode[STIX]{x1D702},\unicode[STIX]{x1D702})>0$
, and negative if
![]() $q(\unicode[STIX]{x1D702},\unicode[STIX]{x1D702})<0$
. The positive cone
$q(\unicode[STIX]{x1D702},\unicode[STIX]{x1D702})<0$
. The positive cone
![]() $\operatorname{Pos}(M,I)\in H_{\mathbb{R}}^{1,1}(M,I)$
is the connected component of the set of positive classes on
$\operatorname{Pos}(M,I)\in H_{\mathbb{R}}^{1,1}(M,I)$
is the connected component of the set of positive classes on
![]() $M$
which contains the Kähler classes. The Kähler cone is cut out inside the positive cone by a certain, possibly infinite, number of rational hyperplanes (by a result of Huybrechts, we may take for these the orthogonals to the classes of rational curves).
$M$
which contains the Kähler classes. The Kähler cone is cut out inside the positive cone by a certain, possibly infinite, number of rational hyperplanes (by a result of Huybrechts, we may take for these the orthogonals to the classes of rational curves).
In [Reference Amerik and VerbitskyAV15], we have introduced the following notion.
Definition 2.8. An integral
![]() $(1,1)$
-class
$(1,1)$
-class
![]() $z$
on
$z$
on
![]() $(M,I)$
is called monodromy birationally minimal (MBM) if for some
$(M,I)$
is called monodromy birationally minimal (MBM) if for some
![]() $\unicode[STIX]{x1D6FE}\in \mathsf{Mon}_{I}(M)$
, the hyperplane
$\unicode[STIX]{x1D6FE}\in \mathsf{Mon}_{I}(M)$
, the hyperplane
![]() $\unicode[STIX]{x1D6FE}(z)^{\bot }$
supports a (maximal-dimensional) face of the Kähler cone of a birational model of
$\unicode[STIX]{x1D6FE}(z)^{\bot }$
supports a (maximal-dimensional) face of the Kähler cone of a birational model of
![]() $(M,I)$
.
$(M,I)$
.
We have shown in [Reference Amerik and VerbitskyAV15] the invariance of the MBM property under all deformations of complex structure which leave
![]() $z$
of type
$z$
of type
![]() $(1,1)$
. Moreover, we have observed that a negative class
$(1,1)$
. Moreover, we have observed that a negative class
![]() $z$
generating the Picard group
$z$
generating the Picard group
![]() $\operatorname{Pic}(M,I)$
is MBM if and only if a rational multiple of
$\operatorname{Pic}(M,I)$
is MBM if and only if a rational multiple of
![]() $z$
is represented by a curve (in fact automatically rational; when we speak about curves representing
$z$
is represented by a curve (in fact automatically rational; when we speak about curves representing
![]() $(1,1)$
-classes in cohomology, it means that we identify the integral classes of curves to certain rational
$(1,1)$
-classes in cohomology, it means that we identify the integral classes of curves to certain rational
![]() $(1,1)$
-classes by the obvious isomorphism provided by the BBF form). This leads to a simple extension of the notion to the classes in the whole
$(1,1)$
-classes by the obvious isomorphism provided by the BBF form). This leads to a simple extension of the notion to the classes in the whole
![]() $H^{2}(M,\mathbb{Z})$
rather than the Picard lattice. By writing
$H^{2}(M,\mathbb{Z})$
rather than the Picard lattice. By writing
![]() $M$
rather than
$M$
rather than
![]() $(M,I)$
, we let a complex structure
$(M,I)$
, we let a complex structure
![]() $I$
vary in its deformation class; this class is not uniquely determined by the topology, but there are finitely many of them by the already mentioned finiteness result of Huybrechts [Reference HuybrechtsHuy03].
$I$
vary in its deformation class; this class is not uniquely determined by the topology, but there are finitely many of them by the already mentioned finiteness result of Huybrechts [Reference HuybrechtsHuy03].
Definition 2.9. A negative class
![]() $z\in H^{2}(M,\mathbb{Z})$
on a hyperkähler manifold is called an MBM class if there exists a deformation of
$z\in H^{2}(M,\mathbb{Z})$
on a hyperkähler manifold is called an MBM class if there exists a deformation of
![]() $M$
with
$M$
with
![]() $\operatorname{Pic}(M)=\langle z\rangle$
such that
$\operatorname{Pic}(M)=\langle z\rangle$
such that
![]() $\unicode[STIX]{x1D706}z$
is represented by a curve for some
$\unicode[STIX]{x1D706}z$
is represented by a curve for some
![]() $\unicode[STIX]{x1D706}\neq 0$
.
$\unicode[STIX]{x1D706}\neq 0$
.
Theorem 2.10 [Reference Amerik and VerbitskyAV15, § 6].
Let
![]() $(M,I)$
be a hyperkähler manifold, and
$(M,I)$
be a hyperkähler manifold, and
![]() $S$
the set of all its MBM classes of type
$S$
the set of all its MBM classes of type
![]() $(1,1)$
. The Kähler cone of
$(1,1)$
. The Kähler cone of
![]() $(M,I)$
is a connected component of
$(M,I)$
is a connected component of
![]() $\operatorname{Pos}(M,I)\backslash \bigcup _{z\in S}z^{\bot }$
.
$\operatorname{Pos}(M,I)\backslash \bigcup _{z\in S}z^{\bot }$
.
Remark 2.11. As follows from an observation by Markman, the other connected components (‘the Kähler chambers’) are the monodromy transforms of the Kähler cones of birational models of
![]() $(M,I)$
. The Hodge monodromy group permutes the Kähler chambers.
$(M,I)$
. The Hodge monodromy group permutes the Kähler chambers.
From Theorem 2.10 and the Hodge-theoretic Torelli theorem, we easily deduce the following result.
Corollary 2.12. Let
![]() $(M,I)$
be a hyperkähler manifold which has no MBM classes of type
$(M,I)$
be a hyperkähler manifold which has no MBM classes of type
![]() $(1,1)$
. Then any element of
$(1,1)$
. Then any element of
![]() $\mathsf{Mon}_{I}(M)$
lifts to an automorphism of
$\mathsf{Mon}_{I}(M)$
lifts to an automorphism of
![]() $(M,I)$
.
$(M,I)$
.
Proof. Indeed, for such manifolds
![]() $\operatorname{Kah}(M,I)=\operatorname{Pos}(M,I)$
and therefore the whole group
$\operatorname{Kah}(M,I)=\operatorname{Pos}(M,I)$
and therefore the whole group
![]() $\mathsf{Mon}_{I}(M)$
preserves the Kähler cone.◻
$\mathsf{Mon}_{I}(M)$
preserves the Kähler cone.◻
2.3 Morrison–Kawamata cone conjecture, MBM bound and automorphisms
The following theorem has been proved in [Reference Amerik and VerbitskyAV14].
Theorem 2.13 [Reference Amerik and VerbitskyAV14].
Suppose that
![]() $(M,I)$
is projective and the Picard number
$(M,I)$
is projective and the Picard number
![]() $\unicode[STIX]{x1D70C}(M,I)>3$
. Then the Hodge monodromy group has only finitely many orbits on the set of MBM classes of type
$\unicode[STIX]{x1D70C}(M,I)>3$
. Then the Hodge monodromy group has only finitely many orbits on the set of MBM classes of type
![]() $(1,1)$
on
$(1,1)$
on
![]() $M$
.
$M$
.
This result is a version of the Morrison–Kawamata cone conjecture for hyperkähler manifolds. Its proof is based on ideas of homogeneous dynamics (Ratner theory and Dani–Margulis and Mozes–Shah theorems).
Since the Hodge monodromy group acts by isometries, it follows that the primitive MBM classes in
![]() $H^{1,1}(M)$
have bounded square. Using deformations, one actually obtains the boundedness without the projectivity assumption and with the condition
$H^{1,1}(M)$
have bounded square. Using deformations, one actually obtains the boundedness without the projectivity assumption and with the condition
![]() $\unicode[STIX]{x1D70C}(M,I)>3$
replaced by
$\unicode[STIX]{x1D70C}(M,I)>3$
replaced by
![]() $b_{2}(M)>5$
. One of the main tools of this paper is a subsequent generalization of this statement.
$b_{2}(M)>5$
. One of the main tools of this paper is a subsequent generalization of this statement.
Theorem 2.14 [Reference Amerik and VerbitskyAV16].
Let
![]() $M$
be a hyperkähler manifold with
$M$
be a hyperkähler manifold with
![]() $b_{2}\geqslant 5$
. Then there exists a number
$b_{2}\geqslant 5$
. Then there exists a number
![]() $N>0$
, called the MBM bound, depending only on deformation type of
$N>0$
, called the MBM bound, depending only on deformation type of
![]() $M$
, such that any MBM class
$M$
, such that any MBM class
![]() $z$
satisfies
$z$
satisfies
![]() $|q(z,z)|<N$
.
$|q(z,z)|<N$
.
Remark 2.15. In fact, there is even a bound depending only on the topology of
![]() $M$
, as the Teichmüller space for hyperkähler manifolds has only finitely many connected components and there are only finitely many smooth structures on a compact topological manifold of dimension 5 or more.
$M$
, as the Teichmüller space for hyperkähler manifolds has only finitely many connected components and there are only finitely many smooth structures on a compact topological manifold of dimension 5 or more.
Remark 2.16. For projective manifolds of K3 type, such a bound has been obtained by Bayer et al. [Reference Bayer, Hassett and TschinkelBHT15]; Hassett and Tschinkel have also formulated a number of related conjectures in their series of works on the subject.
Let us explain how this theorem permits one to construct hyperkähler manifolds with large automorphism groups.
Definition 2.17. A lattice, or a quadratic lattice, is a free abelian group
![]() $\unicode[STIX]{x1D6EC}\cong \mathbb{Z}^{n}$
equipped with an integer-valued quadratic form
$\unicode[STIX]{x1D6EC}\cong \mathbb{Z}^{n}$
equipped with an integer-valued quadratic form
![]() $q$
. When we speak of an embedding of lattices, we always assume that it is compatible with their quadratic forms.
$q$
. When we speak of an embedding of lattices, we always assume that it is compatible with their quadratic forms.
Definition 2.18. A sublattice
![]() $\unicode[STIX]{x1D6EC}^{\prime }\subset \unicode[STIX]{x1D6EC}$
is called primitive if
$\unicode[STIX]{x1D6EC}^{\prime }\subset \unicode[STIX]{x1D6EC}$
is called primitive if
![]() $\unicode[STIX]{x1D6EC}/\unicode[STIX]{x1D6EC}^{\prime }$
is torsion-free. A number
$\unicode[STIX]{x1D6EC}/\unicode[STIX]{x1D6EC}^{\prime }$
is torsion-free. A number
![]() $a$
is represented by a lattice
$a$
is represented by a lattice
![]() $(\unicode[STIX]{x1D6EC},q)$
if
$(\unicode[STIX]{x1D6EC},q)$
if
![]() $a=q(x,x)$
for some nonzero
$a=q(x,x)$
for some nonzero
![]() $x\in \unicode[STIX]{x1D6EC}$
.
$x\in \unicode[STIX]{x1D6EC}$
.
Now let
![]() $M$
be a hyperkähler manifold. Consider the lattice
$M$
be a hyperkähler manifold. Consider the lattice
![]() $H^{2}(M,\mathbb{Z})$
equipped with the BBF form
$H^{2}(M,\mathbb{Z})$
equipped with the BBF form
![]() $q$
. By the Torelli theorem, for any primitive sublattice
$q$
. By the Torelli theorem, for any primitive sublattice
![]() $\unicode[STIX]{x1D6EC}\subset H^{2}(M,\mathbb{Z})$
of signature
$\unicode[STIX]{x1D6EC}\subset H^{2}(M,\mathbb{Z})$
of signature
![]() $(1,k)$
, there exists a complex structure
$(1,k)$
, there exists a complex structure
![]() $I$
such that
$I$
such that
![]() $\unicode[STIX]{x1D6EC}=\operatorname{Pic}(M,I)$
is the Picard lattice of
$\unicode[STIX]{x1D6EC}=\operatorname{Pic}(M,I)$
is the Picard lattice of
![]() $(M,I)$
. The key remark is that as soon as we succeed in finding such a primitive sublattice which does not represent small nonzero numbers, the corresponding hyperkähler manifold has fairly large automorphism group.
$(M,I)$
. The key remark is that as soon as we succeed in finding such a primitive sublattice which does not represent small nonzero numbers, the corresponding hyperkähler manifold has fairly large automorphism group.
Theorem 2.19. Let
![]() $M$
be a hyperkähler manifold, and
$M$
be a hyperkähler manifold, and
![]() $\unicode[STIX]{x1D6EC}\subset H^{2}(M,\mathbb{Z})$
a primitive sublattice of signature
$\unicode[STIX]{x1D6EC}\subset H^{2}(M,\mathbb{Z})$
a primitive sublattice of signature
![]() $(1,k)$
which does not represent any number
$(1,k)$
which does not represent any number
![]() $a,0\leqslant |a|\leqslant N$
, where
$a,0\leqslant |a|\leqslant N$
, where
![]() $N$
is the MBM bound (we sometimes say in this case that
$N$
is the MBM bound (we sometimes say in this case that
![]() $\unicode[STIX]{x1D6EC}$
‘satisfies the MBM bound’). Let
$\unicode[STIX]{x1D6EC}$
‘satisfies the MBM bound’). Let
![]() $(M,I)$
be a deformation of
$(M,I)$
be a deformation of
![]() $M$
such that
$M$
such that
![]() $\unicode[STIX]{x1D6EC}=\operatorname{Pic}(M,I)$
. Then the Kähler cone of
$\unicode[STIX]{x1D6EC}=\operatorname{Pic}(M,I)$
. Then the Kähler cone of
![]() $(M,I)$
is equal to the positive cone and the group of holomorphic symplectic automorphisms
$(M,I)$
is equal to the positive cone and the group of holomorphic symplectic automorphisms
![]() $\operatorname{Aut}(M,\unicode[STIX]{x1D6FA})$
is projected with finite kernel onto
$\operatorname{Aut}(M,\unicode[STIX]{x1D6FA})$
is projected with finite kernel onto
![]() $\mathsf{Mon}_{I,\unicode[STIX]{x1D6FA}}(M)$
, which is a subgroup of finite index in
$\mathsf{Mon}_{I,\unicode[STIX]{x1D6FA}}(M)$
, which is a subgroup of finite index in
![]() $O(\unicode[STIX]{x1D6EC})$
.
$O(\unicode[STIX]{x1D6EC})$
.
Proof. For the finiteness of the kernel of the natural map from
![]() $\operatorname{Aut}(M,\unicode[STIX]{x1D6FA})$
to
$\operatorname{Aut}(M,\unicode[STIX]{x1D6FA})$
to
![]() $\mathsf{Mon}_{I,\unicode[STIX]{x1D6FA}}(M)\subset \text{GL}(H^{2}(M))$
, see e.g. [Reference VerbitskyVer13]. Since
$\mathsf{Mon}_{I,\unicode[STIX]{x1D6FA}}(M)\subset \text{GL}(H^{2}(M))$
, see e.g. [Reference VerbitskyVer13]. Since
![]() $\unicode[STIX]{x1D6EC}=H_{I}^{1,1}(M,\mathbb{Z})$
satisfies the MBM bound, it contains no MBM classes, so the Kähler cone is equal to the positive cone. By Corollary 2.12,
$\unicode[STIX]{x1D6EC}=H_{I}^{1,1}(M,\mathbb{Z})$
satisfies the MBM bound, it contains no MBM classes, so the Kähler cone is equal to the positive cone. By Corollary 2.12,
![]() $\operatorname{Aut}(M,\unicode[STIX]{x1D6FA})$
maps onto
$\operatorname{Aut}(M,\unicode[STIX]{x1D6FA})$
maps onto
![]() $\mathsf{Mon}_{I,\unicode[STIX]{x1D6FA}}(M)$
. Now
$\mathsf{Mon}_{I,\unicode[STIX]{x1D6FA}}(M)$
. Now
![]() $\mathsf{Mon}_{I,\unicode[STIX]{x1D6FA}}(M)$
is a finite-index subgroup in
$\mathsf{Mon}_{I,\unicode[STIX]{x1D6FA}}(M)$
is a finite-index subgroup in
![]() $O(\unicode[STIX]{x1D6EC})$
, as follows from Theorem 2.6 and the discussion thereafter.◻
$O(\unicode[STIX]{x1D6EC})$
, as follows from Theorem 2.6 and the discussion thereafter.◻
3 Sublattices and automorphisms
3.1 Classification of automorphisms of a hyperbolic space
The group
![]() $O(m,n),m,n>0$
has four connected components. We denote the connected component of the unity by
$O(m,n),m,n>0$
has four connected components. We denote the connected component of the unity by
![]() $\operatorname{SO}^{+}(m,n)$
.
$\operatorname{SO}^{+}(m,n)$
.
Definition 3.1. Let
![]() $V$
be a real vector space with a quadratic form
$V$
be a real vector space with a quadratic form
![]() $q$
of signature
$q$
of signature
![]() $(1,n)$
. The cone of positive vectors, or positive cone of
$(1,n)$
. The cone of positive vectors, or positive cone of
![]() $V$
, is
$V$
, is
![]() $\operatorname{Pos}(V)=\{x\in V\mid q(x,x)>0\}$
. We denote by
$\operatorname{Pos}(V)=\{x\in V\mid q(x,x)>0\}$
. We denote by
![]() $\mathbb{P}^{+}V$
the projectivization of
$\mathbb{P}^{+}V$
the projectivization of
![]() $\operatorname{Pos}(V)$
.
$\operatorname{Pos}(V)$
.
The space
![]() $\mathbb{P}^{+}V$
is naturally equipped with a hyperbolic metric, so that the hyperbolic geometry suggests the following terminology for elements of
$\mathbb{P}^{+}V$
is naturally equipped with a hyperbolic metric, so that the hyperbolic geometry suggests the following terminology for elements of
![]() $\operatorname{SO}^{+}(V)$
as those induce isometries of
$\operatorname{SO}^{+}(V)$
as those induce isometries of
![]() $\mathbb{P}^{+}V$
.
$\mathbb{P}^{+}V$
.
Theorem-Definition 3.2 (Classification of isometries of
 $\mathbb{P}^{+}V$
).
$\mathbb{P}^{+}V$
).
Let
![]() $n>0$
and
$n>0$
and
![]() $\unicode[STIX]{x1D6FC}\in \operatorname{SO}^{+}(V)$
. Then one and only one of these three cases occurs:
$\unicode[STIX]{x1D6FC}\in \operatorname{SO}^{+}(V)$
. Then one and only one of these three cases occurs:
-
(i)
 $\unicode[STIX]{x1D6FC}$
has an eigenvector
$\unicode[STIX]{x1D6FC}$
has an eigenvector
 $x$
with
$x$
with
 $q(x,x)>0$
(
$q(x,x)>0$
(
 $\unicode[STIX]{x1D6FC}$
is ‘an elliptic isometry’);
$\unicode[STIX]{x1D6FC}$
is ‘an elliptic isometry’); -
(ii)
 $\unicode[STIX]{x1D6FC}$
has an eigenvector
$\unicode[STIX]{x1D6FC}$
has an eigenvector
 $x$
with
$x$
with
 $q(x,x)=0$
and real eigenvalue
$q(x,x)=0$
and real eigenvalue
 $\unicode[STIX]{x1D706}_{x}$
satisfying
$\unicode[STIX]{x1D706}_{x}$
satisfying
 $|\unicode[STIX]{x1D706}_{x}|>1$
(
$|\unicode[STIX]{x1D706}_{x}|>1$
(
 $\unicode[STIX]{x1D6FC}$
is a ‘hyperbolic’ or ‘loxodromic’ isometry);
$\unicode[STIX]{x1D6FC}$
is a ‘hyperbolic’ or ‘loxodromic’ isometry); -
(iii)
 $\unicode[STIX]{x1D6FC}$
has a unique eigenvector
$\unicode[STIX]{x1D6FC}$
has a unique eigenvector
 $x$
with
$x$
with
 $q(x,x)=0$
and eigenvalue 1, and no fixed points on
$q(x,x)=0$
and eigenvalue 1, and no fixed points on
 $\mathbb{P}^{+}V$
(
$\mathbb{P}^{+}V$
(
 $\unicode[STIX]{x1D6FC}$
is a ‘parabolic isometry’).
$\unicode[STIX]{x1D6FC}$
is a ‘parabolic isometry’).
Proof. This is a standard textbook result; see, for instance, [Reference Kapovich and KapranovKap07]. ◻
Definition 3.3. Recall that the BBF form has signature
![]() $(1,b_{2}-3)$
on
$(1,b_{2}-3)$
on
![]() $H^{1,1}(M)$
. An automorphism of a hyperkähler manifold
$H^{1,1}(M)$
. An automorphism of a hyperkähler manifold
![]() $(M,I)$
is called elliptic (parabolic, hyperbolic) if it is elliptic (parabolic, hyperbolic) on
$(M,I)$
is called elliptic (parabolic, hyperbolic) if it is elliptic (parabolic, hyperbolic) on
![]() $H_{I}^{1,1}(M,\mathbb{R})$
.
$H_{I}^{1,1}(M,\mathbb{R})$
.
3.2 Rank-2 sublattices and existence of hyperbolic automorphisms
In this section, we prove the following theorem.
Theorem 3.4. Let
![]() $L$
be a nondegenerate indefinite lattice of rank
$L$
be a nondegenerate indefinite lattice of rank
![]() ${\geqslant}5$
, and
${\geqslant}5$
, and
![]() $N$
a natural number. Then
$N$
a natural number. Then
![]() $L$
contains a primitive rank-
$L$
contains a primitive rank-
![]() $2$
sublattice
$2$
sublattice
![]() $\unicode[STIX]{x1D6EC}$
of signature
$\unicode[STIX]{x1D6EC}$
of signature
![]() $(1,1)$
which does not represent numbers of absolute value less than
$(1,1)$
which does not represent numbers of absolute value less than
![]() $N$
.
$N$
.
This theorem immediately gives examples of hyperkähler manifolds with hyperbolic automorphisms.
Corollary 3.5. Let
![]() $M$
be a hyperkähler manifold with
$M$
be a hyperkähler manifold with
![]() $b_{2}(M)\geqslant 5$
. Then
$b_{2}(M)\geqslant 5$
. Then
![]() $M$
has a deformation admitting a hyperbolic automorphism.
$M$
has a deformation admitting a hyperbolic automorphism.
Proof. Consider the lattice
![]() $L=H^{2}(M,\mathbb{Z})$
and let
$L=H^{2}(M,\mathbb{Z})$
and let
![]() $N$
be the MBM bound for deformations of
$N$
be the MBM bound for deformations of
![]() $M$
. Take a sublattice
$M$
. Take a sublattice
![]() $\unicode[STIX]{x1D6EC}$
as in Theorem 3.4 and a deformation of
$\unicode[STIX]{x1D6EC}$
as in Theorem 3.4 and a deformation of
![]() $M$
such that
$M$
such that
![]() $\unicode[STIX]{x1D6EC}=H_{I}^{1,1}(M,\mathbb{Z})$
. Up to a finite index (meaning that the natural maps between these groups have finite kernel and image of finite index),
$\unicode[STIX]{x1D6EC}=H_{I}^{1,1}(M,\mathbb{Z})$
. Up to a finite index (meaning that the natural maps between these groups have finite kernel and image of finite index),
![]() $\operatorname{Aut}(M)=\mathsf{Mon}_{I}(M)=O(\unicode[STIX]{x1D6EC})$
. But
$\operatorname{Aut}(M)=\mathsf{Mon}_{I}(M)=O(\unicode[STIX]{x1D6EC})$
. But
![]() $\unicode[STIX]{x1D6EC}$
does not represent zero, and then it is well known that
$\unicode[STIX]{x1D6EC}$
does not represent zero, and then it is well known that
![]() $O(\unicode[STIX]{x1D6EC})$
has a hyperbolic element (one way to view this is to interpret
$O(\unicode[STIX]{x1D6EC})$
has a hyperbolic element (one way to view this is to interpret
![]() $\unicode[STIX]{x1D6EC}$
, up to a finite index, as a ring of integers in a real quadratic extension of
$\unicode[STIX]{x1D6EC}$
, up to a finite index, as a ring of integers in a real quadratic extension of
![]() $\mathbb{Q}$
, and notice that the units provide automorphisms; so there is an automorphism of infinite order, and it must automatically be hyperbolic).◻
$\mathbb{Q}$
, and notice that the units provide automorphisms; so there is an automorphism of infinite order, and it must automatically be hyperbolic).◻
To prove Theorem 3.4, we need the following proposition.
Proposition 3.6. Let
![]() $\unicode[STIX]{x1D6EC}$
be a diagonal rank-
$\unicode[STIX]{x1D6EC}$
be a diagonal rank-
![]() $2$
lattice with diagonal entries
$2$
lattice with diagonal entries
![]() $\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}$
divisible by an odd power of
$\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}$
divisible by an odd power of
![]() $p$
, so that
$p$
, so that
![]() $\unicode[STIX]{x1D6FC}_{i}=\unicode[STIX]{x1D6FD}_{i}p^{2n_{i}+1}$
, and the integers
$\unicode[STIX]{x1D6FC}_{i}=\unicode[STIX]{x1D6FD}_{i}p^{2n_{i}+1}$
, and the integers
![]() $\unicode[STIX]{x1D6FD}_{i}$
are not divisible by
$\unicode[STIX]{x1D6FD}_{i}$
are not divisible by
![]() $p$
. Assume moreover that the equation
$p$
. Assume moreover that the equation
![]() $\unicode[STIX]{x1D6FD}_{1}x^{2}+\unicode[STIX]{x1D6FD}_{2}y^{2}=0$
has no solutions modulo
$\unicode[STIX]{x1D6FD}_{1}x^{2}+\unicode[STIX]{x1D6FD}_{2}y^{2}=0$
has no solutions modulo
![]() $p$
. Let
$p$
. Let
![]() $v\in \unicode[STIX]{x1D6EC}\otimes \mathbb{Q}$
be such that the value of the quadratic form on
$v\in \unicode[STIX]{x1D6EC}\otimes \mathbb{Q}$
be such that the value of the quadratic form on
![]() $v$
is an integer. Then this integer is divisible by
$v$
is an integer. Then this integer is divisible by
![]() $p$
.
$p$
.
Proof. This is by a direct computation, which is especially straightforward when one works in
![]() $\mathbb{Q}_{p}$
instead of
$\mathbb{Q}_{p}$
instead of
![]() $\mathbb{Q}$
.◻
$\mathbb{Q}$
.◻
Proof of Theorem 3.4.
By Meyer’s theorem [Reference MeyerMey84],
![]() $L$
has an isotropic vector (that is, a vector
$L$
has an isotropic vector (that is, a vector
![]() $v$
with
$v$
with
![]() $q(v)=0$
). The isotropic quadric
$q(v)=0$
). The isotropic quadric
![]() $\{v\in L\mid q(v)=0\}$
has infinitely many points if it has one, and not all of them are proportional. Take two of such nonproportional points
$\{v\in L\mid q(v)=0\}$
has infinitely many points if it has one, and not all of them are proportional. Take two of such nonproportional points
![]() $v$
and
$v$
and
![]() $v^{\prime }$
, and let
$v^{\prime }$
, and let
![]() $v_{1}:=av+bv^{\prime }$
. Then
$v_{1}:=av+bv^{\prime }$
. Then
![]() $q(v_{1})=2abq(v,v^{\prime })$
. Next, consider the lattice
$q(v_{1})=2abq(v,v^{\prime })$
. Next, consider the lattice
![]() $\langle v,v^{\prime }\rangle ^{\bot }$
of signature
$\langle v,v^{\prime }\rangle ^{\bot }$
of signature
![]() $(r-1,s-1)$
(here
$(r-1,s-1)$
(here
![]() $(r,s)$
denotes the signature of
$(r,s)$
denotes the signature of
![]() $L$
). It is always possible to find a vector
$L$
). It is always possible to find a vector
![]() $w\in \langle v,v^{\prime }\rangle ^{\bot }$
such that
$w\in \langle v,v^{\prime }\rangle ^{\bot }$
such that
![]() $q(w)$
is divisible by an odd power of a suitable sufficiently large prime number
$q(w)$
is divisible by an odd power of a suitable sufficiently large prime number
![]() $p>N$
, but not by an even one (for instance, consider a rank-2 sublattice where the form
$p>N$
, but not by an even one (for instance, consider a rank-2 sublattice where the form
![]() $q$
is equivalent to
$q$
is equivalent to
![]() $x^{2}-dy^{2}$
over
$x^{2}-dy^{2}$
over
![]() $\mathbb{Q}$
and pick a sufficiently large
$\mathbb{Q}$
and pick a sufficiently large
![]() $p$
such that
$p$
such that
![]() $d$
is a square modulo
$d$
is a square modulo
![]() $p$
; then one can choose a suitable
$p$
; then one can choose a suitable
![]() $w$
in such a sublattice). Now choose the multipliers
$w$
in such a sublattice). Now choose the multipliers
![]() $a,b$
in such a way that the lattice
$a,b$
in such a way that the lattice
![]() $\unicode[STIX]{x1D6EC}:=\langle v_{1},w\rangle$
satisfies assumptions of Proposition 3.6 with this
$\unicode[STIX]{x1D6EC}:=\langle v_{1},w\rangle$
satisfies assumptions of Proposition 3.6 with this
![]() $p$
and has signature
$p$
and has signature
![]() $(1,1)$
.◻
$(1,1)$
.◻
3.3 Sublattices of large rank and existence of parabolic automorphisms
The purpose of this section is to construct, in
![]() $H^{2}(M,\mathbb{Z})$
, primitive sublattices of larger rank not representing small numbers (except possibly zero). We use Nikulin’s theorem on primitive embeddings into unimodular lattices. As
$H^{2}(M,\mathbb{Z})$
, primitive sublattices of larger rank not representing small numbers (except possibly zero). We use Nikulin’s theorem on primitive embeddings into unimodular lattices. As
![]() $H^{2}(M,\mathbb{Z})$
is not always unimodular, we have to provide a trick which allows a reduction to the unimodular case. The trick consists in remarking that we can embed
$H^{2}(M,\mathbb{Z})$
is not always unimodular, we have to provide a trick which allows a reduction to the unimodular case. The trick consists in remarking that we can embed
![]() $H^{2}(M,\mathbb{Z})$
into a lattice of rank
$H^{2}(M,\mathbb{Z})$
into a lattice of rank
![]() $b_{2}(M)+3$
which over
$b_{2}(M)+3$
which over
![]() $\mathbb{Q}$
is equivalent to a ‘standard’ lattice
$\mathbb{Q}$
is equivalent to a ‘standard’ lattice
![]() $L_{\text{st}}=\sum \pm z_{i}^{2}$
(Theorem 3.7). Then we take a suitable
$L_{\text{st}}=\sum \pm z_{i}^{2}$
(Theorem 3.7). Then we take a suitable
![]() $\unicode[STIX]{x1D6EC}$
not representing numbers of absolute value less than
$\unicode[STIX]{x1D6EC}$
not representing numbers of absolute value less than
![]() $N$
(except possibly zero) and embed it into
$N$
(except possibly zero) and embed it into
![]() $L_{\text{st}}$
using Nikulin’s results from [Reference NikulinNik80]. The intersection
$L_{\text{st}}$
using Nikulin’s results from [Reference NikulinNik80]. The intersection
![]() $\unicode[STIX]{x1D6EC}\,\cap \,H^{2}(M,\mathbb{Z})$
is not necessarily primitive in
$\unicode[STIX]{x1D6EC}\,\cap \,H^{2}(M,\mathbb{Z})$
is not necessarily primitive in
![]() $H^{2}(M,\mathbb{Z})$
, but we can control the extent to which it is not primitive in terms depending only on the embedding of
$H^{2}(M,\mathbb{Z})$
, but we can control the extent to which it is not primitive in terms depending only on the embedding of
![]() $H^{2}(M,\mathbb{Z})$
into
$H^{2}(M,\mathbb{Z})$
into
![]() $L_{\text{st}}$
, and not on
$L_{\text{st}}$
, and not on
![]() $N$
; so, increasing
$N$
; so, increasing
![]() $N$
if necessary, we eventually get a primitive sublattice satisfying the MBM bound.
$N$
if necessary, we eventually get a primitive sublattice satisfying the MBM bound.
For a lattice
![]() $\unicode[STIX]{x1D6EC}$
, we sometimes denote
$\unicode[STIX]{x1D6EC}$
, we sometimes denote
![]() $\unicode[STIX]{x1D6EC}\otimes _{\mathbb{Z}}\mathbb{Q}$
by
$\unicode[STIX]{x1D6EC}\otimes _{\mathbb{Z}}\mathbb{Q}$
by
![]() $\unicode[STIX]{x1D6EC}_{\mathbb{Q}}$
. Recall that the Hilbert symbol
$\unicode[STIX]{x1D6EC}_{\mathbb{Q}}$
. Recall that the Hilbert symbol
![]() $(a,b)_{p}$
of two
$(a,b)_{p}$
of two
![]() $p$
-adic numbers is equal to 1 if the equation
$p$
-adic numbers is equal to 1 if the equation
![]() $ax^{2}+by^{2}=z^{2}$
has nonzero solutions in
$ax^{2}+by^{2}=z^{2}$
has nonzero solutions in
![]() $\mathbb{Q}_{p}$
and
$\mathbb{Q}_{p}$
and
![]() $-1$
otherwise. If
$-1$
otherwise. If
![]() $a$
and
$a$
and
![]() $b$
are nonzero rational numbers, one has
$b$
are nonzero rational numbers, one has
![]() $(a,b)_{p}=1$
for all
$(a,b)_{p}=1$
for all
![]() $p$
except finitely many, and
$p$
except finitely many, and
![]() $\prod _{p}(a,b)_{p}=1$
[Reference SerreSer73, ch. III, Theorem 3]. Let
$\prod _{p}(a,b)_{p}=1$
[Reference SerreSer73, ch. III, Theorem 3]. Let
![]() $(V,q)$
be a rational quadratic space (that is, a rational vector space
$(V,q)$
be a rational quadratic space (that is, a rational vector space
![]() $V$
with a quadratic form
$V$
with a quadratic form
![]() $q$
,
$q$
,
![]() $\operatorname{Ker}(q)=\{0\}$
). The form
$\operatorname{Ker}(q)=\{0\}$
). The form
![]() $q$
diagonalizes in suitable coordinates; let
$q$
diagonalizes in suitable coordinates; let
![]() $a_{1},\ldots ,a_{n}$
be its diagonal entries and
$a_{1},\ldots ,a_{n}$
be its diagonal entries and
![]() $d=a_{1}\ldots a_{n}$
. It is well known that a nondegenerate rational quadratic form is determined by its signature, its discriminant
$d=a_{1}\ldots a_{n}$
. It is well known that a nondegenerate rational quadratic form is determined by its signature, its discriminant
![]() $d$
as an element of
$d$
as an element of
![]() $\mathbb{Q}^{\ast }/(\mathbb{Q}^{\ast })^{2}$
and its collection of
$\mathbb{Q}^{\ast }/(\mathbb{Q}^{\ast })^{2}$
and its collection of
![]() $p$
-adic signatures
$p$
-adic signatures
![]() $\unicode[STIX]{x1D700}_{p}(q)=\prod _{i<j}(a_{i},a_{j})_{p}$
for all primes
$\unicode[STIX]{x1D700}_{p}(q)=\prod _{i<j}(a_{i},a_{j})_{p}$
for all primes
![]() $p$
, where
$p$
, where
![]() $(a_{i},a_{j})_{p}$
is the Hilbert symbol [Reference SerreSer73, ch. IV.2, Theorems 9 and 7].
$(a_{i},a_{j})_{p}$
is the Hilbert symbol [Reference SerreSer73, ch. IV.2, Theorems 9 and 7].
As pointed out to us by the referee, the following statement is also well known.
Theorem 3.7. Let
![]() $(V,q_{V})$
and
$(V,q_{V})$
and
![]() $(W,q_{W})$
be rational nondegenerate quadratic spaces with
$(W,q_{W})$
be rational nondegenerate quadratic spaces with
![]() $\dim (V)>\dim (W)+2$
and signatures
$\dim (V)>\dim (W)+2$
and signatures
![]() $(r_{V},s_{V})$
,
$(r_{V},s_{V})$
,
![]() $(r_{W},s_{W})$
satisfying
$(r_{W},s_{W})$
satisfying
![]() $r_{W}\leqslant r_{V}$
,
$r_{W}\leqslant r_{V}$
,
![]() $s_{W}\leqslant s_{V}$
. Then there is an embedding of
$s_{W}\leqslant s_{V}$
. Then there is an embedding of
![]() $W$
into
$W$
into
![]() $V$
. In particular, for any nondegenerate lattice
$V$
. In particular, for any nondegenerate lattice
![]() $(H,q)$
, there is an embedding of rational quadratic spaces
$(H,q)$
, there is an embedding of rational quadratic spaces
![]() $(H\otimes _{\mathbb{Z}}\mathbb{Q},q)\subset (L_{\mathbb{Q}},q_{\text{st}})$
, where
$(H\otimes _{\mathbb{Z}}\mathbb{Q},q)\subset (L_{\mathbb{Q}},q_{\text{st}})$
, where
![]() $q_{\text{st}}=\sum \pm z_{i}^{2}$
, the rank of
$q_{\text{st}}=\sum \pm z_{i}^{2}$
, the rank of
![]() $L_{\mathbb{Q}}$
is equal to
$L_{\mathbb{Q}}$
is equal to
![]() $rk(H)+3$
and the signature of
$rk(H)+3$
and the signature of
![]() $L_{\mathbb{Q}}$
can be taken arbitrary among the possible ones
$L_{\mathbb{Q}}$
can be taken arbitrary among the possible ones
![]() $(r+3,s)$
;
$(r+3,s)$
;
![]() $(r+2,s+1)$
;
$(r+2,s+1)$
;
![]() $(r+1,s+2)$
;
$(r+1,s+2)$
;
![]() $(r,s+3)$
, where
$(r,s+3)$
, where
![]() $(r,s)$
is the signature of
$(r,s)$
is the signature of
![]() $H$
.
$H$
.
Proof. Since a rational quadratic space is determined by its invariants listed above, we just need to find a quadratic space
![]() $(U,q_{U})$
of dimension
$(U,q_{U})$
of dimension
![]() $\dim (V)-\dim (W)$
such that
$\dim (V)-\dim (W)$
such that
![]() $(U\oplus W,q_{U}\oplus q_{W})$
has the same invariants as
$(U\oplus W,q_{U}\oplus q_{W})$
has the same invariants as
![]() $(V,q_{V})$
. This is equivalent to finding a quadratic space with given invariants
$(V,q_{V})$
. This is equivalent to finding a quadratic space with given invariants
![]() $(r,s),d,\unicode[STIX]{x1D700}_{p}$
satisfying obvious compatibility conditions such as the product formula
$(r,s),d,\unicode[STIX]{x1D700}_{p}$
satisfying obvious compatibility conditions such as the product formula
![]() $\prod _{p}\unicode[STIX]{x1D700}_{p}=1$
. By [Reference SerreSer73, ch. IV.4, Proposition 7], this is always possible when
$\prod _{p}\unicode[STIX]{x1D700}_{p}=1$
. By [Reference SerreSer73, ch. IV.4, Proposition 7], this is always possible when
![]() $\dim (V)-\dim (W)\geqslant 3$
. The partial case in the theorem results by adjusting the signature of
$\dim (V)-\dim (W)\geqslant 3$
. The partial case in the theorem results by adjusting the signature of
![]() $q_{\text{st}}$
.◻
$q_{\text{st}}$
.◻
Let now
![]() $H$
be
$H$
be
![]() $H^{2}(M,\mathbb{Z})$
of signature
$H^{2}(M,\mathbb{Z})$
of signature
![]() $(3,b_{2}-3)$
,
$(3,b_{2}-3)$
,
![]() $L_{\mathbb{Q}}$
as in Theorem 3.7, say, of signature
$L_{\mathbb{Q}}$
as in Theorem 3.7, say, of signature
![]() $(3,b_{2})$
, and let
$(3,b_{2})$
, and let
![]() $L$
be the standard integral lattice in
$L$
be the standard integral lattice in
![]() $L_{\mathbb{Q}}$
. This is an odd unimodular lattice. The following lemma, essentially due to Nikulin [Reference NikulinNik80, § 1.16], implies that we can primitively embed into
$L_{\mathbb{Q}}$
. This is an odd unimodular lattice. The following lemma, essentially due to Nikulin [Reference NikulinNik80, § 1.16], implies that we can primitively embed into
![]() $L$
any lattice
$L$
any lattice
![]() $\unicode[STIX]{x1D6EC}$
of signature
$\unicode[STIX]{x1D6EC}$
of signature
![]() $(1,[b_{2}/2])$
, without 2-torsion in the discriminant and not representing numbers of small absolute value other than zero (examples of such lattices are easily obtained, say, by multiplying a unimodular lattice by a large prime).
$(1,[b_{2}/2])$
, without 2-torsion in the discriminant and not representing numbers of small absolute value other than zero (examples of such lattices are easily obtained, say, by multiplying a unimodular lattice by a large prime).
Lemma 3.8. Let
![]() $L$
be a unimodular lattice of signature
$L$
be a unimodular lattice of signature
![]() $(r,s)$
and
$(r,s)$
and
![]() $\unicode[STIX]{x1D6EC}$
a nondegenerate lattice of signature
$\unicode[STIX]{x1D6EC}$
a nondegenerate lattice of signature
![]() $(r^{\prime },s^{\prime })$
without
$(r^{\prime },s^{\prime })$
without
![]() $2$
-torsion in its discriminant group
$2$
-torsion in its discriminant group
![]() $\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}$
. Assume that
$\unicode[STIX]{x1D6EC}^{\vee }/\unicode[STIX]{x1D6EC}$
. Assume that
![]() $r\leqslant r^{\prime }$
,
$r\leqslant r^{\prime }$
,
![]() $s\leqslant s^{\prime }$
and
$s\leqslant s^{\prime }$
and
![]() $2\operatorname{rk}\unicode[STIX]{x1D6EC}<\operatorname{rk}L$
. Then
$2\operatorname{rk}\unicode[STIX]{x1D6EC}<\operatorname{rk}L$
. Then
![]() $\unicode[STIX]{x1D6EC}$
has a primitive embedding into
$\unicode[STIX]{x1D6EC}$
has a primitive embedding into
![]() $L$
.
$L$
.
Proof. Under the above conditions, Nikulin in [Reference NikulinNik80, Theorems 1.10.1, 1.16.5 and 1.16.7] showed the existence of a lattice
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
of signature
$\unicode[STIX]{x1D6EC}^{\prime }$
of signature
![]() $(r-r^{\prime },s-s^{\prime })$
and the discriminant form opposite to that of
$(r-r^{\prime },s-s^{\prime })$
and the discriminant form opposite to that of
![]() $\unicode[STIX]{x1D6EC}$
. The direct sum
$\unicode[STIX]{x1D6EC}$
. The direct sum
![]() $\unicode[STIX]{x1D6EC}\oplus \unicode[STIX]{x1D6EC}^{\prime }$
then has a unimodular overlattice corresponding to a maximal isotropic subgroup in the direct sum of the discriminant groups (see [Reference NikulinNik80, § 1.6.4], where this is explained in detail in the even case; the odd case is analogous).◻
$\unicode[STIX]{x1D6EC}\oplus \unicode[STIX]{x1D6EC}^{\prime }$
then has a unimodular overlattice corresponding to a maximal isotropic subgroup in the direct sum of the discriminant groups (see [Reference NikulinNik80, § 1.6.4], where this is explained in detail in the even case; the odd case is analogous).◻
For our purposes, we are looking for a primitive sublattice in a smaller lattice
![]() $H$
. The problem which remains to treat is that the intersection
$H$
. The problem which remains to treat is that the intersection
![]() $\unicode[STIX]{x1D6EC}\,\cap \,H$
(of signature
$\unicode[STIX]{x1D6EC}\,\cap \,H$
(of signature
![]() $(1,[b_{2}/2]-3)$
) is not necessarily a primitive sublattice of
$(1,[b_{2}/2]-3)$
) is not necessarily a primitive sublattice of
![]() $H$
. But its nonprimitivity can be controlled in terms of the embedding of
$H$
. But its nonprimitivity can be controlled in terms of the embedding of
![]() $H$
into
$H$
into
![]() $L_{\mathbb{Q}}$
and thus does not depend on
$L_{\mathbb{Q}}$
and thus does not depend on
![]() $\unicode[STIX]{x1D6EC}$
, which means that
$\unicode[STIX]{x1D6EC}$
, which means that
![]() $\unicode[STIX]{x1D6EC}$
can be chosen in such a way that its ‘primitivization’ in
$\unicode[STIX]{x1D6EC}$
can be chosen in such a way that its ‘primitivization’ in
![]() $L$
still does not represent small numbers. This is the main point of the proof of our final theorem below.
$L$
still does not represent small numbers. This is the main point of the proof of our final theorem below.
Theorem 3.9. Let
![]() $M$
be a hyperkähler manifold and
$M$
be a hyperkähler manifold and
![]() $N$
a natural number. Then
$N$
a natural number. Then
![]() $H:=H^{2}(M,\mathbb{Z})$
contains a primitive sublattice of signature
$H:=H^{2}(M,\mathbb{Z})$
contains a primitive sublattice of signature
![]() $(1,[b_{2}/2]-3)$
which does not represent nonzero numbers of absolute value smaller than
$(1,[b_{2}/2]-3)$
which does not represent nonzero numbers of absolute value smaller than
![]() $N$
. In particular, there is a deformation of
$N$
. In particular, there is a deformation of
![]() $M$
of Picard rank
$M$
of Picard rank
![]() $[b_{2}/2]-2$
which does not have any MBM classes.
$[b_{2}/2]-2$
which does not have any MBM classes.
Proof. Consider the embedding of
![]() $H$
into
$H$
into
![]() $L_{\mathbb{Q}}$
of dimension
$L_{\mathbb{Q}}$
of dimension
![]() $b_{2}+3$
and signature
$b_{2}+3$
and signature
![]() $(3,b_{2})$
as in Theorem 3.7. Set
$(3,b_{2})$
as in Theorem 3.7. Set
![]() $d=|H/H\,\cap \,L|$
. Then, for any primitive sublattice
$d=|H/H\,\cap \,L|$
. Then, for any primitive sublattice
![]() $\unicode[STIX]{x1D6EC}$
of
$\unicode[STIX]{x1D6EC}$
of
![]() $L$
, the group
$L$
, the group
![]() $(H\,\cap \,\unicode[STIX]{x1D6EC}_{\mathbb{Q}})/(H\,\cap \,L\,\cap \,\unicode[STIX]{x1D6EC}_{\mathbb{Q}})=(H\,\cap \,\unicode[STIX]{x1D6EC}_{\mathbb{Q}})/(H\,\cap \,\unicode[STIX]{x1D6EC})$
embeds into
$(H\,\cap \,\unicode[STIX]{x1D6EC}_{\mathbb{Q}})/(H\,\cap \,L\,\cap \,\unicode[STIX]{x1D6EC}_{\mathbb{Q}})=(H\,\cap \,\unicode[STIX]{x1D6EC}_{\mathbb{Q}})/(H\,\cap \,\unicode[STIX]{x1D6EC})$
embeds into
![]() $H/H\,\cap \,L$
and so has cardinality at most
$H/H\,\cap \,L$
and so has cardinality at most
![]() $d$
. By Lemma 3.8, if we take a lattice
$d$
. By Lemma 3.8, if we take a lattice
![]() $\unicode[STIX]{x1D6EC}$
of signature
$\unicode[STIX]{x1D6EC}$
of signature
![]() $(1,[b_{2}/2])$
, without 2-torsion in the discriminant and not representing any nonzero number of absolute value less than
$(1,[b_{2}/2])$
, without 2-torsion in the discriminant and not representing any nonzero number of absolute value less than
![]() $d^{2}N$
, it admits a primitive embedding to
$d^{2}N$
, it admits a primitive embedding to
![]() $L$
. Then the ‘primitivization’ of
$L$
. Then the ‘primitivization’ of
![]() $\unicode[STIX]{x1D6EC}\,\cap \,H$
(that is,
$\unicode[STIX]{x1D6EC}\,\cap \,H$
(that is,
![]() $H\,\cap \,\unicode[STIX]{x1D6EC}_{\mathbb{Q}}\subset H$
) is a lattice of signature
$H\,\cap \,\unicode[STIX]{x1D6EC}_{\mathbb{Q}}\subset H$
) is a lattice of signature
![]() $(1,[b_{2}/2]-3)$
not representing nonzero numbers of absolute value less than
$(1,[b_{2}/2]-3)$
not representing nonzero numbers of absolute value less than
![]() $N$
. Taking as
$N$
. Taking as
![]() $N$
the MBM bound for our manifold
$N$
the MBM bound for our manifold
![]() $M$
, we obtain deformations with relatively large Picard number and no MBM classes.◻
$M$
, we obtain deformations with relatively large Picard number and no MBM classes.◻
Corollary 3.10. Let
![]() $M$
be a hyperkähler manifold with
$M$
be a hyperkähler manifold with
![]() $b_{2}(M)\geqslant 14$
. Then
$b_{2}(M)\geqslant 14$
. Then
![]() $M$
has a deformation admitting a parabolic automorphism.
$M$
has a deformation admitting a parabolic automorphism.
Proof.
Step 1. Let
![]() $\unicode[STIX]{x1D6EC}=H_{I}^{1,1}(M,\mathbb{Z})$
be a primitive lattice of corank 2 and signature
$\unicode[STIX]{x1D6EC}=H_{I}^{1,1}(M,\mathbb{Z})$
be a primitive lattice of corank 2 and signature
![]() $(1,n)$
in
$(1,n)$
in
![]() $H^{2}(M,\mathbb{Z})$
satisfying the MBM bound. Then
$H^{2}(M,\mathbb{Z})$
satisfying the MBM bound. Then
![]() $\operatorname{Aut}(M,\unicode[STIX]{x1D6FA})$
has finite index in
$\operatorname{Aut}(M,\unicode[STIX]{x1D6FA})$
has finite index in
![]() $O(\unicode[STIX]{x1D6EC})$
. It suffices to show that the Lie group
$O(\unicode[STIX]{x1D6EC})$
. It suffices to show that the Lie group
![]() $O(\unicode[STIX]{x1D6EC}\otimes _{\mathbb{Z}}\mathbb{R})$
contains a rational unipotent subgroup
$O(\unicode[STIX]{x1D6EC}\otimes _{\mathbb{Z}}\mathbb{R})$
contains a rational unipotent subgroup
![]() $U$
. Indeed, then
$U$
. Indeed, then
![]() $U\,\cap \,\operatorname{Aut}(M,\unicode[STIX]{x1D6FA})$
is infinite by an application of a theorem by Borel and Harish-Chandra [Reference BorelBH62, Theorem 9.4], which affirms that the subgroup of integral points of an algebraic group over
$U\,\cap \,\operatorname{Aut}(M,\unicode[STIX]{x1D6FA})$
is infinite by an application of a theorem by Borel and Harish-Chandra [Reference BorelBH62, Theorem 9.4], which affirms that the subgroup of integral points of an algebraic group over
![]() $\mathbb{Q}$
without nontrivial rational characters has finite covolume. All elements of
$\mathbb{Q}$
without nontrivial rational characters has finite covolume. All elements of
![]() $U\,\cap \,\operatorname{Aut}(M,\unicode[STIX]{x1D6FA})$
are parabolic.
$U\,\cap \,\operatorname{Aut}(M,\unicode[STIX]{x1D6FA})$
are parabolic.
Step 2. Suppose that there exists a rational vector
![]() $v$
with
$v$
with
![]() $q(v,v)=0$
, and let
$q(v,v)=0$
, and let
![]() $P\subset O(\unicode[STIX]{x1D6EC}\otimes _{\mathbb{Z}}\mathbb{R})$
be the stabilizer of
$P\subset O(\unicode[STIX]{x1D6EC}\otimes _{\mathbb{Z}}\mathbb{R})$
be the stabilizer of
![]() $v$
. This subgroup is clearly rational and parabolic; its unipotent radical is the group
$v$
. This subgroup is clearly rational and parabolic; its unipotent radical is the group
![]() $U$
which we require.
$U$
which we require.
Step 3. Such a rational vector exists for any indefinite lattice of rank
![]() ${\geqslant}5$
by Meyer’s theorem [Reference MeyerMey84]; therefore, as soon as
${\geqslant}5$
by Meyer’s theorem [Reference MeyerMey84]; therefore, as soon as
![]() $[b_{2}(M)/2]-2\geqslant 5$
,
$[b_{2}(M)/2]-2\geqslant 5$
,
![]() $\unicode[STIX]{x1D6EC}$
has parabolic elements in its orthogonal group.◻
$\unicode[STIX]{x1D6EC}$
has parabolic elements in its orthogonal group.◻
Remark 3.11. V. Nikulin in a private conversation has suggested an alternative way to embed a given lattice
![]() $\unicode[STIX]{x1D6EC}$
into a nonunimodular lattice. His method does not make explicit appeal to quadratic forms over the rationals and gives a slightly better bound for ‘most’ possible
$\unicode[STIX]{x1D6EC}$
into a nonunimodular lattice. His method does not make explicit appeal to quadratic forms over the rationals and gives a slightly better bound for ‘most’ possible
![]() $H$
. Namely, if one replaces
$H$
. Namely, if one replaces
![]() $H$
by a maximal overlattice
$H$
by a maximal overlattice
![]() $L$
whose values are still integers, its discriminant form is very particular and it happens to be unique in its genus except for small ranks. Then one can split off from
$L$
whose values are still integers, its discriminant form is very particular and it happens to be unique in its genus except for small ranks. Then one can split off from
![]() $L$
a large-rank unimodular lattice by producing a small-rank lattice with the same discriminant form as that of
$L$
a large-rank unimodular lattice by producing a small-rank lattice with the same discriminant form as that of
![]() $L$
and embedding it into
$L$
and embedding it into
![]() $L$
; finally, one embeds
$L$
; finally, one embeds
![]() $\unicode[STIX]{x1D6EC}$
into that unimodular lattice.
$\unicode[STIX]{x1D6EC}$
into that unimodular lattice.
Acknowledgements
We are grateful to Noam Elkies, David Speyer and other participants of the Mathoverflow discussion [M15] for their interest and advice, to Marat Rovinsky for his help with some computations, to Slava Nikulin for patiently explaining certain points of his work and to the referee for pointing out simplifications of our arguments on quadratic forms.
Appendix A Cohomology vanishing
The hyperkähler manifolds without MBM classes have a cohomological property which can be worth mentioning. Namely, Verbitsky in [Reference VerbitskyVer07] has shown the following.
Theorem A.1 [Reference VerbitskyVer07, Theorem 5.6].
Let
![]() $M$
be an irreducible holomorphic symplectic manifold and
$M$
be an irreducible holomorphic symplectic manifold and
![]() $L$
a line bundle on
$L$
a line bundle on
![]() $M$
. Denote by
$M$
. Denote by
![]() $\overline{{\mathcal{K}}}\check{\;}\subset H^{1,1}(M)\,\cap \,H^{2}(M,\mathbb{R})$
the closure of the dual of the Kähler cone. Then:
$\overline{{\mathcal{K}}}\check{\;}\subset H^{1,1}(M)\,\cap \,H^{2}(M,\mathbb{R})$
the closure of the dual of the Kähler cone. Then:
-
(i) if
 $c_{1}(L)\in \overline{{\mathcal{K}}}\check{\;}$
, then
$c_{1}(L)\in \overline{{\mathcal{K}}}\check{\;}$
, then
 $H^{i}(L)=0$
for
$H^{i}(L)=0$
for
 $i>(\dim M)/2$
;
$i>(\dim M)/2$
; -
(ii) if
 $c_{1}(L)\in -\overline{{\mathcal{K}}}\check{\;}$
, then
$c_{1}(L)\in -\overline{{\mathcal{K}}}\check{\;}$
, then
 $H^{i}(L)=0$
for
$H^{i}(L)=0$
for
 $i<(\dim M)/2$
;
$i<(\dim M)/2$
; -
(iii) if
 $c_{1}(L)$
does not lie in
$c_{1}(L)$
does not lie in
 $-\overline{{\mathcal{K}}}\check{\;}\cup \overline{{\mathcal{K}}}\check{\;}$
, then
$-\overline{{\mathcal{K}}}\check{\;}\cup \overline{{\mathcal{K}}}\check{\;}$
, then
 $H^{i}(L)=0$
for
$H^{i}(L)=0$
for
 $i\neq (\dim M)/2$
.
$i\neq (\dim M)/2$
.
In our situation, the Kähler cone coincides with the positive cone and so the closure of its dual is just the closure of the positive cone. Together with the Kodaira vanishing, this yields the following result.
Corollary A.2. Let
![]() $M$
be an IHSM without MBM classes of type
$M$
be an IHSM without MBM classes of type
![]() $(1,1)$
(e.g. such that its Picard lattice does not represent small negative numbers), and
$(1,1)$
(e.g. such that its Picard lattice does not represent small negative numbers), and
![]() $L$
a line bundle on
$L$
a line bundle on
![]() $M$
with Beauville–Bogomolov square
$M$
with Beauville–Bogomolov square
![]() $q(L)\neq 0$
. Then
$q(L)\neq 0$
. Then
![]() $L$
can have nontrivial cohomologies in one degree only: degree zero if
$L$
can have nontrivial cohomologies in one degree only: degree zero if
![]() $c_{1}(L)$
is in the positive cone,
$c_{1}(L)$
is in the positive cone,
![]() $\dim M$
if
$\dim M$
if
![]() $-c_{1}(L)$
is in the positive cone and
$-c_{1}(L)$
is in the positive cone and
![]() $\dim M/2$
otherwise.
$\dim M/2$
otherwise.
See [Reference VerbitskyVer07] for similar results on cohomology, which become particularly simple in this context.