Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-26T04:58:01.529Z Has data issue: false hasContentIssue false
  • English
  • Français

Canonical bases arising from quantum symmetric pairs of Kac–Moody type

Part of: Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  22 June 2021

Huanchen Bao  and
Weiqiang Wang
Huanchen Bao
Affiliation:
Department of Mathematics, National University of Singapore, Republic of Singapore119076huanchen@nus.edu.sg
Weiqiang Wang
Affiliation:
Department of Mathematics, University of Virginia, Charlottesville, VA22904, USAww9c@virginia.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

For quantum symmetric pairs 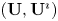$(\textbf {U}, \textbf {U}^\imath )$ of Kac–Moody type, we construct 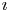$\imath$-canonical bases for the highest weight integrable $\textbf U$-modules and their tensor products regarded as 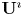$\textbf {U}^\imath$-modules, as well as an 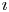$\imath$-canonical basis for the modified form of the 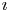$\imath$-quantum group 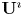$\textbf {U}^\imath$. A key new ingredient is a family of explicit elements called 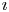$\imath$-divided powers, which are shown to generate the integral form of 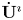$\dot {\textbf {U}}^\imath$. We prove a conjecture of Balagovic–Kolb, removing a major technical assumption in the theory of quantum symmetric pairs. Even for quantum symmetric pairs of finite type, our new approach simplifies and strengthens the integrality of quasi-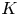$K$-matrix and the constructions of 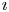$\imath$-canonical bases, by avoiding a case-by-case rank-one analysis and removing the strong constraints on the parameters in a previous work.

Keywords

quantum symmetric pairscanonical basesKac–Moody type

MSC classification

Primary: 17B10: Representations, algebraic theory (weights)
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 7 , July 2021 , pp. 1507 - 1537
Check for updates
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Araki, S., On root systems and an infinitesimal classification of irreducible symmetric spaces, J. Math. Osaka City Univ. 13 (1962), 1–34.Google Scholar
Balagovic, M. and Kolb, S., The bar involution for quantum symmetric pairs, Represent. Theory 19 (2015), 186–210.CrossRefGoogle Scholar
Balagovic, M. and Kolb, S., Universal $K$-matrix for quantum symmetric pairs, J. Reine Angew. Math. 747 (2019), 299–353.CrossRefGoogle Scholar
Bao, H., Kazhdan–Lusztig theory of super type $D$ and quantum symmetric pairs, Represent. Theory 21 (2017), 247–276.CrossRefGoogle Scholar
Bao, H., Kujawa, J., Li, Y. and Wang, W., Geometric Schur duality of classical type, [Appendix by Bao, Li and Wang], Transform. Groups 23 (2018), 329–389.CrossRefGoogle Scholar
Bao, H., Shan, P., Wang, W. and Webster, B., Categorification of quantum symmetric pairs I, Quantum Topol. 9 (2018), 643–714.CrossRefGoogle Scholar
Bao, H. and Wang, W., Canonical bases in tensor products revisited, Amer. J. Math. 138 (2016), 1731–1738.CrossRefGoogle Scholar
Bao, H. and Wang, W., A new approach to Kazhdan–Lusztig theory of type $B$ via quantum symmetric pairs, Astérisque 402 (2018), arXiv:1310.0103.Google Scholar
Bao, H. and Wang, W., Canonical bases arising from quantum symmetric pairs, Invent. Math. 213 (2018), 1099–1177.CrossRefGoogle Scholar
Bao, H., Wang, W. and Watanabe, H., Canonical bases for tensor products and super Kazhdan–Lusztig theory, J. Pure Appl. Algebra 224 (2020), 106347.CrossRefGoogle Scholar
Berman, C. and Wang, W., Formulae of $\imath$-divided powers in ${\bf U}_q(\mathfrak {sl}_2)$, J. Pure Appl. Algebra 222 (2018), 2667–2702; arXiv:1703.00602; II. arXiv:1806.00878.CrossRefGoogle Scholar
Chen, X., Lu, M. and Wang, W., A Serre presentation of $\imath$-quantum groups, Transform. Groups 2020, https://doi.org/10.1007/s00031-020-09581-5.CrossRefGoogle Scholar
Fan, Z., Lai, C., Li, Y., Luo, L. and Wang, W., Affine flag varieties and quantum symmetric pairs, Mem. Amer. Math. Soc. 265 (2020).Google Scholar
Joseph, A. and Letzter, G., Separation of variables for quantized enveloping algebras, Amer. J. Math. 116 (1994), 127–177.CrossRefGoogle Scholar
Joseph, A. and Letzter, G., Rosso's form and quantized Kac Moody algebras, Math. Z. 222 (1996), 543–571.CrossRefGoogle Scholar
Kashiwara, M., On crystal bases of the $Q$-analogue of universal enveloping algebras, Duke Math. J. 63 (1991), 456–516.CrossRefGoogle Scholar
Kashiwara, M., Crystal bases of modified quantized enveloping algebra, Duke Math. J. 73 (1994), 383–413.CrossRefGoogle Scholar
Kolb, S., Quantum symmetric Kac–Moody pairs, Adv. Math. 267 (2014), 395–469.CrossRefGoogle Scholar
Kolb, S., Braided module categories via quantum symmetric pairs, Proc. Lond. Math. Soc. (3) 121 (2020), 1–31.CrossRefGoogle Scholar
Letzter, G., Symmetric pairs for quantized enveloping algebras, J. Algebra 220 (1999), 729–767.CrossRefGoogle Scholar
Letzter, G., Coideal subalgebras and quantum symmetric pairs, New Directions in Hopf Algebras (Cambridge), MSRI Publications, vol. 43 (Cambridge University Press, 2002), 117–166.Google Scholar
Letzter, G., Quantum symmetric pairs and their zonal spherical functions, Transform. Groups 8 (2003), 261–292.CrossRefGoogle Scholar
Li, Y., Quiver varieties and symmetric pairs, Represent. Theory 23 (2019), 1–56.CrossRefGoogle Scholar
Li, Y. and Wang, W., Positivity vs negativity of canonical bases, Proceedings for Lusztig's 70th Birthday Conference, Bull. Inst. Math. Acad. Sin. (N.S.) 13 (2018), 143–198.Google Scholar
Lusztig, G., Canonical bases arising from quantized enveloping algebras, J. Amer. Math. Soc. 3 (1990), 447–498.CrossRefGoogle Scholar
Lusztig, G., Quivers, perverse sheaves, and quantized enveloping algebras, J. Amer. Math. Soc. 4 (1991), 365–421.CrossRefGoogle Scholar
Lusztig, G., Canonical bases in tensor products, Proc. Nat. Acad. Sci. 89 (1992), 8177–8179.CrossRefGoogle ScholarPubMed
Lusztig, G., Quantum groups at $v=\infty$, in Functional analysis on the eve of the 21st century, Progress in Mathematics, vol. 131 (Birkhauser, Boston, 1995), 199–221.CrossRefGoogle Scholar
Lusztig, G., Introduction to quantum groups, Modern Birkhäuser Classics, reprint of the 1993 edition (Birkhäuser, Boston, 2010).Google Scholar
Regelskis, V. and Vlaar, B., Reflection matrices, coideal subalgebras and generalized Satake diagrams of affine type, Preprint (2016), arXiv:1602.08471.Google Scholar