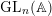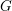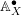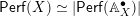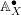Introduction
For a smooth, irreducible, complete, algebraic curve
![]() $X$
, we denote by
$X$
, we denote by
![]() $F$
the field of rational functions, by
$F$
the field of rational functions, by
![]() $\mathbb{O}$
the product
$\mathbb{O}$
the product
 $\prod _{x\in X_{\text{cl}}}\widehat{{\mathcal{O}}}_{x}$
ranging over closed points, and
$\prod _{x\in X_{\text{cl}}}\widehat{{\mathcal{O}}}_{x}$
ranging over closed points, and
 $$\begin{eqnarray}\mathbb{A}=\mathop{\prod }_{x\in X_{\text{cl}}}^{\!\!\!\prime }\,\widehat{F}_{x}=\{(f_{x})_{x\in X_{\text{cl}}}|f_{x}\in \widehat{{\mathcal{O}}}_{x}~\text{for almost all}~x\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{A}=\mathop{\prod }_{x\in X_{\text{cl}}}^{\!\!\!\prime }\,\widehat{F}_{x}=\{(f_{x})_{x\in X_{\text{cl}}}|f_{x}\in \widehat{{\mathcal{O}}}_{x}~\text{for almost all}~x\}.\end{eqnarray}$$
This object is called the ring of adèles. André Weil was probably the first to appreciate the close connection between adèles and the geometry of curves (see the letter [Reference WeilWei38b] to Hasse where the case of line bundles is discussed, and [Reference WeilWei38a] for the closely related notion of matrix divisors).
Theorem 0.1 (Weil).
Let
![]() $X$
be an algebraic curve, defined over an algebraically closed field
$X$
be an algebraic curve, defined over an algebraically closed field
![]() $k$
, and let
$k$
, and let
![]() $G$
be a reductive algebraic group. We then have an equivalence between the groupoid of
$G$
be a reductive algebraic group. We then have an equivalence between the groupoid of
![]() $G$
-torsors on
$G$
-torsors on
![]() $X$
,
$X$
,
![]() $BG(X)$
, and the groupoid defined by the double quotient
$BG(X)$
, and the groupoid defined by the double quotient
 $[G(F)\setminus G(\mathbb{A})/G(\mathbb{O})]$
.
$[G(F)\setminus G(\mathbb{A})/G(\mathbb{O})]$
.
Weil’s theorem is central to the geometric Langlands programme, as it connects the arithmetic conjectures to their geometric counterpart. For a survey of this connection see [Reference FrenkelFre07]. The interplay of Weil’s result with conformal field theory is discussed by Witten [Reference WittenWit88, § V].
In this article we present a generalisation of Weil’s theorem to arbitrary Noetherian schemes. We will deduce it from an adelic descent result for the perfect complexes. The co-simplicial ring
![]() $\mathbb{A}_{X}^{\bullet }$
was introduced by Beilinson in [Reference BeilinsonBei80], as a generalisation of the theory of adèles for curves. A similar construction has also been obtained by Parshin for algebraic surfaces. If
$\mathbb{A}_{X}^{\bullet }$
was introduced by Beilinson in [Reference BeilinsonBei80], as a generalisation of the theory of adèles for curves. A similar construction has also been obtained by Parshin for algebraic surfaces. If
![]() $X$
is a curve, the co-simplicial ring is given by the diagram
$X$
is a curve, the co-simplicial ring is given by the diagram

which captures the adelic rings
![]() $F$
,
$F$
,
![]() $\mathbb{O}_{X}$
and
$\mathbb{O}_{X}$
and
![]() $\mathbb{A}_{X}$
, and the various maps between them, used to formulate Weil’s Theorem 0.1.
$\mathbb{A}_{X}$
, and the various maps between them, used to formulate Weil’s Theorem 0.1.
Theorem 0.2 (Adelic descent).
Let
![]() $X$
be a Noetherian scheme. We denote by
$X$
be a Noetherian scheme. We denote by
![]() $\mathbb{A}_{X}^{\bullet }$
Beilinson’s co-simplicial ring of adèles (see Definition 1.4). We have an equivalence of symmetric monoidal
$\mathbb{A}_{X}^{\bullet }$
Beilinson’s co-simplicial ring of adèles (see Definition 1.4). We have an equivalence of symmetric monoidal
![]() $\infty$
-categories
$\infty$
-categories
 $\mathsf{Perf}(X)_{\otimes }\simeq |\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })_{\otimes }|$
, where the right-hand side denotes the
$\mathsf{Perf}(X)_{\otimes }\simeq |\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })_{\otimes }|$
, where the right-hand side denotes the
![]() $\infty$
-category of cartesian
$\infty$
-category of cartesian
![]() $\mathbb{A}_{X}^{\bullet }$
-modules.
$\mathbb{A}_{X}^{\bullet }$
-modules.
This theorem also holds for almost perfect complexes, as we show in Corollary 3.39. According to Lieblich, the study of perfect complexes is the mother of all moduli problems (see the abstract of [Reference LieblichLie06]). The Tannakian formalism enables us to make this philosophical principle precise. Using the results of Bhatt [Reference BhattBha16] and Bhatt and Halpern-Leistner [Reference Bhatt and Halpern-LeistnerBHL15], we obtain a descent result for
![]() $G$
-torsors (we may replace
$G$
-torsors (we may replace
![]() $BG$
by more general algebraic stacks).
$BG$
by more general algebraic stacks).
Theorem 0.3. Let
![]() $X$
be a Noetherian scheme. The geometric realisation of the simplicial affine scheme
$X$
be a Noetherian scheme. The geometric realisation of the simplicial affine scheme
 $\operatorname{Spec}\mathbb{A}_{X}^{\bullet }$
in the category of Noetherian algebraic stacks with quasi-affine diagonal is canonically equivalent to
$\operatorname{Spec}\mathbb{A}_{X}^{\bullet }$
in the category of Noetherian algebraic stacks with quasi-affine diagonal is canonically equivalent to
![]() $X$
. In particular, we have
$X$
. In particular, we have
 $BG(X)\simeq |BG(\operatorname{Spec}\mathbb{A}_{X}^{\bullet })|$
, if
$BG(X)\simeq |BG(\operatorname{Spec}\mathbb{A}_{X}^{\bullet })|$
, if
![]() $G$
is a Noetherian affine algebraic group scheme. Let
$G$
is a Noetherian affine algebraic group scheme. Let
![]() $G$
be a special group scheme (for example,
$G$
be a special group scheme (for example,
 $G=\operatorname{GL}_{n}$
). We denote by
$G=\operatorname{GL}_{n}$
). We denote by
 $G(\mathbb{A}_{X}^{1})^{\text{cocycle}}$
the subset consisting of
$G(\mathbb{A}_{X}^{1})^{\text{cocycle}}$
the subset consisting of
 $\unicode[STIX]{x1D719}\in \mathbb{G}(\mathbb{A}_{X}^{1})$
satisfying the cocycle condition
$\unicode[STIX]{x1D719}\in \mathbb{G}(\mathbb{A}_{X}^{1})$
satisfying the cocycle condition
 $\unicode[STIX]{x1D719}_{02}=\unicode[STIX]{x1D719}_{01}\circ \unicode[STIX]{x1D719}_{12}$
in
$\unicode[STIX]{x1D719}_{02}=\unicode[STIX]{x1D719}_{01}\circ \unicode[STIX]{x1D719}_{12}$
in
![]() $G(\mathbb{A}_{X}^{2})$
. There is an equivalence of groupoids
$G(\mathbb{A}_{X}^{2})$
. There is an equivalence of groupoids
 $BG(X)\simeq [G(\mathbb{A}_{X}^{1})^{\text{cocycle}}/G(\mathbb{A}_{X}^{0})]$
.
$BG(X)\simeq [G(\mathbb{A}_{X}^{1})^{\text{cocycle}}/G(\mathbb{A}_{X}^{0})]$
.
In characteristic 0, the assumption that
![]() $G$
be Noetherian can often be dropped. We refer the reader to Corollary 3.35. We refer the reader to § 3.2.4 for a more detailed discussion of the adelic description of
$G$
be Noetherian can often be dropped. We refer the reader to Corollary 3.35. We refer the reader to § 3.2.4 for a more detailed discussion of the adelic description of
![]() $G$
-bundles on Noetherian schemes
$G$
-bundles on Noetherian schemes
![]() $X$
. The case of punctured surfaces has also been considered by Garland and Patnaik in [Reference Garland and PatnaikGP]. In [Reference ParshinPar83], Parshin used adelic cocycles for
$X$
. The case of punctured surfaces has also been considered by Garland and Patnaik in [Reference Garland and PatnaikGP]. In [Reference ParshinPar83], Parshin used adelic cocycles for
![]() $G$
-bundles as above to obtain formulae for Chern classes in adelic terms.
$G$
-bundles as above to obtain formulae for Chern classes in adelic terms.
As a further consequence of the adelic descent formalism, we obtain an analogue of Gelfand–Naimark’s reconstruction theorem for locally compact topological spaces [Reference Gelfand and NaimarkGN43]. Recall that [Reference Gelfand and NaimarkGN43] shows that a locally compact topological space can be reconstructed from the ring of continuous functions. It is well-known that a similar result cannot hold for non-affine schemes. However, our result implies that a Noetherian scheme
![]() $X$
can be reconstructed from the co-simplicial ring of adèles.
$X$
can be reconstructed from the co-simplicial ring of adèles.
Theorem 0.4. The functor
 $\mathbb{A}^{\bullet }:\mathsf{Sch}^{N}{\hookrightarrow}(\mathsf{Rng}^{\unicode[STIX]{x1D6E5}})^{\mathsf{op}}$
from the category of Noetherian schemes to the dual category of co-simplicial commutative rings, has an explicit left-inverse, sending
$\mathbb{A}^{\bullet }:\mathsf{Sch}^{N}{\hookrightarrow}(\mathsf{Rng}^{\unicode[STIX]{x1D6E5}})^{\mathsf{op}}$
from the category of Noetherian schemes to the dual category of co-simplicial commutative rings, has an explicit left-inverse, sending
![]() $R^{\bullet }$
to
$R^{\bullet }$
to
 $|\operatorname{Spec}\,R^{\bullet }|$
.
$|\operatorname{Spec}\,R^{\bullet }|$
.
It is instructive to meditate on the differences and similarities with Gelfand–Naimark’s theorem. While their result copes with plain rings, our Theorem 0.4 requires a diagram of rings (see Corollary 3.33 for a precise statement to which extent the co-simplicial structure is needed). However, the necessary condition of local compactness for topological spaces is not unlike the restriction that the scheme be Noetherian.
For a quasi-compact and quasi-separated scheme
![]() $X$
we may choose a finite cover by affine open subschemes
$X$
we may choose a finite cover by affine open subschemes
 $\{U_{i}\}_{i=1,\ldots ,n}$
. The coproduct
$\{U_{i}\}_{i=1,\ldots ,n}$
. The coproduct
 $U=\coprod _{i=1}^{n}U_{i}$
is then still an affine scheme, and we have a map
$U=\coprod _{i=1}^{n}U_{i}$
is then still an affine scheme, and we have a map
![]() $U\rightarrow X$
. Choosing a finite affine covering for
$U\rightarrow X$
. Choosing a finite affine covering for
 $U\times _{X}U$
, and iterating this procedure, we arrive at a simplicial affine scheme
$U\times _{X}U$
, and iterating this procedure, we arrive at a simplicial affine scheme
 $U_{\bullet }\rightarrow X$
, which yields a hypercovering of
$U_{\bullet }\rightarrow X$
, which yields a hypercovering of
![]() $X$
. The coordinate ring yields a co-simplicial ring
$X$
. The coordinate ring yields a co-simplicial ring
![]() $\unicode[STIX]{x1D6E4}(U_{\bullet })$
associated to
$\unicode[STIX]{x1D6E4}(U_{\bullet })$
associated to
![]() $X$
. However, this construction is a priori not functorial, since it depends on the chosen coverings. Nonetheless, using the construction
$X$
. However, this construction is a priori not functorial, since it depends on the chosen coverings. Nonetheless, using the construction
 $X\mapsto X^{Z}$
introduced by Bhatt and Scholze [Reference Bhatt and ScholzeBS15], one obtains another functor as in Theorem 0.4 (the author thanks Bhatt for bringing this to his attention).
$X\mapsto X^{Z}$
introduced by Bhatt and Scholze [Reference Bhatt and ScholzeBS15], one obtains another functor as in Theorem 0.4 (the author thanks Bhatt for bringing this to his attention).
Our Theorem 0.2 relies heavily on Beilinson’s [Reference BeilinsonBei80], which constructs a functor, sending a quasi-coherent sheaf
![]() ${\mathcal{F}}$
on
${\mathcal{F}}$
on
![]() $X$
to an
$X$
to an
![]() $\mathbb{A}_{X}^{\bullet }$
-module
$\mathbb{A}_{X}^{\bullet }$
-module
![]() $\mathbb{A}_{X}^{\bullet }({\mathcal{F}})$
. Beilinson observes that the latter co-simplicial module gives rise to a chain complex, computing the cohomology of
$\mathbb{A}_{X}^{\bullet }({\mathcal{F}})$
. Beilinson observes that the latter co-simplicial module gives rise to a chain complex, computing the cohomology of
![]() ${\mathcal{F}}$
. This chain complex can be obtained by applying the Dold–Kan correspondence, or taking the alternating sum of the face maps in each degree:
${\mathcal{F}}$
. This chain complex can be obtained by applying the Dold–Kan correspondence, or taking the alternating sum of the face maps in each degree:
 $[\mathbb{A}^{0}({\mathcal{F}})\xrightarrow[{}]{\unicode[STIX]{x2202}_{0}-\unicode[STIX]{x2202}_{1}}\mathbb{A}^{1}({\mathcal{F}})\cdots \,]$
. Beilinson’s result can be stated as
$[\mathbb{A}^{0}({\mathcal{F}})\xrightarrow[{}]{\unicode[STIX]{x2202}_{0}-\unicode[STIX]{x2202}_{1}}\mathbb{A}^{1}({\mathcal{F}})\cdots \,]$
. Beilinson’s result can be stated as
 $$\begin{eqnarray}H^{i}(X,{\mathcal{F}})\simeq H^{i}(\mathsf{DK}(\mathbb{A}_{X}^{\bullet }({\mathcal{F}}))).\end{eqnarray}$$
$$\begin{eqnarray}H^{i}(X,{\mathcal{F}})\simeq H^{i}(\mathsf{DK}(\mathbb{A}_{X}^{\bullet }({\mathcal{F}}))).\end{eqnarray}$$
The reason is that the sheaves
 $\mathsf{A}_{X}^{k}:U\mapsto \mathbb{A}_{U}^{k}({\mathcal{F}})$
are flasque, and hence it remains to show that the corresponding complex of sheaves defines a flasque resolution of
$\mathsf{A}_{X}^{k}:U\mapsto \mathbb{A}_{U}^{k}({\mathcal{F}})$
are flasque, and hence it remains to show that the corresponding complex of sheaves defines a flasque resolution of
![]() ${\mathcal{F}}$
. The details are explained in [Reference HuberHub91]. Since morphisms in
${\mathcal{F}}$
. The details are explained in [Reference HuberHub91]. Since morphisms in
 $\mathsf{Perf}(X)$
are closely related to sheaf cohomology, it is not difficult to deduce from Beilinson’s observation the existence of a fully faithful functor
$\mathsf{Perf}(X)$
are closely related to sheaf cohomology, it is not difficult to deduce from Beilinson’s observation the existence of a fully faithful functor
 $\mathsf{Perf}(X){\hookrightarrow}|\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })|$
, amounting to a sort of a cohomological descent result. Our proof of the adelic descent theorem is, hence, mainly concerned with establishing that this functor is essentially surjective, that is, establishing effectivity of descent for objects in those
$\mathsf{Perf}(X){\hookrightarrow}|\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })|$
, amounting to a sort of a cohomological descent result. Our proof of the adelic descent theorem is, hence, mainly concerned with establishing that this functor is essentially surjective, that is, establishing effectivity of descent for objects in those
![]() $\infty$
-categories. In heuristic terms, our theorem asserts that a perfect complex
$\infty$
-categories. In heuristic terms, our theorem asserts that a perfect complex
![]() $M$
on
$M$
on
![]() $X$
can be described by an iterative formal glueing procedure from the adelic parts
$X$
can be described by an iterative formal glueing procedure from the adelic parts
![]() $\mathbb{A}_{X}^{\bullet }(M)$
.
$\mathbb{A}_{X}^{\bullet }(M)$
.
Our main theorem uses the language of stable
![]() $\infty$
-categories. Replacing
$\infty$
-categories. Replacing
 $\mathsf{Perf}(X)$
and
$\mathsf{Perf}(X)$
and
 $\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })$
by their homotopy categories would render the result incorrect. However, the theorem could be formulated in more classical language. The
$\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })$
by their homotopy categories would render the result incorrect. However, the theorem could be formulated in more classical language. The
![]() $\infty$
-category of cartesian perfect modules over a co-simplicial ring, such as
$\infty$
-category of cartesian perfect modules over a co-simplicial ring, such as
 $\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })$
, has a model, as is discussed in [Reference Toën and VezzosiTV08, 1.2.12] by Toën and Vezzosi.
$\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })$
, has a model, as is discussed in [Reference Toën and VezzosiTV08, 1.2.12] by Toën and Vezzosi.
Since the construction of
![]() $\mathbb{A}_{X}^{\bullet }$
involves iterative completion and localisation procedures, the formal descent result of Beauville and Laszlo [Reference Beauville and LaszloBL95] and Ben-Bassat and Temkin [Reference Ben-Bassat and TemkinBBT13] (for quasi-coherent sheaves in each case) are closely related. These theorems allow one to glue sheaves on a scheme
$\mathbb{A}_{X}^{\bullet }$
involves iterative completion and localisation procedures, the formal descent result of Beauville and Laszlo [Reference Beauville and LaszloBL95] and Ben-Bassat and Temkin [Reference Ben-Bassat and TemkinBBT13] (for quasi-coherent sheaves in each case) are closely related. These theorems allow one to glue sheaves on a scheme
![]() $X$
with respect to the formal neighbourhood of a closed subvariety
$X$
with respect to the formal neighbourhood of a closed subvariety
![]() $Y$
, and its open complement
$Y$
, and its open complement
![]() $X\setminus Y$
. Beauville–Laszlo developed such a descent theory for an affine scheme
$X\setminus Y$
. Beauville–Laszlo developed such a descent theory for an affine scheme
![]() $X$
, and a closed subvariety
$X$
, and a closed subvariety
![]() $Y$
given by a principal ideal. This result was motivated by the study of conformal blocks [Reference Beauville and LaszloBL94]. The second article does not require the restrictions of
$Y$
given by a principal ideal. This result was motivated by the study of conformal blocks [Reference Beauville and LaszloBL94]. The second article does not require the restrictions of
![]() $X$
to be affine and
$X$
to be affine and
![]() $Y$
to be principal, however it utilises the theory of Berkovich spaces to formulate the glueing result. Recently their theory has been extended to treat flags of subvarieties by Hennion, Porta and Vezzosi [Reference Hennion, Porta and VezzosiHPV16]. Our Theorem 0.2 gives a very similar descent theory, but uses all closed subvarieties at once and avoids rigid geometry.
$Y$
to be principal, however it utilises the theory of Berkovich spaces to formulate the glueing result. Recently their theory has been extended to treat flags of subvarieties by Hennion, Porta and Vezzosi [Reference Hennion, Porta and VezzosiHPV16]. Our Theorem 0.2 gives a very similar descent theory, but uses all closed subvarieties at once and avoids rigid geometry.
One of the key properties of the adèles allowing one to establish effectivity of adelic descent data is a strengthening of the theory of flasque sheaves of algebras.
Theorem 0.5. Let
![]() $X$
be a quasi-compact topological space and
$X$
be a quasi-compact topological space and
![]() $\mathsf{A}$
a lâche sheaf of algebras (see Definition 2.9), with ring of global sections
$\mathsf{A}$
a lâche sheaf of algebras (see Definition 2.9), with ring of global sections
 $R=\unicode[STIX]{x1D6E4}(\mathsf{A})$
. The global section functor
$R=\unicode[STIX]{x1D6E4}(\mathsf{A})$
. The global section functor
 $\unicode[STIX]{x1D6E4}:\mathsf{Mod}(\mathsf{A})\rightarrow \mathsf{Mod}(\mathsf{A})$
restricts to a symmetric monoidal equivalence
$\unicode[STIX]{x1D6E4}:\mathsf{Mod}(\mathsf{A})\rightarrow \mathsf{Mod}(\mathsf{A})$
restricts to a symmetric monoidal equivalence
 $\mathsf{Perf}(\mathsf{A})_{\otimes }\simeq \mathsf{Perf}(R)_{\otimes }$
.
$\mathsf{Perf}(\mathsf{A})_{\otimes }\simeq \mathsf{Perf}(R)_{\otimes }$
.
We show in Lemma 1.14 that the adèles
![]() $\mathbb{A}_{X}^{k}$
are lâche sheaves of algebras. The derived equivalence underlying our theorems decomposes into two parts:
$\mathbb{A}_{X}^{k}$
are lâche sheaves of algebras. The derived equivalence underlying our theorems decomposes into two parts:
 $$\begin{eqnarray}\mathsf{Perf}(X)\simeq |\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|\simeq |\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })|.\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Perf}(X)\simeq |\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|\simeq |\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })|.\end{eqnarray}$$
The second equivalence is deduced from Theorem 0.5. The first equivalence can be established by local verifications.
1 A reminder of Beilinson–Parshin adèles
In [Reference BeilinsonBei80] Beilinson generalised the notion of adèles to arbitrary Noetherian schemes, and studied the connection adèles bear with coherent cohomology. We briefly review his definition and the main properties of relevance to us. Except for the assertion that adèles are flasque sheaves (Corollary 1.15), we will not provide a proof for those statements and refer the reader instead to Huber [Reference HuberHub91]. Examples can be found in Morrow’s survey article about adèles and their relation to higher local fields [Reference MorrowMor12].
1.1 Recollection
Henceforth we denote by
![]() $X$
a Noetherian scheme, with underlying topological space
$X$
a Noetherian scheme, with underlying topological space
![]() $|X|$
and structure sheaf
$|X|$
and structure sheaf
![]() ${\mathcal{O}}_{X}$
.
${\mathcal{O}}_{X}$
.
Definition 1.1. Let
![]() $X$
be a scheme with underlying topological space
$X$
be a scheme with underlying topological space
![]() $|X|$
. For
$|X|$
. For
 $x,y\in |X|$
we write
$x,y\in |X|$
we write
![]() $x\leqslant y$
for
$x\leqslant y$
for
 $x\in \overline{\{y\}}$
; this defines a partially ordered set
$x\in \overline{\{y\}}$
; this defines a partially ordered set
![]() $|X|_{{\leqslant}}$
. We denote the set
$|X|_{{\leqslant}}$
. We denote the set
 $\{(x_{0},\ldots ,x_{k})\in |X|^{\times k+1}|x_{0}\leqslant \cdots \leqslant x_{k}\}$
by
$\{(x_{0},\ldots ,x_{k})\in |X|^{\times k+1}|x_{0}\leqslant \cdots \leqslant x_{k}\}$
by
![]() $|X|_{k}$
.
$|X|_{k}$
.
One sees that
![]() $|X|_{k}$
is in fact the set of
$|X|_{k}$
is in fact the set of
![]() $k$
-simplices of a simplicial set
$k$
-simplices of a simplicial set
![]() $|X|_{\bullet }$
. This simplicial structure will be reflected in a co-simplicial structure for Beilinson–Parshin adèles.
$|X|_{\bullet }$
. This simplicial structure will be reflected in a co-simplicial structure for Beilinson–Parshin adèles.
Definition 1.2. The simplicial set
 $|X|_{\bullet }:\unicode[STIX]{x1D6E5}^{\mathsf{op}}\rightarrow \operatorname{Set}$
is defined to be the functor, sending
$|X|_{\bullet }:\unicode[STIX]{x1D6E5}^{\mathsf{op}}\rightarrow \operatorname{Set}$
is defined to be the functor, sending
 $[n]\in \unicode[STIX]{x1D6E5}^{\mathsf{op}}$
to the set of ordered maps
$[n]\in \unicode[STIX]{x1D6E5}^{\mathsf{op}}$
to the set of ordered maps
 $[n]\rightarrow |X|_{{\leqslant}}$
, where
$[n]\rightarrow |X|_{{\leqslant}}$
, where
![]() $|X|_{{\leqslant}}$
refers to the partially ordered set defined in Definition 1.1.
$|X|_{{\leqslant}}$
refers to the partially ordered set defined in Definition 1.1.
Following [Reference BeilinsonBei80] we define adèles with respect to a subset
 $T\subset |X|_{k}$
. The case of interest to us will be
$T\subset |X|_{k}$
. The case of interest to us will be
 $T=|X|_{k}$
, but the recursive nature of the definition necessitates a definition for general subsets
$T=|X|_{k}$
, but the recursive nature of the definition necessitates a definition for general subsets
 $T\subset |X|_{k}$
. We begin with the following preliminary definitions.
$T\subset |X|_{k}$
. We begin with the following preliminary definitions.
Definition 1.3. Let
![]() $X$
be a Noetherian scheme and
$X$
be a Noetherian scheme and
![]() $k\in \mathbb{N}$
a non-negative integer:
$k\in \mathbb{N}$
a non-negative integer:
-
(a) for
 $x\in |X|$
and
$x\in |X|$
and
 $T\subset |X|_{k}$
we define
$T\subset |X|_{k}$
we define
 $\text{}_{x}T=\{(x_{0}\leqslant \cdots \leqslant x_{k-1})\in |X|^{\times k}|(x_{0}\leqslant \cdots \leqslant x_{k-1}\leqslant x)\in T\}$
;
$\text{}_{x}T=\{(x_{0}\leqslant \cdots \leqslant x_{k-1})\in |X|^{\times k}|(x_{0}\leqslant \cdots \leqslant x_{k-1}\leqslant x)\in T\}$
; -
(b) for
 $x\in |X|$
we denote by
$x\in |X|$
we denote by
 ${\mathcal{O}}_{x}$
the local ring at
${\mathcal{O}}_{x}$
the local ring at
 $x$
with maximal ideal
$x$
with maximal ideal
 $\mathfrak{m}_{x}$
; there is a canonical morphism
$\mathfrak{m}_{x}$
; there is a canonical morphism
 $j_{rx}:\operatorname{Spec}{\mathcal{O}}_{x}/\mathfrak{m}_{x}^{r}\rightarrow X$
.
$j_{rx}:\operatorname{Spec}{\mathcal{O}}_{x}/\mathfrak{m}_{x}^{r}\rightarrow X$
.
It is convenient to define adèles in a higher-dimensional situation as sheaves of
![]() ${\mathcal{O}}_{X}$
-modules.
${\mathcal{O}}_{X}$
-modules.
Definition 1.4. Let
![]() $X$
be a Noetherian scheme. The adèles are the unique family of exact functors
$X$
be a Noetherian scheme. The adèles are the unique family of exact functors
 $\mathsf{A}_{X,T}(-):\mathsf{QCoh}(X)\rightarrow \mathsf{Mod}({\mathcal{O}}_{X})$
, indexed by subsets
$\mathsf{A}_{X,T}(-):\mathsf{QCoh}(X)\rightarrow \mathsf{Mod}({\mathcal{O}}_{X})$
, indexed by subsets
 $T\subset |X|_{k}$
, satisfying the following conditions:
$T\subset |X|_{k}$
, satisfying the following conditions:
-
(a) the functor
 $\mathsf{A}_{X,T}(-)$
commutes with directed colimits;
$\mathsf{A}_{X,T}(-)$
commutes with directed colimits; -
(b) for
 ${\mathcal{F}}\in \mathsf{Coh}(X)$
and
${\mathcal{F}}\in \mathsf{Coh}(X)$
and
 $k=0$
we have
$k=0$
we have
 $\mathsf{A}_{X,T}({\mathcal{F}})=\prod _{x\in T}\mathop{\varprojlim }\nolimits_{r\geqslant 0}(j_{rx})_{\ast }(j_{rx})^{\ast }{\mathcal{F}}$
;
$\mathsf{A}_{X,T}({\mathcal{F}})=\prod _{x\in T}\mathop{\varprojlim }\nolimits_{r\geqslant 0}(j_{rx})_{\ast }(j_{rx})^{\ast }{\mathcal{F}}$
; -
(c) for
 ${\mathcal{F}}\in \mathsf{Coh}(X)$
and
${\mathcal{F}}\in \mathsf{Coh}(X)$
and
 $k\geqslant 1$
we have
$k\geqslant 1$
we have
 $\mathsf{A}_{X,T}({\mathcal{F}})=\prod _{x\in |X|}\mathop{\varprojlim }\nolimits_{r\geqslant 0}\mathsf{A}_{X,\text{}_{x}T}((j_{rx})_{\ast }(j_{rx})^{\ast }{\mathcal{F}})$
.
$\mathsf{A}_{X,T}({\mathcal{F}})=\prod _{x\in |X|}\mathop{\varprojlim }\nolimits_{r\geqslant 0}\mathsf{A}_{X,\text{}_{x}T}((j_{rx})_{\ast }(j_{rx})^{\ast }{\mathcal{F}})$
.
We refer the reader to [Reference HuberHub91] for a detailed verification that the above family of functors is well-defined and exact. The ring of adéles with respect to
 $T\subset |X|_{n}$
is defined by taking global sections of the sheaf of rings
$T\subset |X|_{n}$
is defined by taking global sections of the sheaf of rings
 $\mathsf{A}_{X,T}({\mathcal{O}}_{X})$
. Moreover, it is important to emphasise that the sheaves of
$\mathsf{A}_{X,T}({\mathcal{O}}_{X})$
. Moreover, it is important to emphasise that the sheaves of
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
 $\mathsf{A}_{X,T}({\mathcal{F}})$
are in general not quasi-coherent.
$\mathsf{A}_{X,T}({\mathcal{F}})$
are in general not quasi-coherent.
Definition 1.5. We denote the abelian group
 $\unicode[STIX]{x1D6E4}(X,\mathsf{A}_{X,T}({\mathcal{F}}))$
by
$\unicode[STIX]{x1D6E4}(X,\mathsf{A}_{X,T}({\mathcal{F}}))$
by
 $\mathbb{A}_{X,T}({\mathcal{F}})$
; and reserve the notation
$\mathbb{A}_{X,T}({\mathcal{F}})$
; and reserve the notation
![]() $\mathbb{A}_{X,T}$
for
$\mathbb{A}_{X,T}$
for
 $\mathbb{A}_{X,T}({\mathcal{O}}_{X})$
. By construction
$\mathbb{A}_{X,T}({\mathcal{O}}_{X})$
. By construction
 $\mathbb{A}_{X,T}({\mathcal{F}})$
is an
$\mathbb{A}_{X,T}({\mathcal{F}})$
is an
![]() $\mathbb{A}_{X,T}$
-module.
$\mathbb{A}_{X,T}$
-module.
As we already alluded to, the most interesting case for us is when
 $T=|X|_{k}$
. We reserve a particular notation for this situation.
$T=|X|_{k}$
. We reserve a particular notation for this situation.
Definition 1.6. We denote the sheaf
 $\mathsf{A}_{X,|X|_{k}}({\mathcal{F}})$
by
$\mathsf{A}_{X,|X|_{k}}({\mathcal{F}})$
by
![]() $\mathsf{A}_{X}^{k}({\mathcal{F}})$
. The abelian group
$\mathsf{A}_{X}^{k}({\mathcal{F}})$
. The abelian group
 $\unicode[STIX]{x1D6E4}(X,\mathsf{A}_{X}^{k}({\mathcal{F}}))$
will be denoted by
$\unicode[STIX]{x1D6E4}(X,\mathsf{A}_{X}^{k}({\mathcal{F}}))$
will be denoted by
![]() $\mathbb{A}_{X}^{k}({\mathcal{F}})$
.
$\mathbb{A}_{X}^{k}({\mathcal{F}})$
.
As the superscript indicates, these sheaves can be assembled into a co-simplicial object. The proof of this can be found in [Reference HuberHub91, Theorem 2.4.1].
Proposition 1.7. Let
![]() $X$
be a Noetherian scheme, and
$X$
be a Noetherian scheme, and
 $T_{\bullet }\subset |X|_{\bullet }$
a simplicial subset. There is an exact functor
$T_{\bullet }\subset |X|_{\bullet }$
a simplicial subset. There is an exact functor
 $\mathsf{A}_{X,T_{\bullet }}^{\bullet }:\mathsf{QCoh}(X)\rightarrow \mathsf{Fun}(\unicode[STIX]{x1D6E5},\mathsf{Mod}({\mathcal{O}}_{X}))$
, which commutes with directed colimits, and maps
$\mathsf{A}_{X,T_{\bullet }}^{\bullet }:\mathsf{QCoh}(X)\rightarrow \mathsf{Fun}(\unicode[STIX]{x1D6E5},\mathsf{Mod}({\mathcal{O}}_{X}))$
, which commutes with directed colimits, and maps
![]() $([k],{\mathcal{F}})$
to
$([k],{\mathcal{F}})$
to
 $\mathsf{A}_{X,T_{k}}({\mathcal{F}})$
. We denote the functor
$\mathsf{A}_{X,T_{k}}({\mathcal{F}})$
. We denote the functor
 $\unicode[STIX]{x1D6E4}(X,\mathsf{A}_{X,T_{\bullet }}^{\bullet }(-)):\mathsf{QCoh}(X)\rightarrow \mathsf{Fun}(\unicode[STIX]{x1D6E5},\mathsf{AbGrp})$
by
$\unicode[STIX]{x1D6E4}(X,\mathsf{A}_{X,T_{\bullet }}^{\bullet }(-)):\mathsf{QCoh}(X)\rightarrow \mathsf{Fun}(\unicode[STIX]{x1D6E5},\mathsf{AbGrp})$
by
 $\mathbb{A}_{X,T_{\bullet }}^{\bullet }(-)$
; it is exact and commutes with directed colimits. The notation
$\mathbb{A}_{X,T_{\bullet }}^{\bullet }(-)$
; it is exact and commutes with directed colimits. The notation
![]() $\mathbb{A}_{X}^{\bullet }(-)$
is reserved for the functor corresponding to the case
$\mathbb{A}_{X}^{\bullet }(-)$
is reserved for the functor corresponding to the case
 $T_{\bullet }=|X|_{\bullet }$
. We shall write
$T_{\bullet }=|X|_{\bullet }$
. We shall write
![]() $\mathbb{A}_{X}^{\bullet }$
to denote the co-simplicial ring obtained by applying this functor to the structure sheaf
$\mathbb{A}_{X}^{\bullet }$
to denote the co-simplicial ring obtained by applying this functor to the structure sheaf
![]() ${\mathcal{O}}_{X}$
.
${\mathcal{O}}_{X}$
.
Let
![]() $X$
be an irreducible Noetherian scheme of dimension 1, and
$X$
be an irreducible Noetherian scheme of dimension 1, and
![]() ${\mathcal{F}}$
a coherent sheaf on
${\mathcal{F}}$
a coherent sheaf on
![]() $X$
. We will discuss how the definitions above recover the classical theory of adèles for algebraic curves. Following classical conventions, we denote by
$X$
. We will discuss how the definitions above recover the classical theory of adèles for algebraic curves. Following classical conventions, we denote by
 $$\begin{eqnarray}\mathbb{A}_{X}({\mathcal{F}})=\mathop{\prod }_{x\in |X|_{\text{cl}}}^{\!\!\!\!\prime }\,\widehat{{\mathcal{F}}}_{x}\otimes _{\widehat{{\mathcal{O}}}_{x}}\operatorname{Frac}\widehat{{\mathcal{O}}}_{X},\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{A}_{X}({\mathcal{F}})=\mathop{\prod }_{x\in |X|_{\text{cl}}}^{\!\!\!\!\prime }\,\widehat{{\mathcal{F}}}_{x}\otimes _{\widehat{{\mathcal{O}}}_{x}}\operatorname{Frac}\widehat{{\mathcal{O}}}_{X},\end{eqnarray}$$
the restricted product ranging over all closed points
 $x\in |X|_{\text{cl}}$
. We denote by
$x\in |X|_{\text{cl}}$
. We denote by
 $$\begin{eqnarray}\mathbb{O}_{X}({\mathcal{F}})=\mathop{\prod }_{x\in X_{\text{cl}}}\widehat{{\mathcal{F}}}_{x};\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{O}_{X}({\mathcal{F}})=\mathop{\prod }_{x\in X_{\text{cl}}}\widehat{{\mathcal{F}}}_{x};\end{eqnarray}$$
and by
![]() $F_{X}({\mathcal{F}})$
the
$F_{X}({\mathcal{F}})$
the
![]() ${\mathcal{O}}$
-module
${\mathcal{O}}$
-module
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D702}}$
, where
${\mathcal{F}}_{\unicode[STIX]{x1D702}}$
, where
![]() $\unicode[STIX]{x1D702}$
is the generic point of
$\unicode[STIX]{x1D702}$
is the generic point of
![]() $X$
. With respect to this notation we may identify the co-simplicial
$X$
. With respect to this notation we may identify the co-simplicial
![]() ${\mathcal{O}}$
-module
${\mathcal{O}}$
-module
![]() $\mathbb{A}_{X}^{\bullet }({\mathcal{F}})$
with
$\mathbb{A}_{X}^{\bullet }({\mathcal{F}})$
with

where
 $F_{X}({\mathcal{F}})\rightarrow \mathbb{A}_{X}({\mathcal{F}})$
is the diagonal inclusion, and
$F_{X}({\mathcal{F}})\rightarrow \mathbb{A}_{X}({\mathcal{F}})$
is the diagonal inclusion, and
 $\mathbb{O}_{X}({\mathcal{F}})\rightarrow \mathbb{A}_{X}({\mathcal{F}})$
the canonical map. Embracing the usual redundancies in co-simplicial objects, that is the continual re-appearance of factors already seen at a lower degree level, we observe that Beilinson’s
$\mathbb{O}_{X}({\mathcal{F}})\rightarrow \mathbb{A}_{X}({\mathcal{F}})$
the canonical map. Embracing the usual redundancies in co-simplicial objects, that is the continual re-appearance of factors already seen at a lower degree level, we observe that Beilinson’s
![]() $\mathbb{A}_{X}^{\bullet }$
captures the classical theory of adèles.
$\mathbb{A}_{X}^{\bullet }$
captures the classical theory of adèles.
It is also helpful to understand the co-simplicial structure in the local case. Let
 $\unicode[STIX]{x1D70E}:[n]\rightarrow |X|_{{\leqslant}}$
be an element of
$\unicode[STIX]{x1D70E}:[n]\rightarrow |X|_{{\leqslant}}$
be an element of
![]() $|X|_{n}$
. We denote the ring of adèles
$|X|_{n}$
. We denote the ring of adèles
![]() $\mathbb{A}_{X,\{\unicode[STIX]{x1D70E}\}}$
corresponding to
$\mathbb{A}_{X,\{\unicode[STIX]{x1D70E}\}}$
corresponding to
 $T=\{\unicode[STIX]{x1D70E}\}\subset |X|_{n}$
by
$T=\{\unicode[STIX]{x1D70E}\}\subset |X|_{n}$
by
![]() $\mathbb{A}_{X,\unicode[STIX]{x1D70E}}$
. Proposition 1.7 implies that for every map
$\mathbb{A}_{X,\unicode[STIX]{x1D70E}}$
. Proposition 1.7 implies that for every map
 $f:[m]\rightarrow [n]$
in
$f:[m]\rightarrow [n]$
in
![]() $\unicode[STIX]{x1D6E5}$
we have a ring homomorphism
$\unicode[STIX]{x1D6E5}$
we have a ring homomorphism
 $\mathbb{A}_{X,\unicode[STIX]{x1D70E}\circ f}\rightarrow \mathbb{A}_{X,\unicode[STIX]{x1D70E}}$
. The following assertion is also proven in [Reference HuberHub91, Theorem 2.4.1].
$\mathbb{A}_{X,\unicode[STIX]{x1D70E}\circ f}\rightarrow \mathbb{A}_{X,\unicode[STIX]{x1D70E}}$
. The following assertion is also proven in [Reference HuberHub91, Theorem 2.4.1].
Lemma 1.8. Let
![]() $X$
and
$X$
and
![]() $T_{\bullet }$
be as in Proposition 1.7. The co-simplicial ring
$T_{\bullet }$
be as in Proposition 1.7. The co-simplicial ring
![]() $\mathbb{A}_{X,T_{\bullet }}^{\bullet }$
injects into the co-simplicial ring
$\mathbb{A}_{X,T_{\bullet }}^{\bullet }$
injects into the co-simplicial ring
 $$\begin{eqnarray}[n]\mapsto \mathop{\prod }_{\unicode[STIX]{x1D70E}:[n]\rightarrow |X|_{{\leqslant}}}\mathbb{A}_{X,\unicode[STIX]{x1D70E}}.\end{eqnarray}$$
$$\begin{eqnarray}[n]\mapsto \mathop{\prod }_{\unicode[STIX]{x1D70E}:[n]\rightarrow |X|_{{\leqslant}}}\mathbb{A}_{X,\unicode[STIX]{x1D70E}}.\end{eqnarray}$$
We also need the following observation, which is a consequence of the definitions of adèles.
Remark 1.9. If
![]() ${\mathcal{F}}$
is a quasi-coherent sheaf on
${\mathcal{F}}$
is a quasi-coherent sheaf on
![]() $X$
, set-theoretically supported on a finite union of closed points
$X$
, set-theoretically supported on a finite union of closed points
![]() $Z\subset X$
, then we have
$Z\subset X$
, then we have
 ${\mathcal{F}}\simeq \mathsf{A}_{X}^{k}({\mathcal{F}})$
.
${\mathcal{F}}\simeq \mathsf{A}_{X}^{k}({\mathcal{F}})$
.
Another observation which we will need is that for an affine Noetherian scheme
![]() $X$
, the functor
$X$
, the functor
 $$\begin{eqnarray}\mathbb{A}_{X,T}(-):\mathsf{QCoh}(X)\rightarrow \mathsf{Mod}(\unicode[STIX]{x1D6E4}({\mathcal{O}}_{X}))\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{A}_{X,T}(-):\mathsf{QCoh}(X)\rightarrow \mathsf{Mod}(\unicode[STIX]{x1D6E4}({\mathcal{O}}_{X}))\end{eqnarray}$$
can be expressed as
 $-\otimes _{\unicode[STIX]{x1D6E4}({\mathcal{O}}_{X})}\mathbb{A}_{X,T}$
. This is the case, since
$-\otimes _{\unicode[STIX]{x1D6E4}({\mathcal{O}}_{X})}\mathbb{A}_{X,T}$
. This is the case, since
 $\mathbb{A}_{X,T}(-)$
, and
$\mathbb{A}_{X,T}(-)$
, and
![]() $-\otimes -$
commute with filtered colimits. Since
$-\otimes -$
commute with filtered colimits. Since
 $\mathbb{A}_{X,T}(-)$
takes values in flasque sheaves by [Reference HuberHub91, Proposition 2.1.5] (see also Corollary 1.15), we see that
$\mathbb{A}_{X,T}(-)$
takes values in flasque sheaves by [Reference HuberHub91, Proposition 2.1.5] (see also Corollary 1.15), we see that
 $\mathbb{A}_{X,T}(-)$
is an exact functor. Therefore,
$\mathbb{A}_{X,T}(-)$
is an exact functor. Therefore,
![]() $\mathbb{A}_{X,T}$
is a flat algebra over
$\mathbb{A}_{X,T}$
is a flat algebra over
![]() $\unicode[STIX]{x1D6E4}({\mathcal{O}}_{X})$
. We record this for later use.
$\unicode[STIX]{x1D6E4}({\mathcal{O}}_{X})$
. We record this for later use.
Lemma 1.10. Let
 $X=\operatorname{Spec}R$
be an affine Noetherian scheme. Then
$X=\operatorname{Spec}R$
be an affine Noetherian scheme. Then
![]() $\mathbb{A}_{X,T}$
is a flat
$\mathbb{A}_{X,T}$
is a flat
![]() $R$
-algebra.
$R$
-algebra.
1.2 Functoriality
If
 $f:X\rightarrow Y$
is a morphism of Noetherian schemes, we have an induced map of partially ordered sets
$f:X\rightarrow Y$
is a morphism of Noetherian schemes, we have an induced map of partially ordered sets
 $|X|_{{\leqslant}}\rightarrow |Y|_{{\leqslant}}$
. Indeed,
$|X|_{{\leqslant}}\rightarrow |Y|_{{\leqslant}}$
. Indeed,
 $x\in \overline{\{y\}}$
implies
$x\in \overline{\{y\}}$
implies
 $f(x)\in \overline{\{f(y)\}}$
. In addition, we have an induced morphism of local rings
$f(x)\in \overline{\{f(y)\}}$
. In addition, we have an induced morphism of local rings
 ${\mathcal{O}}_{Y,f(x)}\rightarrow {\mathcal{O}}_{X,x}$
. These observations are the building blocks of a functoriality property satisfied by adèles. To the best of the author’s knowledge, this property has not yet been recorded in the literature.
${\mathcal{O}}_{Y,f(x)}\rightarrow {\mathcal{O}}_{X,x}$
. These observations are the building blocks of a functoriality property satisfied by adèles. To the best of the author’s knowledge, this property has not yet been recorded in the literature.
Lemma 1.11. Let
 $f:X\rightarrow Y$
be a morphism of Noetherian schemes, and
$f:X\rightarrow Y$
be a morphism of Noetherian schemes, and
 ${\mathcal{F}}\in \mathsf{QCoh}(Y)$
a quasi-coherent sheaf on
${\mathcal{F}}\in \mathsf{QCoh}(Y)$
a quasi-coherent sheaf on
![]() $Y$
. For
$Y$
. For
 $T\subset |X|_{n}$
and
$T\subset |X|_{n}$
and
 $f(T)\subset T^{\prime }\subset |Y|_{n}$
we have a morphism
$f(T)\subset T^{\prime }\subset |Y|_{n}$
we have a morphism
 $\mathsf{A}_{Y,T^{\prime }}({\mathcal{F}})\rightarrow f_{\ast }\mathsf{A}_{X,T}(f^{\ast }{\mathcal{F}})$
in
$\mathsf{A}_{Y,T^{\prime }}({\mathcal{F}})\rightarrow f_{\ast }\mathsf{A}_{X,T}(f^{\ast }{\mathcal{F}})$
in
 $\mathsf{Mod}({\mathcal{O}}_{Y})$
, fitting into the following commutative diagram.
$\mathsf{Mod}({\mathcal{O}}_{Y})$
, fitting into the following commutative diagram.

Commutativity of this diagram amounts to the construction inducing a map of augmented co-simplicial objects in
 $\mathsf{Mod}({\mathcal{O}}_{Y})$
from
$\mathsf{Mod}({\mathcal{O}}_{Y})$
from
 ${\mathcal{F}}\rightarrow \mathsf{A}_{Y}^{\bullet }({\mathcal{F}})$
to
${\mathcal{F}}\rightarrow \mathsf{A}_{Y}^{\bullet }({\mathcal{F}})$
to
 $f_{\ast }f^{\ast }{\mathcal{F}}\rightarrow f_{\ast }\mathsf{A}_{X}^{\bullet }(f^{\ast }{\mathcal{F}})$
.
$f_{\ast }f^{\ast }{\mathcal{F}}\rightarrow f_{\ast }\mathsf{A}_{X}^{\bullet }(f^{\ast }{\mathcal{F}})$
.
Proof of Lemma 1.11.
The morphism
 $\mathsf{A}_{Y,T^{\prime }}({\mathcal{F}})\rightarrow f_{\ast }\mathsf{A}_{X,T}(f^{\ast }{\mathcal{F}})$
is constructed by induction on
$\mathsf{A}_{Y,T^{\prime }}({\mathcal{F}})\rightarrow f_{\ast }\mathsf{A}_{X,T}(f^{\ast }{\mathcal{F}})$
is constructed by induction on
![]() $n$
(where
$n$
(where
 $T\subset |X|_{n}$
). For
$T\subset |X|_{n}$
). For
![]() $n=0$
and
$n=0$
and
 ${\mathcal{F}}\in \mathsf{Coh}(Y)$
, we have
${\mathcal{F}}\in \mathsf{Coh}(Y)$
, we have
 $$\begin{eqnarray}\mathsf{A}_{X,T}(f^{\ast }{\mathcal{F}})=\mathop{\prod }_{x\in T}\underset{r\geqslant 0}{\mathsf{lim}}(j_{rx})_{\ast }j_{rx}^{\ast }f^{\ast }{\mathcal{F}},\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{A}_{X,T}(f^{\ast }{\mathcal{F}})=\mathop{\prod }_{x\in T}\underset{r\geqslant 0}{\mathsf{lim}}(j_{rx})_{\ast }j_{rx}^{\ast }f^{\ast }{\mathcal{F}},\end{eqnarray}$$
and
 $\mathsf{A}_{Y,T^{\prime }}{\twoheadrightarrow}\mathsf{A}_{Y,f(T)}({\mathcal{F}})=\prod _{x\in f(T)}\mathsf{lim}_{r\geqslant 0}(j_{rx})_{\ast }j_{rx}^{\ast }{\mathcal{F}}$
. We have a map
$\mathsf{A}_{Y,T^{\prime }}{\twoheadrightarrow}\mathsf{A}_{Y,f(T)}({\mathcal{F}})=\prod _{x\in f(T)}\mathsf{lim}_{r\geqslant 0}(j_{rx})_{\ast }j_{rx}^{\ast }{\mathcal{F}}$
. We have a map
 $$\begin{eqnarray}{\mathcal{F}}\otimes _{{\mathcal{O}}_{Y}}{\mathcal{O}}_{Y,f(x)}\rightarrow f^{\ast }{\mathcal{F}}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{X,x}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}\otimes _{{\mathcal{O}}_{Y}}{\mathcal{O}}_{Y,f(x)}\rightarrow f^{\ast }{\mathcal{F}}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{X,x}\end{eqnarray}$$
for each
![]() $x\in T$
, which defines the required map for
$x\in T$
, which defines the required map for
 $T\subset |X|_{0}$
.
$T\subset |X|_{0}$
.
Assume that the morphism
 $\mathsf{A}_{Y,T^{\prime }}({\mathcal{F}})\rightarrow f_{\ast }\mathsf{A}_{X,T}(f^{\ast }{\mathcal{F}})$
has been constructed for all
$\mathsf{A}_{Y,T^{\prime }}({\mathcal{F}})\rightarrow f_{\ast }\mathsf{A}_{X,T}(f^{\ast }{\mathcal{F}})$
has been constructed for all
 $T\subset |X|_{k}$
and
$T\subset |X|_{k}$
and
 $f(T)\subset T^{\prime }\subset |Y|_{k}$
, where
$f(T)\subset T^{\prime }\subset |Y|_{k}$
, where
![]() $k\leqslant n$
, such that we have the following commutative diagram.
$k\leqslant n$
, such that we have the following commutative diagram.

Let
 $T\subset |X|_{n+1}$
. For every
$T\subset |X|_{n+1}$
. For every
![]() $x\in X$
, we then have a well-defined map
$x\in X$
, we then have a well-defined map
 $\mathsf{A}_{Y,\text{}_{f(x)}f(T)}({\mathcal{F}})\rightarrow f_{\ast }\mathsf{A}_{X,\text{}_{x}T}(f^{\ast }{\mathcal{F}})$
, since
$\mathsf{A}_{Y,\text{}_{f(x)}f(T)}({\mathcal{F}})\rightarrow f_{\ast }\mathsf{A}_{X,\text{}_{x}T}(f^{\ast }{\mathcal{F}})$
, since
 $f(\text{}_{x}T)\subset \text{}_{f(x)}f(T)\subset \text{}_{f(x)}T^{\prime }$
. This induces a morphism
$f(\text{}_{x}T)\subset \text{}_{f(x)}f(T)\subset \text{}_{f(x)}T^{\prime }$
. This induces a morphism
 $$\begin{eqnarray}\mathop{\prod }_{x\in |X|}\underset{r\geqslant 0}{\mathsf{lim}}\mathsf{A}_{Y,\text{}_{f(x)}f(T)}((j_{rf(x)})_{\ast }j_{rf(x)}^{\ast }f^{\ast }{\mathcal{F}})\rightarrow \mathop{\prod }_{x\in |X|}\underset{r\geqslant 0}{\mathsf{lim}}\mathsf{A}_{X,\text{}_{x}T}((j_{rx})_{\ast }j_{rx}^{\ast }f^{\ast }{\mathcal{F}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{x\in |X|}\underset{r\geqslant 0}{\mathsf{lim}}\mathsf{A}_{Y,\text{}_{f(x)}f(T)}((j_{rf(x)})_{\ast }j_{rf(x)}^{\ast }f^{\ast }{\mathcal{F}})\rightarrow \mathop{\prod }_{x\in |X|}\underset{r\geqslant 0}{\mathsf{lim}}\mathsf{A}_{X,\text{}_{x}T}((j_{rx})_{\ast }j_{rx}^{\ast }f^{\ast }{\mathcal{F}}).\end{eqnarray}$$
We have a commutative diagram

which commutes levelwise (before taking the inverse limits and products) by the induction hypothesis.
We precompose the map (1) with
 $$\begin{eqnarray}\displaystyle \mathop{\prod }_{y\in |Y|}\underset{r\geqslant 0}{\mathsf{lim}}\mathsf{A}_{Y,\text{}_{y}T^{\prime }}((j_{ry})_{\ast }j_{ry}^{\ast }f^{\ast }{\mathcal{F}}) & {\twoheadrightarrow} & \displaystyle \mathop{\prod }_{y\in f(|X|)}\underset{r\geqslant 0}{\mathsf{lim}}\mathsf{A}_{Y,\text{}_{y}T^{\prime }}((j_{ry})_{\ast }j_{ry}^{\ast }f^{\ast }{\mathcal{F}})\nonumber\\ \displaystyle & \rightarrow & \displaystyle \mathop{\prod }_{x\in |X|}\underset{r\geqslant 0}{\mathsf{lim}}\mathsf{A}_{Y,\text{}_{f(x)}f(T)}((j_{rf(x)})_{\ast }j_{rf(x)}^{\ast }f^{\ast }{\mathcal{F}})\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{y\in |Y|}\underset{r\geqslant 0}{\mathsf{lim}}\mathsf{A}_{Y,\text{}_{y}T^{\prime }}((j_{ry})_{\ast }j_{ry}^{\ast }f^{\ast }{\mathcal{F}}) & {\twoheadrightarrow} & \displaystyle \mathop{\prod }_{y\in f(|X|)}\underset{r\geqslant 0}{\mathsf{lim}}\mathsf{A}_{Y,\text{}_{y}T^{\prime }}((j_{ry})_{\ast }j_{ry}^{\ast }f^{\ast }{\mathcal{F}})\nonumber\\ \displaystyle & \rightarrow & \displaystyle \mathop{\prod }_{x\in |X|}\underset{r\geqslant 0}{\mathsf{lim}}\mathsf{A}_{Y,\text{}_{f(x)}f(T)}((j_{rf(x)})_{\ast }j_{rf(x)}^{\ast }f^{\ast }{\mathcal{F}})\end{eqnarray}$$
to obtain the required morphism
 $\mathsf{A}_{Y,T^{\prime }}({\mathcal{F}})\rightarrow f_{\ast }\mathsf{A}_{X,T}(f^{\ast }{\mathcal{F}})$
. The required commutativity assumption holds by commutativity of (2).◻
$\mathsf{A}_{Y,T^{\prime }}({\mathcal{F}})\rightarrow f_{\ast }\mathsf{A}_{X,T}(f^{\ast }{\mathcal{F}})$
. The required commutativity assumption holds by commutativity of (2).◻
Setting
 ${\mathcal{F}}={\mathcal{O}}_{Y}$
in the assertion above, we obtain the following result as a consequence.
${\mathcal{F}}={\mathcal{O}}_{Y}$
in the assertion above, we obtain the following result as a consequence.
Corollary 1.12. For a morphism of Noetherian schemes, we obtain a map of augmented co-simplicial objects

in sheaves of algebras on the topological space
![]() $|Y|$
.
$|Y|$
.
Taking global sections, we obtain a functor from Noetherian schemes to co-simplicial rings.
Definition 1.13. We denote the functor
 $(\mathsf{Sch}^{\mathsf{N}})^{\mathsf{op}}\rightarrow (\mathsf{Rng}^{\unicode[STIX]{x1D6E5}})$
, sending a Noetherian scheme
$(\mathsf{Sch}^{\mathsf{N}})^{\mathsf{op}}\rightarrow (\mathsf{Rng}^{\unicode[STIX]{x1D6E5}})$
, sending a Noetherian scheme
![]() $X$
to the co-simplicial ring
$X$
to the co-simplicial ring
 $\mathbb{A}_{X}^{\bullet }({\mathcal{O}}_{X})$
by
$\mathbb{A}_{X}^{\bullet }({\mathcal{O}}_{X})$
by
![]() $\mathbb{A}^{\bullet }$
.
$\mathbb{A}^{\bullet }$
.
As we have alluded to in Theorem 0.4, and will prove as Corollary 3.32, this functor has a left-inverse.
1.3 Taking a closer look at the flasque sheaf of adèles
In this subsection we give a close analysis of flasqueness of the sheaf
 $\mathsf{A}_{X,T}({\mathcal{F}})$
. We show that the restriction map
$\mathsf{A}_{X,T}({\mathcal{F}})$
. We show that the restriction map
 $\mathbb{A}_{X,T}({\mathcal{F}})\rightarrow \mathbb{A}_{U,T\cap |U|_{n}}({\mathcal{F}})$
is not only surjective, but admits an
$\mathbb{A}_{X,T}({\mathcal{F}})\rightarrow \mathbb{A}_{U,T\cap |U|_{n}}({\mathcal{F}})$
is not only surjective, but admits an
 $\mathbb{A}_{X,T}({\mathcal{O}}_{X})$
-linear section. As a consequence we obtain that
$\mathbb{A}_{X,T}({\mathcal{O}}_{X})$
-linear section. As a consequence we obtain that
 $\mathsf{A}_{X,T}({\mathcal{O}}_{X})$
is what we call a lâche sheaf of algebras in Definition 2.9 (see also Corollary 2.17). A similar statement is contained in [Reference HuberHub91, Proposition 2.1.5], however the
$\mathsf{A}_{X,T}({\mathcal{O}}_{X})$
is what we call a lâche sheaf of algebras in Definition 2.9 (see also Corollary 2.17). A similar statement is contained in [Reference HuberHub91, Proposition 2.1.5], however the
 $\mathsf{A}_{X,T}({\mathcal{O}}_{X})$
-linearity is not investigated in [Reference HuberHub91].
$\mathsf{A}_{X,T}({\mathcal{O}}_{X})$
-linearity is not investigated in [Reference HuberHub91].
Lemma 1.14. Let
![]() $X$
be a Noetherian scheme,
$X$
be a Noetherian scheme,
 $T\subset |X|_{n}$
and
$T\subset |X|_{n}$
and
![]() ${\mathcal{F}}$
a quasi-coherent sheaf on
${\mathcal{F}}$
a quasi-coherent sheaf on
![]() $X$
. For every open subset
$X$
. For every open subset
![]() $U\subset X$
the restriction map
$U\subset X$
the restriction map
 $\mathbb{A}_{X,T}({\mathcal{F}})\rightarrow \mathbb{A}_{U,T}({\mathcal{F}})$
has a section, which is moreover
$\mathbb{A}_{X,T}({\mathcal{F}})\rightarrow \mathbb{A}_{U,T}({\mathcal{F}})$
has a section, which is moreover
 $\mathbb{A}_{X,T}({\mathcal{O}}_{X})$
-linear and functorial in
$\mathbb{A}_{X,T}({\mathcal{O}}_{X})$
-linear and functorial in
![]() ${\mathcal{F}}$
.
${\mathcal{F}}$
.
Proof. We denote the inclusion
 $U{\hookrightarrow}X$
by
$U{\hookrightarrow}X$
by
![]() $j$
, and will construct a section to the map of sheaves
$j$
, and will construct a section to the map of sheaves
 $\mathsf{A}_{X,T}({\mathcal{F}})\rightarrow j_{\ast }\mathsf{A}_{U,T}({\mathcal{F}})$
. Recall that for a coherent sheaf
$\mathsf{A}_{X,T}({\mathcal{F}})\rightarrow j_{\ast }\mathsf{A}_{U,T}({\mathcal{F}})$
. Recall that for a coherent sheaf
![]() ${\mathcal{F}}$
we have an equivalence
${\mathcal{F}}$
we have an equivalence
 $\mathsf{A}_{X,T}({\mathcal{F}})\simeq \prod _{x\in X}\mathop{\varprojlim }\nolimits_{r}\mathsf{A}_{X,\text{}_{x}T}(j_{rx}^{\ast }{\mathcal{F}}),$
and
$\mathsf{A}_{X,T}({\mathcal{F}})\simeq \prod _{x\in X}\mathop{\varprojlim }\nolimits_{r}\mathsf{A}_{X,\text{}_{x}T}(j_{rx}^{\ast }{\mathcal{F}}),$
and
 $j_{\ast }\mathsf{A}_{U,T\cap |U|_{n}}({\mathcal{F}})\simeq \prod _{x\in U}\mathop{\varprojlim }\nolimits_{r}\mathsf{A}_{U,\text{}_{x}T\cap |U|_{n-1}}(j_{rx}^{\ast }{\mathcal{F}}).$
Suppose that we have already constructed a section
$j_{\ast }\mathsf{A}_{U,T\cap |U|_{n}}({\mathcal{F}})\simeq \prod _{x\in U}\mathop{\varprojlim }\nolimits_{r}\mathsf{A}_{U,\text{}_{x}T\cap |U|_{n-1}}(j_{rx}^{\ast }{\mathcal{F}}).$
Suppose that we have already constructed a section
![]() $\unicode[STIX]{x1D719}_{{\mathcal{F}}}$
for
$\unicode[STIX]{x1D719}_{{\mathcal{F}}}$
for
 $\mathsf{A}_{X,T^{\prime }}({\mathcal{F}})\rightarrow j_{\ast }\mathsf{A}_{U,T^{\prime }}({\mathcal{F}})$
for
$\mathsf{A}_{X,T^{\prime }}({\mathcal{F}})\rightarrow j_{\ast }\mathsf{A}_{U,T^{\prime }}({\mathcal{F}})$
for
 $T^{\prime }\subset |X|_{n-1}$
, such that for each map
$T^{\prime }\subset |X|_{n-1}$
, such that for each map
![]() ${\mathcal{F}}\rightarrow {\mathcal{G}}$
we obtain the following commutative square.
${\mathcal{F}}\rightarrow {\mathcal{G}}$
we obtain the following commutative square.

We can then map the limit
 $\prod _{x\in U}\mathop{\varprojlim }\nolimits_{r}\mathsf{A}_{U}(\text{}_{x}T;j_{rx}^{\ast }{\mathcal{F}})$
to
$\prod _{x\in U}\mathop{\varprojlim }\nolimits_{r}\mathsf{A}_{U}(\text{}_{x}T;j_{rx}^{\ast }{\mathcal{F}})$
to
 $\prod _{x\in X}\mathop{\varprojlim }\nolimits_{r}\mathsf{A}_{U}(\text{}_{x}T;j_{rx}^{\ast }{\mathcal{F}})$
, by defining the components of the map to be
$\prod _{x\in X}\mathop{\varprojlim }\nolimits_{r}\mathsf{A}_{U}(\text{}_{x}T;j_{rx}^{\ast }{\mathcal{F}})$
, by defining the components of the map to be
![]() $0$
for
$0$
for
 $x\in X\setminus U$
, and given by the section
$x\in X\setminus U$
, and given by the section
![]() $\unicode[STIX]{x1D719}$
otherwise.
$\unicode[STIX]{x1D719}$
otherwise.
By induction we see that we may assume that
 $T\subset |X|_{0}$
. We may also assume that
$T\subset |X|_{0}$
. We may also assume that
![]() ${\mathcal{F}}$
is coherent. Hence,
${\mathcal{F}}$
is coherent. Hence,
 $\mathsf{A}_{X,T}({\mathcal{F}})$
is equal to the product
$\mathsf{A}_{X,T}({\mathcal{F}})$
is equal to the product
 $\prod _{x\in T}\mathop{\varprojlim }\nolimits_{r}j_{rx}^{\ast }{\mathcal{F}}$
, and
$\prod _{x\in T}\mathop{\varprojlim }\nolimits_{r}j_{rx}^{\ast }{\mathcal{F}}$
, and
 $\mathsf{A}_{U}(T,{\mathcal{F}})$
to
$\mathsf{A}_{U}(T,{\mathcal{F}})$
to
 $\prod _{x\in T\cap U}\mathop{\varprojlim }\nolimits_{r}j_{rx}^{\ast }{\mathcal{F}}$
. The natural restriction map is given by the canonical projection. A canonical section with the required properties is given by the identity map for components corresponding to
$\prod _{x\in T\cap U}\mathop{\varprojlim }\nolimits_{r}j_{rx}^{\ast }{\mathcal{F}}$
. The natural restriction map is given by the canonical projection. A canonical section with the required properties is given by the identity map for components corresponding to
 $x\in U\cap T$
, and the map 0 for
$x\in U\cap T$
, and the map 0 for
 $x\in T\setminus U$
.◻
$x\in T\setminus U$
.◻
As a corollary one obtains the following observation of Beilinson.
Corollary 1.15. The sheaves
 $\mathbb{A}_{X,T}({\mathcal{F}})$
are flasque.
$\mathbb{A}_{X,T}({\mathcal{F}})$
are flasque.
In [Reference BeilinsonBei80] Beilinson continues to observe that for any quasi-coherent sheaf
![]() ${\mathcal{F}}$
the canonical augmentation
${\mathcal{F}}$
the canonical augmentation
 ${\mathcal{F}}\rightarrow \mathsf{A}_{X}^{\bullet }({\mathcal{F}})$
induces an equivalence
${\mathcal{F}}\rightarrow \mathsf{A}_{X}^{\bullet }({\mathcal{F}})$
induces an equivalence
 ${\mathcal{F}}\simeq |\mathsf{A}_{X}^{\bullet }({\mathcal{F}})|$
. A detailed proof is given by Huber [Reference HuberHub91, Theorem 4.1.1].
${\mathcal{F}}\simeq |\mathsf{A}_{X}^{\bullet }({\mathcal{F}})|$
. A detailed proof is given by Huber [Reference HuberHub91, Theorem 4.1.1].
Theorem 1.16 (Beilinson).
Let
![]() $X$
be a Noetherian scheme and
$X$
be a Noetherian scheme and
![]() ${\mathcal{F}}$
a quasi-coherent sheaf on
${\mathcal{F}}$
a quasi-coherent sheaf on
![]() $X$
. The augmentation
$X$
. The augmentation
 ${\mathcal{F}}\rightarrow \mathsf{A}_{X}^{\bullet }({\mathcal{F}})$
defines a co-simplicial resolution of
${\mathcal{F}}\rightarrow \mathsf{A}_{X}^{\bullet }({\mathcal{F}})$
defines a co-simplicial resolution of
![]() ${\mathcal{F}}$
by flasque
${\mathcal{F}}$
by flasque
![]() ${\mathcal{O}}_{X}$
-modules. Applying the global sections functor
${\mathcal{O}}_{X}$
-modules. Applying the global sections functor
 $\unicode[STIX]{x1D6E4}(X,-)$
we obtain
$\unicode[STIX]{x1D6E4}(X,-)$
we obtain
 $R\unicode[STIX]{x1D6E4}(X,{\mathcal{F}})=|\mathbb{A}_{X}^{\bullet }({\mathcal{F}})|$
, where the co-simplicial realisation
$R\unicode[STIX]{x1D6E4}(X,{\mathcal{F}})=|\mathbb{A}_{X}^{\bullet }({\mathcal{F}})|$
, where the co-simplicial realisation
![]() $|\cdot |$
is taken in the derived
$|\cdot |$
is taken in the derived
![]() $\infty$
-category
$\infty$
-category
 $\mathsf{D}(\mathsf{AbGrp})$
of abelian groups.
$\mathsf{D}(\mathsf{AbGrp})$
of abelian groups.
It is instructive to test the general considerations above on the special case of algebraic curves. For the rest of this subsection we will thus assume that
![]() $X$
is an algebraic curve. We denote by
$X$
is an algebraic curve. We denote by
![]() $\mathsf{A}_{X}$
the sheaf, assigning to an open subset
$\mathsf{A}_{X}$
the sheaf, assigning to an open subset
![]() $U\subset X$
the ring of adèles
$U\subset X$
the ring of adèles
![]() $\mathbb{A}_{U}$
. Similarly we have sheaves
$\mathbb{A}_{U}$
. Similarly we have sheaves
![]() $\mathsf{F}_{X}$
and
$\mathsf{F}_{X}$
and
![]() $\mathsf{O}_{X}$
of rational functions and integral adèles.
$\mathsf{O}_{X}$
of rational functions and integral adèles.
The sheaves
![]() $\mathsf{A}_{X}$
and
$\mathsf{A}_{X}$
and
![]() $\mathsf{O}_{X}$
satisfy the conclusion of Lemma 1.14, because a section over
$\mathsf{O}_{X}$
satisfy the conclusion of Lemma 1.14, because a section over
![]() $U\subset X$
can be extended by 0, outside of
$U\subset X$
can be extended by 0, outside of
![]() $U$
. Since
$U$
. Since
 $\mathsf{F}_{X}(U)=\mathsf{F}_{X}(X)$
, as long as
$\mathsf{F}_{X}(U)=\mathsf{F}_{X}(X)$
, as long as
![]() $U\neq \emptyset$
, we see that the conclusion of Lemma 1.14 is trivially satisfied for
$U\neq \emptyset$
, we see that the conclusion of Lemma 1.14 is trivially satisfied for
![]() $\mathsf{F}$
. Beilinson’s Theorem 1.16 is in the present situation tantamount to the assertion that the complex
$\mathsf{F}$
. Beilinson’s Theorem 1.16 is in the present situation tantamount to the assertion that the complex
 $$\begin{eqnarray}[{\mathcal{O}}_{X}\rightarrow \mathsf{F}_{X}\oplus \mathsf{O}_{X}\rightarrow \mathsf{A}_{X}]\end{eqnarray}$$
$$\begin{eqnarray}[{\mathcal{O}}_{X}\rightarrow \mathsf{F}_{X}\oplus \mathsf{O}_{X}\rightarrow \mathsf{A}_{X}]\end{eqnarray}$$
is exact. In other words, we observe that a rational function without any poles on
![]() $U\subset X$
, defines a regular function on
$U\subset X$
, defines a regular function on
![]() $U$
. While this is a tautology in the one-dimensional case, the general setting of Noetherian schemes requires more subtle arguments from commutative algebra. We refer the reader to the proof of [Reference HuberHub91, Theorem 4.1.1] for more details.
$U$
. While this is a tautology in the one-dimensional case, the general setting of Noetherian schemes requires more subtle arguments from commutative algebra. We refer the reader to the proof of [Reference HuberHub91, Theorem 4.1.1] for more details.
2 Perfect complexes and lâche sheaves of algebras
In this section we introduce the notion of lâche sheaves of algebras and prove Theorem 0.5.
2.1 Lâche sheaves of algebras
The main example of a lâche sheaf of algebras
![]() $\mathsf{A}$
is Beilinson’s sheaf of adèles. This is the content of Corollary 2.17 below.
$\mathsf{A}$
is Beilinson’s sheaf of adèles. This is the content of Corollary 2.17 below.
2.1.1 Flasque sheaves
In this section we record a few well-known lemmas on flasque sheaves for the convenience of the reader.
Lemma 2.1. If
![]() ${\mathcal{F}}$
is a sheaf on
${\mathcal{F}}$
is a sheaf on
![]() $X$
, such that every point
$X$
, such that every point
![]() $x\in X$
has an open neighbourhood
$x\in X$
has an open neighbourhood
![]() $U$
with
$U$
with
![]() ${\mathcal{F}}|_{U}$
flasque, then
${\mathcal{F}}|_{U}$
flasque, then
![]() ${\mathcal{F}}$
is a flasque sheaf.
${\mathcal{F}}$
is a flasque sheaf.
Proof. Let
![]() $V\subset X$
be an open subset and
$V\subset X$
be an open subset and
 $s\in {\mathcal{F}}(V)$
a section. We claim that there exists
$s\in {\mathcal{F}}(V)$
a section. We claim that there exists
 $t\in {\mathcal{F}}(X)$
with
$t\in {\mathcal{F}}(X)$
with
![]() $t|_{V}=s$
. Consider the set
$t|_{V}=s$
. Consider the set
![]() $I$
of pairs
$I$
of pairs
![]() $(W,t)$
, where
$(W,t)$
, where
 $W\subset X$
is an open subset containing
$W\subset X$
is an open subset containing
![]() $V$
, and
$V$
, and
 $t\in {\mathcal{F}}(W)$
, such that
$t\in {\mathcal{F}}(W)$
, such that
![]() $t|_{V}=s$
. Inclusion of open subsets induces a partial ordering on
$t|_{V}=s$
. Inclusion of open subsets induces a partial ordering on
![]() $I$
, where we say that
$I$
, where we say that
 $(W,t)\leqslant (W^{\prime },t^{\prime })$
if
$(W,t)\leqslant (W^{\prime },t^{\prime })$
if
 $W\subset W^{\prime }$
, and
$W\subset W^{\prime }$
, and
 $t^{\prime }|_{W}=t$
. Moreover,
$t^{\prime }|_{W}=t$
. Moreover,
![]() $I$
is inductively ordered, that is, for every totally ordered subposet
$I$
is inductively ordered, that is, for every totally ordered subposet
![]() $J\subset I$
, there exists a common upper bound
$J\subset I$
, there exists a common upper bound
![]() $i\in I$
, such that we have
$i\in I$
, such that we have
![]() $i\geqslant j$
for all
$i\geqslant j$
for all
![]() $j\in J$
. Indeed, denoting the pair corresponding to
$j\in J$
. Indeed, denoting the pair corresponding to
![]() $j\in J$
by
$j\in J$
by
![]() $(W_{j},t_{j})$
, we have
$(W_{j},t_{j})$
, we have
 $W_{j}\subset W_{k}$
for
$W_{j}\subset W_{k}$
for
![]() $j\leqslant k$
in
$j\leqslant k$
in
![]() $J$
, and
$J$
, and
 $t_{k}|_{W_{j}}=t_{j}$
. If we define
$t_{k}|_{W_{j}}=t_{j}$
. If we define
 $W=\bigcup _{j\in J}W_{j}$
, the fact that
$W=\bigcup _{j\in J}W_{j}$
, the fact that
![]() ${\mathcal{F}}$
is a sheaf allows us to define a section
${\mathcal{F}}$
is a sheaf allows us to define a section
 $t\in {\mathcal{F}}(W)$
with
$t\in {\mathcal{F}}(W)$
with
 $t|_{W_{j}}=t_{j}$
. In particular,
$t|_{W_{j}}=t_{j}$
. In particular,
 $(W,t)\in I$
is a common upper bound for the elements of
$(W,t)\in I$
is a common upper bound for the elements of
![]() $J$
.
$J$
.
Zorn’s lemma implies that the poset
![]() $I$
has a maximal element
$I$
has a maximal element
![]() $(W,t)$
. It remains to show that
$(W,t)$
. It remains to show that
 $W=X$
. Assume that there exists
$W=X$
. Assume that there exists
 $x\in X\setminus W$
. By assumption,
$x\in X\setminus W$
. By assumption,
![]() $x$
has an open neighbourhood
$x$
has an open neighbourhood
![]() $U$
, such that
$U$
, such that
![]() ${\mathcal{F}}|_{U}$
is flasque. In particular, there exists a section
${\mathcal{F}}|_{U}$
is flasque. In particular, there exists a section
 $r\in {\mathcal{F}}(U)$
, such that
$r\in {\mathcal{F}}(U)$
, such that
 $r|_{U\cap W}=t|_{U\cap W}$
. By virtue of the sheaf property we obtain a section
$r|_{U\cap W}=t|_{U\cap W}$
. By virtue of the sheaf property we obtain a section
 $t^{\prime }\in {\mathcal{F}}(W\cup U)$
, satisfying
$t^{\prime }\in {\mathcal{F}}(W\cup U)$
, satisfying
 $t^{\prime }|_{W}=t$
, which contradicts maximality of
$t^{\prime }|_{W}=t$
, which contradicts maximality of
![]() $(W,t)$
.◻
$(W,t)$
.◻
Lemma 2.2. If
![]() $X$
is a quasi-compact topological space and
$X$
is a quasi-compact topological space and
![]() $\mathsf{A}$
a sheaf of algebras, then every locally finitely generated
$\mathsf{A}$
a sheaf of algebras, then every locally finitely generated
![]() $\mathsf{A}$
-module
$\mathsf{A}$
-module
![]() $\mathsf{M}$
which is flasque is globally finitely generated, that is there exists a surjection
$\mathsf{M}$
which is flasque is globally finitely generated, that is there exists a surjection
 $\mathsf{A}^{n}\rightarrow \mathsf{M}$
.
$\mathsf{A}^{n}\rightarrow \mathsf{M}$
.
Proof. For every point
![]() $x\in X$
there exists a neighbourhood
$x\in X$
there exists a neighbourhood
![]() $U_{x}$
, such that
$U_{x}$
, such that
![]() $\mathsf{M}|_{U_{x}}$
is finitely generated. Since
$\mathsf{M}|_{U_{x}}$
is finitely generated. Since
![]() $X$
is quasi-compact, we may choose a finite subcover
$X$
is quasi-compact, we may choose a finite subcover
 $X=\bigcup _{i=1}^{n}U_{i}$
, and generating sections
$X=\bigcup _{i=1}^{n}U_{i}$
, and generating sections
 $(s_{ij})_{j=1,\ldots n_{i}}$
. Because
$(s_{ij})_{j=1,\ldots n_{i}}$
. Because
![]() $\mathsf{M}$
is assumed to be flasque, we may extend each
$\mathsf{M}$
is assumed to be flasque, we may extend each
![]() $s_{ij}$
to a global section
$s_{ij}$
to a global section
![]() $t_{ij}$
, and see that this finite subset of
$t_{ij}$
, and see that this finite subset of
 $\unicode[STIX]{x1D6E4}(X,\mathsf{M})$
generates
$\unicode[STIX]{x1D6E4}(X,\mathsf{M})$
generates
![]() $\mathsf{M}$
.◻
$\mathsf{M}$
.◻
Lemma 2.3. Assume that we have a short exact sequence of
![]() $\mathsf{A}$
-modules with
$\mathsf{A}$
-modules with
 $$\begin{eqnarray}0\rightarrow \mathsf{M}_{2}\rightarrow \mathsf{M}_{1}\rightarrow \mathsf{M}_{0}\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \mathsf{M}_{2}\rightarrow \mathsf{M}_{1}\rightarrow \mathsf{M}_{0}\rightarrow 0,\end{eqnarray}$$
with
![]() $\mathsf{M}_{i}$
flasque for
$\mathsf{M}_{i}$
flasque for
![]() $i>0$
, then
$i>0$
, then
![]() $\mathsf{M}_{0}$
is flasque as well.
$\mathsf{M}_{0}$
is flasque as well.
Proof. Since flasque sheaves have no higher cohomology, we have
 $H^{1}(X,\mathsf{M}_{2})=0$
, and therefore the following commutative diagram has exact rows
$H^{1}(X,\mathsf{M}_{2})=0$
, and therefore the following commutative diagram has exact rows

Commutativity of the right-hand square, and the fact that
 $\mathsf{M}_{1}(X){\twoheadrightarrow}\mathsf{M}_{1}(U){\twoheadrightarrow}\mathsf{M}_{0}(U)$
is surjective, implies surjectivity of
$\mathsf{M}_{1}(X){\twoheadrightarrow}\mathsf{M}_{1}(U){\twoheadrightarrow}\mathsf{M}_{0}(U)$
is surjective, implies surjectivity of
 $\mathsf{M}_{0}(X){\twoheadrightarrow}\mathsf{M}_{0}(U)$
.◻
$\mathsf{M}_{0}(X){\twoheadrightarrow}\mathsf{M}_{0}(U)$
.◻
Lemma 2.4. Let
![]() $\mathsf{A}$
be an arbitrary sheaf of algebras on a topological space
$\mathsf{A}$
be an arbitrary sheaf of algebras on a topological space
![]() $X$
. Consider the abelian category of sheaves of
$X$
. Consider the abelian category of sheaves of
![]() $\mathsf{A}$
-modules. The full subcategory, given by
$\mathsf{A}$
-modules. The full subcategory, given by
![]() $\mathsf{A}$
-modules
$\mathsf{A}$
-modules
![]() $\mathsf{M}$
, such that
$\mathsf{M}$
, such that
![]() $\mathsf{M}$
is a flasque sheaf, is extension-closed.
$\mathsf{M}$
is a flasque sheaf, is extension-closed.
Proof. Assume that we have a short exact sequence of
![]() $\mathsf{A}$
-modules
$\mathsf{A}$
-modules
 $\mathsf{M}_{1}{\hookrightarrow}\mathsf{M}_{2}{\twoheadrightarrow}\mathsf{M}_{3}$
, with
$\mathsf{M}_{1}{\hookrightarrow}\mathsf{M}_{2}{\twoheadrightarrow}\mathsf{M}_{3}$
, with
![]() $\mathsf{M}_{i}$
flasque for
$\mathsf{M}_{i}$
flasque for
![]() $i=1$
and
$i=1$
and
![]() $i=3$
. Since flasque sheaves do not have higher cohomology, we see that for every open subset
$i=3$
. Since flasque sheaves do not have higher cohomology, we see that for every open subset
![]() $U\subset X$
we have a short exact sequence of abelian groups
$U\subset X$
we have a short exact sequence of abelian groups
 $\mathsf{M}_{1}(U){\hookrightarrow}\mathsf{M}_{2}(U){\twoheadrightarrow}\mathsf{M}_{3}(U)$
. In particular, we obtain a commutative diagram with exact rows
$\mathsf{M}_{1}(U){\hookrightarrow}\mathsf{M}_{2}(U){\twoheadrightarrow}\mathsf{M}_{3}(U)$
. In particular, we obtain a commutative diagram with exact rows

with the left and right vertical arrows being surjective. The snake lemma or a simple diagram chase reveal that the vertical map in the middle also has to be surjective. This proves that
![]() $\mathsf{M}_{2}$
is a flasque sheaf.◻
$\mathsf{M}_{2}$
is a flasque sheaf.◻
Definition 2.5. We denote the exact category, given by the extension-closed full subcategory of
 $\mathsf{Mod}(\mathsf{A})$
consisting of modules whose underlying sheaf is flasque, by
$\mathsf{Mod}(\mathsf{A})$
consisting of modules whose underlying sheaf is flasque, by
 $\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A})$
.
$\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A})$
.
We refer the reader to [Reference KellerKel96] and [Reference BühlerBüh10] for the notion of derived categories of exact categories. We also emphasise that we use the notation
![]() $\mathsf{D}(-)$
to denote the stable
$\mathsf{D}(-)$
to denote the stable
![]() $\infty$
-category obtained by applying the dg-nerve construction of [Reference LurieLur, § 1.3.1] to the dg-category of [Reference KellerKel96]. We will also consider similarly constructed stable
$\infty$
-category obtained by applying the dg-nerve construction of [Reference LurieLur, § 1.3.1] to the dg-category of [Reference KellerKel96]. We will also consider similarly constructed stable
![]() $\infty$
-categories
$\infty$
-categories
![]() $\mathsf{D}^{+}$
,
$\mathsf{D}^{+}$
,
![]() $\mathsf{D}^{-}$
and
$\mathsf{D}^{-}$
and
![]() $\mathsf{D}^{b}$
, corresponding to complexes which are bounded below, bounded above and bounded, respectively.
$\mathsf{D}^{b}$
, corresponding to complexes which are bounded below, bounded above and bounded, respectively.
It is important to emphasise that for a substantial part of this text we will not need to delve deeply into the theory of stable
![]() $\infty$
-categories. The homotopy category of a stable
$\infty$
-categories. The homotopy category of a stable
![]() $\infty$
-category is naturally triangulated. To check that a functor
$\infty$
-category is naturally triangulated. To check that a functor
 $F:\mathsf{C}\rightarrow \mathsf{D}$
is fully faithful, essentially surjective, or an equivalence, it suffices to prove the same statement for its homotopy category (that is a classical triangulated category). This is essentially a consequence of the Whitehead lemma. Distinguished triangles
$F:\mathsf{C}\rightarrow \mathsf{D}$
is fully faithful, essentially surjective, or an equivalence, it suffices to prove the same statement for its homotopy category (that is a classical triangulated category). This is essentially a consequence of the Whitehead lemma. Distinguished triangles
 $X\rightarrow Y\rightarrow Z\rightarrow \unicode[STIX]{x1D6F4}X$
correspond to so-called bi-cartesian squares
$X\rightarrow Y\rightarrow Z\rightarrow \unicode[STIX]{x1D6F4}X$
correspond to so-called bi-cartesian squares

that is, commutative diagrams which are cartesian and co-cartesian. A functor
![]() $\mathsf{C}\rightarrow \mathsf{D}$
between stable
$\mathsf{C}\rightarrow \mathsf{D}$
between stable
![]() $\infty$
-categories is called exact, if it preserves bi-cartesian squares. In particular, this is the case if and only if the induced functor
$\infty$
-categories is called exact, if it preserves bi-cartesian squares. In particular, this is the case if and only if the induced functor
 $\mathsf{Ho}(\mathsf{C})\rightarrow \mathsf{Ho}(\mathsf{D})$
is exact in the sense of triangulated categories. The embedding
$\mathsf{Ho}(\mathsf{C})\rightarrow \mathsf{Ho}(\mathsf{D})$
is exact in the sense of triangulated categories. The embedding
 $\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}){\hookrightarrow}\mathsf{Mod}(\mathsf{A})$
induces an exact functor of derived categories.
$\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}){\hookrightarrow}\mathsf{Mod}(\mathsf{A})$
induces an exact functor of derived categories.
Lemma 2.6. The canonical functor
 $\mathsf{D}^{+}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))\rightarrow \mathsf{D}^{+}(\mathsf{A})$
, induced by the exact functor
$\mathsf{D}^{+}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))\rightarrow \mathsf{D}^{+}(\mathsf{A})$
, induced by the exact functor
 $\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}){\hookrightarrow}\mathsf{Mod}(\mathsf{A})$
, is fully faithful.
$\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}){\hookrightarrow}\mathsf{Mod}(\mathsf{A})$
, is fully faithful.
Proof. According to a theorem of Keller [Reference KellerKel96, Theorem 12.1] it suffices to check that every short exact sequence of
![]() $\mathsf{A}$
-modules
$\mathsf{A}$
-modules
 $\mathsf{M}_{1}{\hookrightarrow}\mathsf{M}_{2}{\twoheadrightarrow}\mathsf{M}_{3}$
with
$\mathsf{M}_{1}{\hookrightarrow}\mathsf{M}_{2}{\twoheadrightarrow}\mathsf{M}_{3}$
with
![]() $\mathsf{M}_{1}$
flasque fits into a commutative diagram with exact rows
$\mathsf{M}_{1}$
flasque fits into a commutative diagram with exact rows

with
![]() $\mathsf{M}_{2}^{\prime }$
and
$\mathsf{M}_{2}^{\prime }$
and
![]() $\mathsf{M}_{3}^{\prime }$
flasque. To produce this diagram, we recall that every
$\mathsf{M}_{3}^{\prime }$
flasque. To produce this diagram, we recall that every
![]() $\mathsf{A}$
-module
$\mathsf{A}$
-module
![]() $\mathsf{M}$
can be embedded into a flasque
$\mathsf{M}$
can be embedded into a flasque
![]() $\mathsf{A}$
-module. Indeed, the sheaf of discontinuous sections, that is,
$\mathsf{A}$
-module. Indeed, the sheaf of discontinuous sections, that is,
 $\mathsf{M}^{\text{dc}}(U)=\prod _{x\in U}\mathsf{M}_{x}$
provides such an embedding. Let
$\mathsf{M}^{\text{dc}}(U)=\prod _{x\in U}\mathsf{M}_{x}$
provides such an embedding. Let
 $\mathsf{M}_{2}{\hookrightarrow}\mathsf{M}_{2}^{\prime }$
be an embedding of
$\mathsf{M}_{2}{\hookrightarrow}\mathsf{M}_{2}^{\prime }$
be an embedding of
![]() $\mathsf{M}_{2}$
into a flasque
$\mathsf{M}_{2}$
into a flasque
![]() $\mathsf{A}$
-module. Then, the quotient
$\mathsf{A}$
-module. Then, the quotient
 $\mathsf{M}_{3}^{\prime }=\mathsf{M}_{2}^{\prime }/\mathsf{M}_{1}$
is also flasque by Lemma 2.3.◻
$\mathsf{M}_{3}^{\prime }=\mathsf{M}_{2}^{\prime }/\mathsf{M}_{1}$
is also flasque by Lemma 2.3.◻
2.1.2 Flasque sheaves of algebras
In this subsection we ponder over what can be said about quasi-coherent sheaves of
![]() $\mathsf{A}$
-modules, if the sheaves of algebras
$\mathsf{A}$
-modules, if the sheaves of algebras
![]() $\mathsf{A}$
itself is known to be flasque. Recall that an
$\mathsf{A}$
itself is known to be flasque. Recall that an
![]() $\mathsf{A}$
-module
$\mathsf{A}$
-module
![]() $\mathsf{M}$
is quasi-coherent, if every point
$\mathsf{M}$
is quasi-coherent, if every point
![]() $x\in X$
has a neighbourhood
$x\in X$
has a neighbourhood
![]() $U\subset X$
, such that the restriction
$U\subset X$
, such that the restriction
![]() $\mathsf{M}|_{U}$
can be represented as a cokernel of a morphism
$\mathsf{M}|_{U}$
can be represented as a cokernel of a morphism
 $\mathsf{A}^{\oplus J}|_{U}\rightarrow \mathsf{A}^{\oplus I}|_{U}$
of free
$\mathsf{A}^{\oplus J}|_{U}\rightarrow \mathsf{A}^{\oplus I}|_{U}$
of free
![]() $\mathsf{A}$
-modules.
$\mathsf{A}$
-modules.
Remark 2.7. For a general sheaf of algebras
![]() $\mathsf{A}$
the category
$\mathsf{A}$
the category
 $\mathsf{QCoh}(\mathsf{A})$
of quasi-coherent
$\mathsf{QCoh}(\mathsf{A})$
of quasi-coherent
![]() $\mathsf{A}$
-modules is in general not closed under taking kernels in the abelian category of
$\mathsf{A}$
-modules is in general not closed under taking kernels in the abelian category of
![]() $\mathsf{A}$
-modules
$\mathsf{A}$
-modules
 $\mathsf{Mod}(\mathsf{A})$
. In particular, one does not expect
$\mathsf{Mod}(\mathsf{A})$
. In particular, one does not expect
 $\mathsf{QCoh}(\mathsf{A})$
to be abelian in general. If the restriction maps
$\mathsf{QCoh}(\mathsf{A})$
to be abelian in general. If the restriction maps
 $\mathsf{A}(V)\rightarrow \mathsf{A}(U)$
for
$\mathsf{A}(V)\rightarrow \mathsf{A}(U)$
for
![]() $U\subset V$
belonging to a specific subbase for the topology are known to be flat,
$U\subset V$
belonging to a specific subbase for the topology are known to be flat,
 $\mathsf{QCoh}(\mathsf{A})$
can be shown to be abelian. This assumption is too strong for the sheaves of algebras we care about in this article.
$\mathsf{QCoh}(\mathsf{A})$
can be shown to be abelian. This assumption is too strong for the sheaves of algebras we care about in this article.
We see from Lemma 2.1 that every locally finite free or locally finite projective sheaf of
![]() $\mathsf{A}$
-modules is flasque (where
$\mathsf{A}$
-modules is flasque (where
![]() $\mathsf{A}$
is itself a flasque sheaf of algebras). In general, one cannot expect every quasi-coherent sheaf of
$\mathsf{A}$
is itself a flasque sheaf of algebras). In general, one cannot expect every quasi-coherent sheaf of
![]() $\mathsf{A}$
-modules to be flasque. However, we will see in the next subsection that there are certain flasque sheaves of algebras for which this is true.
$\mathsf{A}$
-modules to be flasque. However, we will see in the next subsection that there are certain flasque sheaves of algebras for which this is true.
Lemma 2.8. Let
![]() $\mathsf{A}$
be a sheaf of algebras on
$\mathsf{A}$
be a sheaf of algebras on
![]() $X$
, such that every free
$X$
, such that every free
![]() $\mathsf{A}$
-module is flasque. We denote by
$\mathsf{A}$
-module is flasque. We denote by
![]() $\mathsf{P}(\mathsf{A})$
the exact category given by the idempotent completion of free
$\mathsf{P}(\mathsf{A})$
the exact category given by the idempotent completion of free
![]() $\mathsf{A}$
-modules, and refer to its objects as projective
$\mathsf{A}$
-modules, and refer to its objects as projective
![]() $\mathsf{A}$
-modules. The functor
$\mathsf{A}$
-modules. The functor
 $\mathsf{D}^{-}(\mathsf{P}(\mathsf{A})){\hookrightarrow}\mathsf{D}^{-}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))$
, induced by the inclusion
$\mathsf{D}^{-}(\mathsf{P}(\mathsf{A})){\hookrightarrow}\mathsf{D}^{-}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))$
, induced by the inclusion
 $\mathsf{P}(\mathsf{A}){\hookrightarrow}\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A})$
, is fully faithful.
$\mathsf{P}(\mathsf{A}){\hookrightarrow}\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A})$
, is fully faithful.
Proof. We will apply the dual of the result in Keller [Reference KellerKel96, Theorem 12.1], by which it suffices to check that every short exact sequence of flasque
![]() $\mathsf{A}$
-modules
$\mathsf{A}$
-modules
 $\mathsf{M}_{1}{\hookrightarrow}\mathsf{M}_{2}{\twoheadrightarrow}\mathsf{M}_{3}$
with
$\mathsf{M}_{1}{\hookrightarrow}\mathsf{M}_{2}{\twoheadrightarrow}\mathsf{M}_{3}$
with
![]() $\mathsf{M}_{3}$
projective fits into a commutative diagram with exact rows
$\mathsf{M}_{3}$
projective fits into a commutative diagram with exact rows

with
![]() $\mathsf{M}_{1}^{\prime }$
and
$\mathsf{M}_{1}^{\prime }$
and
![]() $\mathsf{M}_{2}^{\prime }$
projective. Since
$\mathsf{M}_{2}^{\prime }$
projective. Since
 $\mathsf{M}_{2}\in \mathsf{Mod}_{\mathsf{fl}}(\mathsf{A})$
is flasque by assumption, there exists a surjection
$\mathsf{M}_{2}\in \mathsf{Mod}_{\mathsf{fl}}(\mathsf{A})$
is flasque by assumption, there exists a surjection
 $\mathsf{A}^{\oplus I}\rightarrow \mathsf{M}_{2}$
for some index set
$\mathsf{A}^{\oplus I}\rightarrow \mathsf{M}_{2}$
for some index set
![]() $I$
. Indeed, we can take
$I$
. Indeed, we can take
 $I=\{(U,s)|U\subset X\text{ open, }s\in \mathsf{M}_{2}(U)\}$
. Choosing an extension
$I=\{(U,s)|U\subset X\text{ open, }s\in \mathsf{M}_{2}(U)\}$
. Choosing an extension
 $t_{(U,s)}\in \mathsf{M}_{2}(X)$
, satisfying
$t_{(U,s)}\in \mathsf{M}_{2}(X)$
, satisfying
 $t_{(U,s)}|_{U}=s$
for every element of
$t_{(U,s)}|_{U}=s$
for every element of
![]() $I$
, we obtain a surjective morphism of
$I$
, we obtain a surjective morphism of
![]() $\mathsf{A}$
-module
$\mathsf{A}$
-module
 $\mathsf{A}^{\oplus I}\rightarrow \mathsf{M}_{2}$
.
$\mathsf{A}^{\oplus I}\rightarrow \mathsf{M}_{2}$
.
Let
 $\mathsf{M}_{2}^{\prime }=\mathsf{A}^{\oplus I}$
, and define
$\mathsf{M}_{2}^{\prime }=\mathsf{A}^{\oplus I}$
, and define
![]() $M_{1}^{\prime }$
to be the kernel of the composition
$M_{1}^{\prime }$
to be the kernel of the composition
 $\mathsf{M}_{2}^{\prime }\rightarrow \mathsf{M}_{2}\rightarrow \mathsf{M}_{3}$
. Since
$\mathsf{M}_{2}^{\prime }\rightarrow \mathsf{M}_{2}\rightarrow \mathsf{M}_{3}$
. Since
![]() $\mathsf{M}_{3}$
is a direct summand of a free
$\mathsf{M}_{3}$
is a direct summand of a free
![]() $\mathsf{A}$
-module, and
$\mathsf{A}$
-module, and
![]() $\mathsf{M}_{2}^{\prime }$
is flasque, there exists a splitting to this surjection. Therefore,
$\mathsf{M}_{2}^{\prime }$
is flasque, there exists a splitting to this surjection. Therefore,
![]() $\mathsf{M}_{1}^{\prime }$
belongs to
$\mathsf{M}_{1}^{\prime }$
belongs to
![]() $\mathsf{P}(\mathsf{A})$
, since it is a direct summand of
$\mathsf{P}(\mathsf{A})$
, since it is a direct summand of
![]() $\mathsf{M}_{2}^{\prime }$
. This concludes the proof.◻
$\mathsf{M}_{2}^{\prime }$
. This concludes the proof.◻
2.1.3 Definition of lâche sheaves of algebras
If
![]() $\mathsf{A}$
is a sheaf of algebras on a topological space, then there is a strengthening of the notion of
$\mathsf{A}$
is a sheaf of algebras on a topological space, then there is a strengthening of the notion of
![]() $\mathsf{A}$
being flasque.
$\mathsf{A}$
being flasque.
Definition 2.9. A sheaf of algebras
![]() $\mathsf{A}$
on
$\mathsf{A}$
on
![]() $X$
is called lâche if for every open subset
$X$
is called lâche if for every open subset
![]() $U\subset X$
and every map of free
$U\subset X$
and every map of free
![]() $\mathsf{A}_{U}$
-modules
$\mathsf{A}_{U}$
-modules
 $\mathsf{A}_{U}^{\oplus J}\xrightarrow[{}]{f}\mathsf{A}_{U}^{\oplus I}$
, the kernel
$\mathsf{A}_{U}^{\oplus J}\xrightarrow[{}]{f}\mathsf{A}_{U}^{\oplus I}$
, the kernel
![]() $\ker f$
is a flasque sheaf on
$\ker f$
is a flasque sheaf on
![]() $U$
.
$U$
.
To see that there are non-trivial lâche sheaves of algebras, we let
![]() $X$
be a topological space where every open subset is also closed in the following example.
$X$
be a topological space where every open subset is also closed in the following example.
Example 2.10. Let
![]() $X$
be a topological space, where every open subset is also closed. Then every sheaf of abelian groups
$X$
be a topological space, where every open subset is also closed. Then every sheaf of abelian groups
![]() ${\mathcal{F}}$
is flasque. If
${\mathcal{F}}$
is flasque. If
![]() $U\subset X$
is open, and
$U\subset X$
is open, and
 $s\in {\mathcal{F}}(U)$
, then using the sheaf property of
$s\in {\mathcal{F}}(U)$
, then using the sheaf property of
![]() ${\mathcal{F}}$
we see that there is a unique section
${\mathcal{F}}$
we see that there is a unique section
 $t\in {\mathcal{F}}(X)$
, such that
$t\in {\mathcal{F}}(X)$
, such that
![]() $t|_{U}=s$
and
$t|_{U}=s$
and
 $t|_{X\setminus U}=0$
. This is possible because
$t|_{X\setminus U}=0$
. This is possible because
![]() $X\setminus U$
is open by assumption. Hence, every sheaf of algebras on
$X\setminus U$
is open by assumption. Hence, every sheaf of algebras on
![]() $X$
is lâche.
$X$
is lâche.
The lemma below implies that for a lâche sheaf of algebras
![]() $\mathsf{A}$
, and a morphism
$\mathsf{A}$
, and a morphism
 $f:\mathsf{A}^{\oplus J}\rightarrow \mathsf{A}^{\oplus I}$
the sheaves
$f:\mathsf{A}^{\oplus J}\rightarrow \mathsf{A}^{\oplus I}$
the sheaves
![]() $\operatorname{im}f$
and
$\operatorname{im}f$
and
![]() $\operatorname{coker}f$
are flasque as well.
$\operatorname{coker}f$
are flasque as well.
Lemma 2.11. Let
 $V_{1}\xrightarrow[{}]{f}V_{2}$
be a morphism of flasque sheaves, such that
$V_{1}\xrightarrow[{}]{f}V_{2}$
be a morphism of flasque sheaves, such that
![]() $\ker f$
is flasque. Then, the sheaves
$\ker f$
is flasque. Then, the sheaves
![]() $\operatorname{im}f$
, and
$\operatorname{im}f$
, and
![]() $\operatorname{coker}f$
are flasque.
$\operatorname{coker}f$
are flasque.
Proof. We have a short exact sequence
 $\ker f{\hookrightarrow}V_{1}{\twoheadrightarrow}\operatorname{im}f$
, since the first two sheaves are flasque, so is the third (Lemma 2.3). The same argument applies to the short exact sequence
$\ker f{\hookrightarrow}V_{1}{\twoheadrightarrow}\operatorname{im}f$
, since the first two sheaves are flasque, so is the third (Lemma 2.3). The same argument applies to the short exact sequence
 $\operatorname{im}f{\hookrightarrow}V_{2}{\twoheadrightarrow}\operatorname{coker}f$
, and implies that
$\operatorname{im}f{\hookrightarrow}V_{2}{\twoheadrightarrow}\operatorname{coker}f$
, and implies that
![]() $\operatorname{coker}f$
is flasque.◻
$\operatorname{coker}f$
is flasque.◻
We can further generalise the assertion.
Lemma 2.12. Let
 $V_{1}\xrightarrow[{}]{f}V_{2}$
be a morphism of projective quasi-coherent
$V_{1}\xrightarrow[{}]{f}V_{2}$
be a morphism of projective quasi-coherent
![]() $\mathsf{A}$
-modules (that is, direct summands of free modules), where
$\mathsf{A}$
-modules (that is, direct summands of free modules), where
![]() $\mathsf{A}$
is lâche. Then the sheaves
$\mathsf{A}$
is lâche. Then the sheaves
![]() $\ker f$
,
$\ker f$
,
![]() $\operatorname{im}f$
and
$\operatorname{im}f$
and
![]() $\operatorname{coker}f$
are flasque.
$\operatorname{coker}f$
are flasque.
Proof. Since every projective quasi-coherent
![]() $\mathsf{A}$
-module is a direct summand of a free
$\mathsf{A}$
-module is a direct summand of a free
![]() $\mathsf{A}$
-module, there exist quasi-coherent
$\mathsf{A}$
-module, there exist quasi-coherent
![]() $\mathsf{A}$
-modules
$\mathsf{A}$
-modules
![]() $W_{1}$
and
$W_{1}$
and
![]() $W_{2}$
, such that
$W_{2}$
, such that
 $V_{i}\oplus W_{i}$
are free
$V_{i}\oplus W_{i}$
are free
![]() $\mathsf{A}$
-modules for
$\mathsf{A}$
-modules for
![]() $i=1,2$
. The induced map
$i=1,2$
. The induced map
 $$\begin{eqnarray}f\oplus \operatorname{id}:V_{1}\oplus (W_{1}\oplus W_{2}\oplus V_{1}\oplus V_{2})^{\oplus \mathbb{N}}\rightarrow V_{2}\oplus (W_{1}\oplus W_{2}\oplus V_{1}\oplus V_{2})^{\oplus \mathbb{N}}\end{eqnarray}$$
$$\begin{eqnarray}f\oplus \operatorname{id}:V_{1}\oplus (W_{1}\oplus W_{2}\oplus V_{1}\oplus V_{2})^{\oplus \mathbb{N}}\rightarrow V_{2}\oplus (W_{1}\oplus W_{2}\oplus V_{1}\oplus V_{2})^{\oplus \mathbb{N}}\end{eqnarray}$$
has the same kernel
 $\ker f\simeq \ker (f\oplus \operatorname{id})$
. However, the Eilenberg swindle
$\ker f\simeq \ker (f\oplus \operatorname{id})$
. However, the Eilenberg swindle
 $$\begin{eqnarray}(W_{1}\oplus W_{2}\oplus V_{1}\oplus V_{2})^{\oplus \mathbb{N}}\simeq (W_{1})^{i}\oplus (W_{2})^{j}\oplus (W_{1}\oplus W_{2}\oplus V_{1}\oplus V_{2})^{\oplus \mathbb{N}}\end{eqnarray}$$
$$\begin{eqnarray}(W_{1}\oplus W_{2}\oplus V_{1}\oplus V_{2})^{\oplus \mathbb{N}}\simeq (W_{1})^{i}\oplus (W_{2})^{j}\oplus (W_{1}\oplus W_{2}\oplus V_{1}\oplus V_{2})^{\oplus \mathbb{N}}\end{eqnarray}$$
allows us to see that the two sides are, in fact, free
![]() $\mathsf{A}$
-modules. Therefore, the defining property of lâche sheaf of algebras implies that
$\mathsf{A}$
-modules. Therefore, the defining property of lâche sheaf of algebras implies that
![]() $\ker f$
is flasque. Lemma 2.11 yields that
$\ker f$
is flasque. Lemma 2.11 yields that
![]() $\operatorname{im}f$
and
$\operatorname{im}f$
and
![]() $\operatorname{coker}f$
are flasque sheaves.◻
$\operatorname{coker}f$
are flasque sheaves.◻
The considerations above imply, in particular, that every quasi-coherent
![]() $\mathsf{A}$
-module of a lâche sheaf of algebras
$\mathsf{A}$
-module of a lâche sheaf of algebras
![]() $\mathsf{A}$
is flasque. However, we have to keep in mind that the category of quasi-coherent sheaves is not abelian in general, as we pointed out in Remark 2.7. We have the following corollary to Lemma 2.12.
$\mathsf{A}$
is flasque. However, we have to keep in mind that the category of quasi-coherent sheaves is not abelian in general, as we pointed out in Remark 2.7. We have the following corollary to Lemma 2.12.
Corollary 2.13. If
 $M^{\bullet }\in \mathsf{DMod}(\mathsf{A})$
is a complex of sheaves of
$M^{\bullet }\in \mathsf{DMod}(\mathsf{A})$
is a complex of sheaves of
![]() $\mathsf{A}$
-modules which is locally quasi-isomorphic to an object of
$\mathsf{A}$
-modules which is locally quasi-isomorphic to an object of
 $\mathsf{D}(\mathsf{P}(\mathsf{A}))$
, then its cohomology sheaves
$\mathsf{D}(\mathsf{P}(\mathsf{A}))$
, then its cohomology sheaves
![]() ${\mathcal{H}}^{i}(\mathsf{M}^{\bullet })$
are flasque.
${\mathcal{H}}^{i}(\mathsf{M}^{\bullet })$
are flasque.
Proof. We have seen in Lemma 2.1 that a sheaf is flasque if and only if it is locally flasque. Therefore, we may assume
 $M\in \mathsf{D}(\mathsf{P}(\mathsf{A}))$
. Let us choose an explicit presentation by a complex
$M\in \mathsf{D}(\mathsf{P}(\mathsf{A}))$
. Let us choose an explicit presentation by a complex
![]() $(V^{\bullet },d)$
, where each
$(V^{\bullet },d)$
, where each
![]() $V^{i}$
is a projective
$V^{i}$
is a projective
![]() $\mathsf{A}$
-module. We have
$\mathsf{A}$
-module. We have
 ${\mathcal{H}}^{i}(M)\simeq (\ker d^{i})/(\operatorname{im}d^{i-1})$
. By Lemma 2.12,
${\mathcal{H}}^{i}(M)\simeq (\ker d^{i})/(\operatorname{im}d^{i-1})$
. By Lemma 2.12,
![]() $\ker d^{i}$
and
$\ker d^{i}$
and
![]() $\operatorname{im}d^{i-1}$
are flasque. By Lemma 2.3, the quotient
$\operatorname{im}d^{i-1}$
are flasque. By Lemma 2.3, the quotient
![]() ${\mathcal{H}}^{i}(M)$
is flasque.◻
${\mathcal{H}}^{i}(M)$
is flasque.◻
2.1.4 A criterion for being lâche
In this subsection we observe that every sheaf of algebras
![]() $\mathsf{A}$
, which admits linear sections to the restriction maps
$\mathsf{A}$
, which admits linear sections to the restriction maps
 $\mathsf{A}(X)\rightarrow \mathsf{A}(U)$
, is in fact lâche. As a consequence, we obtain that the sheaf of adèles on a Noetherian scheme is lâche (Corollary 2.17).
$\mathsf{A}(X)\rightarrow \mathsf{A}(U)$
, is in fact lâche. As a consequence, we obtain that the sheaf of adèles on a Noetherian scheme is lâche (Corollary 2.17).
Definition 2.14. A sheaf of algebras
![]() $\mathsf{A}$
is called very flasque if for every open subset
$\mathsf{A}$
is called very flasque if for every open subset
![]() $U\subset X$
there exists an
$U\subset X$
there exists an
![]() $\mathsf{A}(X)$
-linear section
$\mathsf{A}(X)$
-linear section
![]() $\unicode[STIX]{x1D719}_{U}$
of the restriction map
$\unicode[STIX]{x1D719}_{U}$
of the restriction map
 $r_{U}:\mathsf{A}(X)\rightarrow \mathsf{A}(U)$
.
$r_{U}:\mathsf{A}(X)\rightarrow \mathsf{A}(U)$
.
Typically the section
![]() $\unicode[STIX]{x1D719}_{U}$
is given by a map which extends
$\unicode[STIX]{x1D719}_{U}$
is given by a map which extends
 $s\in \mathsf{A}(U)$
by 0 outside of
$s\in \mathsf{A}(U)$
by 0 outside of
![]() $U$
, as in the following example.
$U$
, as in the following example.
Example 2.15. Let
![]() $X$
be a topological space where every open subset is closed and
$X$
be a topological space where every open subset is closed and
![]() $\mathsf{A}$
an arbitrary sheaf of algebras, then
$\mathsf{A}$
an arbitrary sheaf of algebras, then
![]() $\mathsf{A}$
is very flasque.
$\mathsf{A}$
is very flasque.
Proof. For an open subset
![]() $U\subset X$
we have a map
$U\subset X$
we have a map
 $\unicode[STIX]{x1D719}:\mathsf{A}(U)\rightarrow \mathsf{A}(X)$
which sends
$\unicode[STIX]{x1D719}:\mathsf{A}(U)\rightarrow \mathsf{A}(X)$
which sends
 $s\in \mathsf{A}(U)$
to the unique section
$s\in \mathsf{A}(U)$
to the unique section
 $\widehat{s}\in \mathsf{A}(X)$
, such that
$\widehat{s}\in \mathsf{A}(X)$
, such that
![]() $\widehat{s}|_{U}=s$
, and
$\widehat{s}|_{U}=s$
, and
 $\widehat{s}|_{X\setminus U}=0$
. This definition makes sense because
$\widehat{s}|_{X\setminus U}=0$
. This definition makes sense because
![]() $\mathsf{A}$
is a sheaf, and
$\mathsf{A}$
is a sheaf, and
 $X=U\cup X\setminus U$
a disjoint open covering. Since this map is
$X=U\cup X\setminus U$
a disjoint open covering. Since this map is
![]() $\mathsf{A}(X)$
-linear, we have shown that
$\mathsf{A}(X)$
-linear, we have shown that
![]() $\mathsf{A}$
is very flasque.◻
$\mathsf{A}$
is very flasque.◻
In hindsight we have shown in Lemma 1.14 that for every quasi-coherent sheaf of algebras
![]() ${\mathcal{F}}$
on a Noetherian scheme
${\mathcal{F}}$
on a Noetherian scheme
![]() $X$
, the sheaves of algebras
$X$
, the sheaves of algebras
 $\mathbb{A}_{X,T}({\mathcal{F}})$
are very flasque. See also Corollary 2.17 below, where an important consequence of this observation is recorded.
$\mathbb{A}_{X,T}({\mathcal{F}})$
are very flasque. See also Corollary 2.17 below, where an important consequence of this observation is recorded.
The next lemma is the aforementioned criterion for a sheaf of algebras being lâche.
Lemma 2.16. A very flasque sheaf of algebras
![]() $\mathsf{A}$
is lâche.
$\mathsf{A}$
is lâche.
Proof. Let
 $f:\mathsf{A}_{V}^{\oplus J}\rightarrow \mathsf{A}_{V}^{\oplus I}$
be an
$f:\mathsf{A}_{V}^{\oplus J}\rightarrow \mathsf{A}_{V}^{\oplus I}$
be an
![]() $\mathsf{A}_{V}$
-linear map, where
$\mathsf{A}_{V}$
-linear map, where
![]() $V\subset X$
is open. We have to show that
$V\subset X$
is open. We have to show that
 $K=\ker f$
is a flasque sheaf on
$K=\ker f$
is a flasque sheaf on
![]() $V$
. For
$V$
. For
![]() $U\subset V$
open we have a commutative diagram
$U\subset V$
open we have a commutative diagram

with exact rows, because taking global sections is a left exact functor. However,
![]() $\mathsf{A}(V)$
-linearity of the section
$\mathsf{A}(V)$
-linearity of the section
 $r_{V}\circ \unicode[STIX]{x1D719}_{U}:\mathsf{A}(U)\rightarrow \mathsf{A}(V)$
implies that we have a commutative diagram
$r_{V}\circ \unicode[STIX]{x1D719}_{U}:\mathsf{A}(U)\rightarrow \mathsf{A}(V)$
implies that we have a commutative diagram

where the dashed arrow is provided by the universal property of kernels. The dashed arrow is therefore right-inverse to the restriction map
 $K(V)\rightarrow K(U)$
, and we conclude that
$K(V)\rightarrow K(U)$
, and we conclude that
 $K=\ker f$
is flasque.◻
$K=\ker f$
is flasque.◻
Corollary 2.17. For a Noetherian scheme
![]() $X$
and a quasi-coherent sheaf
$X$
and a quasi-coherent sheaf
![]() ${\mathcal{F}}$
of algebras, the sheaves of Beilinson–Parshin adèles
${\mathcal{F}}$
of algebras, the sheaves of Beilinson–Parshin adèles
 $\mathsf{A}_{X,T}({\mathcal{F}})$
are lâche sheaves of algebras.
$\mathsf{A}_{X,T}({\mathcal{F}})$
are lâche sheaves of algebras.
2.2 Perfect complexes
In this subsection we study the
![]() $\infty$
-category of perfect complexes of
$\infty$
-category of perfect complexes of
![]() $\mathsf{A}$
-modules. This is necessary since the classical category of quasi-coherent
$\mathsf{A}$
-modules. This is necessary since the classical category of quasi-coherent
![]() $\mathsf{A}$
-modules is not necessarily abelian (see Remark 2.7).
$\mathsf{A}$
-modules is not necessarily abelian (see Remark 2.7).
Definition 2.18. Let
![]() $\mathsf{P}(\mathsf{A})$
denote the exact category obtained as the idempotent completion of the exact category of free
$\mathsf{P}(\mathsf{A})$
denote the exact category obtained as the idempotent completion of the exact category of free
![]() $\mathsf{A}$
-modules. We denote by
$\mathsf{A}$
-modules. We denote by
![]() $\mathsf{D}^{-}(\mathsf{A})$
the
$\mathsf{D}^{-}(\mathsf{A})$
the
![]() $\infty$
-category corresponding to the full subcategory of
$\infty$
-category corresponding to the full subcategory of
 $\mathsf{D}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))$
given by complexes of flasque
$\mathsf{D}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))$
given by complexes of flasque
![]() $\mathsf{A}$
-modules
$\mathsf{A}$
-modules
![]() $\mathsf{M}^{\bullet }$
, which are locally equivalent to objects of
$\mathsf{M}^{\bullet }$
, which are locally equivalent to objects of
 $\mathsf{D}^{-}(\mathsf{P}(\mathsf{A}))$
. That is, there exists an open covering
$\mathsf{D}^{-}(\mathsf{P}(\mathsf{A}))$
. That is, there exists an open covering
 $X=\bigcup _{i\in I}U_{i}$
and complexes
$X=\bigcup _{i\in I}U_{i}$
and complexes
 $\mathsf{N}_{i}^{\bullet }\in \mathsf{D}^{-}(\mathsf{P}(\mathsf{A}|_{U_{i}}))$
such that we have equivalences
$\mathsf{N}_{i}^{\bullet }\in \mathsf{D}^{-}(\mathsf{P}(\mathsf{A}|_{U_{i}}))$
such that we have equivalences
 $\mathsf{N}_{i}^{\bullet }\simeq \mathsf{M}^{\bullet }|_{U_{i}}$
.
$\mathsf{N}_{i}^{\bullet }\simeq \mathsf{M}^{\bullet }|_{U_{i}}$
.
Recall that every exact functor between exact categories induces a functor between derived
![]() $\infty$
-categories.
$\infty$
-categories.
Lemma 2.19. Let
![]() $X$
be a quasi-compact topological space and
$X$
be a quasi-compact topological space and
![]() $\mathsf{A}$
a lâche sheaf of algebras on
$\mathsf{A}$
a lâche sheaf of algebras on
![]() $X$
. We denote by
$X$
. We denote by
 $R=\unicode[STIX]{x1D6E4}(\mathsf{A})$
the ring of global sections of
$R=\unicode[STIX]{x1D6E4}(\mathsf{A})$
the ring of global sections of
![]() $\mathsf{A}$
. The global sections functor
$\mathsf{A}$
. The global sections functor
 $\unicode[STIX]{x1D6E4}:\mathsf{D}^{-}(\mathsf{A})\rightarrow \mathsf{D}^{-}(R)$
, induced by the exact functor
$\unicode[STIX]{x1D6E4}:\mathsf{D}^{-}(\mathsf{A})\rightarrow \mathsf{D}^{-}(R)$
, induced by the exact functor
 $\unicode[STIX]{x1D6E4}:\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A})\rightarrow \mathsf{Mod}(R)$
, is conservative.
$\unicode[STIX]{x1D6E4}:\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A})\rightarrow \mathsf{Mod}(R)$
, is conservative.
Proof. Pick a complex
 $\mathsf{M}^{\bullet }=[\cdots \xrightarrow[{}]{d^{i-1}}M^{i}\xrightarrow[{}]{d^{i}}M^{i+1}\xrightarrow[{}]{d^{i+1}}\cdots \,]\in \mathsf{D}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))$
representing an object of
$\mathsf{M}^{\bullet }=[\cdots \xrightarrow[{}]{d^{i-1}}M^{i}\xrightarrow[{}]{d^{i}}M^{i+1}\xrightarrow[{}]{d^{i+1}}\cdots \,]\in \mathsf{D}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))$
representing an object of
![]() $\mathsf{D}^{-}(\mathsf{A})$
. By definition, we have
$\mathsf{D}^{-}(\mathsf{A})$
. By definition, we have
 $\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })=[\cdots \xrightarrow[{}]{\unicode[STIX]{x1D6E4}(d^{i-1})}\unicode[STIX]{x1D6E4}(M^{i})\xrightarrow[{}]{\unicode[STIX]{x1D6E4}(d^{i})}\unicode[STIX]{x1D6E4}(M^{i+1})\xrightarrow[{}]{\unicode[STIX]{x1D6E4}(d^{i+1})}\cdots \,]$
. We shall assume that
$\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })=[\cdots \xrightarrow[{}]{\unicode[STIX]{x1D6E4}(d^{i-1})}\unicode[STIX]{x1D6E4}(M^{i})\xrightarrow[{}]{\unicode[STIX]{x1D6E4}(d^{i})}\unicode[STIX]{x1D6E4}(M^{i+1})\xrightarrow[{}]{\unicode[STIX]{x1D6E4}(d^{i+1})}\cdots \,]$
. We shall assume that
![]() $\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })$
is acyclic, that is quasi-isomorphic to the 0-complex in
$\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })$
is acyclic, that is quasi-isomorphic to the 0-complex in
![]() $D^{-}(R)$
. To establish conservativity of the functor
$D^{-}(R)$
. To establish conservativity of the functor
![]() $\unicode[STIX]{x1D6E4}$
, we must show that
$\unicode[STIX]{x1D6E4}$
, we must show that
![]() $\mathsf{M}^{\bullet }$
is acyclic in
$\mathsf{M}^{\bullet }$
is acyclic in
 $D(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))$
.
$D(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))$
.
Since
![]() $X$
is assumed to be quasi-compact, and
$X$
is assumed to be quasi-compact, and
![]() $\mathsf{M}^{\bullet }$
locally quasi-isomorphic to an object of
$\mathsf{M}^{\bullet }$
locally quasi-isomorphic to an object of
 $D^{-}(\mathsf{P}(\mathsf{A}))$
, we see that there exists an
$D^{-}(\mathsf{P}(\mathsf{A}))$
, we see that there exists an
![]() $i\in \mathbb{Z}$
, such that the cohomology sheaves
$i\in \mathbb{Z}$
, such that the cohomology sheaves
 ${\mathcal{H}}^{j}(\mathsf{M}^{\bullet })=0$
vanish for
${\mathcal{H}}^{j}(\mathsf{M}^{\bullet })=0$
vanish for
![]() $j>i$
. We claim that for such an integer
$j>i$
. We claim that for such an integer
![]() $i$
we have that
$i$
we have that
 ${\mathcal{Z}}^{i}=\ker d^{i}$
has no higher cohomology. Indeed, by assumption the stupid truncation
${\mathcal{Z}}^{i}=\ker d^{i}$
has no higher cohomology. Indeed, by assumption the stupid truncation
 $\unicode[STIX]{x1D70E}_{i}\mathsf{M}^{\bullet }=[\cdots \rightarrow 0\rightarrow M^{i}\rightarrow M^{i+1}\rightarrow \cdots \,]$
is a flasque resolution of
$\unicode[STIX]{x1D70E}_{i}\mathsf{M}^{\bullet }=[\cdots \rightarrow 0\rightarrow M^{i}\rightarrow M^{i+1}\rightarrow \cdots \,]$
is a flasque resolution of
![]() ${\mathcal{Z}}^{i}[-i]$
, by assumption on the vanishing of
${\mathcal{Z}}^{i}[-i]$
, by assumption on the vanishing of
 ${\mathcal{H}}^{j}(\mathsf{M}^{\bullet })$
for
${\mathcal{H}}^{j}(\mathsf{M}^{\bullet })$
for
![]() $j>i$
. However, since
$j>i$
. However, since
![]() $\unicode[STIX]{x1D6E4}(M^{\bullet })$
has no cohomology in all degrees, we see that
$\unicode[STIX]{x1D6E4}(M^{\bullet })$
has no cohomology in all degrees, we see that
![]() $\unicode[STIX]{x1D70E}_{i}\mathsf{M}^{\bullet }$
has no cohomology in degrees
$\unicode[STIX]{x1D70E}_{i}\mathsf{M}^{\bullet }$
has no cohomology in degrees
![]() $j>i$
. This shows that
$j>i$
. This shows that
![]() ${\mathcal{Z}}^{i}$
has no higher cohomology.
${\mathcal{Z}}^{i}$
has no higher cohomology.
Let us denote the image sheaf of
![]() $d^{i-1}$
by
$d^{i-1}$
by
![]() ${\mathcal{B}}^{i}$
. It fits into a short exact sequence
${\mathcal{B}}^{i}$
. It fits into a short exact sequence
 ${\mathcal{B}}^{i}\rightarrow M^{i}{\twoheadrightarrow}{\mathcal{Z}}^{i}$
. Since
${\mathcal{B}}^{i}\rightarrow M^{i}{\twoheadrightarrow}{\mathcal{Z}}^{i}$
. Since
![]() $M^{i}$
and
$M^{i}$
and
![]() ${\mathcal{Z}}^{i}$
are acyclic, one sees from the associated long exact sequence that
${\mathcal{Z}}^{i}$
are acyclic, one sees from the associated long exact sequence that
![]() ${\mathcal{B}}^{i}$
has no higher cohomology if and only if
${\mathcal{B}}^{i}$
has no higher cohomology if and only if
 $\unicode[STIX]{x1D6E4}(M^{i})\xrightarrow[{}]{\unicode[STIX]{x1D6E4}(d^{i})}\unicode[STIX]{x1D6E4}({\mathcal{Z}}^{i})$
is surjective. By definition, the cokernel of this map equals
$\unicode[STIX]{x1D6E4}(M^{i})\xrightarrow[{}]{\unicode[STIX]{x1D6E4}(d^{i})}\unicode[STIX]{x1D6E4}({\mathcal{Z}}^{i})$
is surjective. By definition, the cokernel of this map equals
 $R^{i}\unicode[STIX]{x1D6E4}(M^{\bullet })=0$
. This is the case because
$R^{i}\unicode[STIX]{x1D6E4}(M^{\bullet })=0$
. This is the case because
![]() $\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })$
is acyclic, and therefore all its cohomology groups vanish.
$\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })$
is acyclic, and therefore all its cohomology groups vanish.
We have a commutative diagram

where the lower zigzag is a short exact sequence of sheaves without higher cohomology. Applying the functor
![]() $\unicode[STIX]{x1D6E4}$
(the short exact sequence is preserved by virtue of the fact that
$\unicode[STIX]{x1D6E4}$
(the short exact sequence is preserved by virtue of the fact that
![]() ${\mathcal{B}}^{i}$
has no higher cohomology) we obtain
${\mathcal{B}}^{i}$
has no higher cohomology) we obtain

Using again that
![]() $\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })$
has no non-zero cohomology groups, we see that
$\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })$
has no non-zero cohomology groups, we see that
![]() $\unicode[STIX]{x1D6E4}(d^{i-1})$
is surjective, and therefore so is the map
$\unicode[STIX]{x1D6E4}(d^{i-1})$
is surjective, and therefore so is the map
 $\unicode[STIX]{x1D6E4}({\mathcal{B}}^{i})\rightarrow \unicode[STIX]{x1D6E4}({\mathcal{Z}}^{i})$
. This implies
$\unicode[STIX]{x1D6E4}({\mathcal{B}}^{i})\rightarrow \unicode[STIX]{x1D6E4}({\mathcal{Z}}^{i})$
. This implies
 $\unicode[STIX]{x1D6E4}({\mathcal{H}}^{i})=0$
. However, we know from Corollary 2.13 that the cohomology sheaves of
$\unicode[STIX]{x1D6E4}({\mathcal{H}}^{i})=0$
. However, we know from Corollary 2.13 that the cohomology sheaves of
![]() $\mathsf{M}^{\bullet }$
are locally flasque, and therefore flasque by Lemma 2.1. Since a flasque sheaf without non-zero global sections is the zero sheaf, we obtain
$\mathsf{M}^{\bullet }$
are locally flasque, and therefore flasque by Lemma 2.1. Since a flasque sheaf without non-zero global sections is the zero sheaf, we obtain
 ${\mathcal{H}}^{i}(\mathsf{M}^{\bullet })=0$
. Continuing this process by downward induction, we obtain that all cohomology sheaves of
${\mathcal{H}}^{i}(\mathsf{M}^{\bullet })=0$
. Continuing this process by downward induction, we obtain that all cohomology sheaves of
![]() $\mathsf{M}^{\bullet }$
vanish.
$\mathsf{M}^{\bullet }$
vanish.
To conclude the proof we need to show that
![]() $\mathsf{M}^{\bullet }$
is acyclic in
$\mathsf{M}^{\bullet }$
is acyclic in
 $\mathsf{D}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))$
. By [Reference BühlerBüh10, Definition 10.1 and Remark 10.19] this is equivalent to the assertion that the sheaves
$\mathsf{D}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))$
. By [Reference BühlerBüh10, Definition 10.1 and Remark 10.19] this is equivalent to the assertion that the sheaves
![]() ${\mathcal{Z}}^{i}$
and
${\mathcal{Z}}^{i}$
and
![]() ${\mathcal{B}}^{i}$
are flasque. Since sheaves are flasque if they are locally flasque by Lemma 2.1, it suffices to show that
${\mathcal{B}}^{i}$
are flasque. Since sheaves are flasque if they are locally flasque by Lemma 2.1, it suffices to show that
![]() $\mathsf{M}^{\bullet }$
is locally acyclic.
$\mathsf{M}^{\bullet }$
is locally acyclic.
By assumption we can cover
![]() $X$
by open subsets
$X$
by open subsets
![]() $U$
, such that
$U$
, such that
![]() $\mathsf{M}^{\bullet }|_{U}$
is quasi-isomorphic to a complex of projective
$\mathsf{M}^{\bullet }|_{U}$
is quasi-isomorphic to a complex of projective
![]() $\mathsf{A}$
-modules
$\mathsf{A}$
-modules
 $P^{\bullet }\in \mathsf{D}^{-}(\mathsf{P}(\mathsf{A}|_{U}))$
. In particular, we see that
$P^{\bullet }\in \mathsf{D}^{-}(\mathsf{P}(\mathsf{A}|_{U}))$
. In particular, we see that
![]() $P^{\bullet }$
is a complex of projective sheaves of
$P^{\bullet }$
is a complex of projective sheaves of
![]() $\mathsf{A}|_{U}$
-modules
$\mathsf{A}|_{U}$
-modules
 $[\cdots \rightarrow P^{i-1}\rightarrow P^{i}\rightarrow 0\rightarrow \cdots \,]$
, such that
$[\cdots \rightarrow P^{i-1}\rightarrow P^{i}\rightarrow 0\rightarrow \cdots \,]$
, such that
 ${\mathcal{H}}^{k}(P^{\bullet })=0$
for all
${\mathcal{H}}^{k}(P^{\bullet })=0$
for all
![]() $k\in \mathbb{Z}$
. This implies the existence of a factorisation
$k\in \mathbb{Z}$
. This implies the existence of a factorisation

where the lower zigzags are short exact sequences. Since
 $P^{i}=Q^{i}$
is projective, we see that the first sequence splits, and therefore
$P^{i}=Q^{i}$
is projective, we see that the first sequence splits, and therefore
![]() $Q^{i-1}$
is projective too. Continuing by downward induction, we see that
$Q^{i-1}$
is projective too. Continuing by downward induction, we see that
![]() $Q^{j}$
is projective for all integers
$Q^{j}$
is projective for all integers
![]() $j$
, and therefore
$j$
, and therefore
![]() $P^{\bullet }\simeq 0$
in
$P^{\bullet }\simeq 0$
in
 $\mathsf{D}(\mathsf{P}(\mathsf{A}|_{U}))$
. We have seen in Lemma 2.8 that the functor
$\mathsf{D}(\mathsf{P}(\mathsf{A}|_{U}))$
. We have seen in Lemma 2.8 that the functor
 $\mathsf{D}^{-}(\mathsf{P}(\mathsf{A}|_{U})){\hookrightarrow}\mathsf{D}^{-}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}|_{U}))$
is fully faithful. This shows that
$\mathsf{D}^{-}(\mathsf{P}(\mathsf{A}|_{U})){\hookrightarrow}\mathsf{D}^{-}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}|_{U}))$
is fully faithful. This shows that
 $\mathsf{M}^{\bullet }|_{U}\simeq 0$
is acyclic, and therefore that the restriction of the sheaves
$\mathsf{M}^{\bullet }|_{U}\simeq 0$
is acyclic, and therefore that the restriction of the sheaves
![]() ${\mathcal{B}}^{i}$
and
${\mathcal{B}}^{i}$
and
![]() ${\mathcal{Z}}^{i}$
to
${\mathcal{Z}}^{i}$
to
![]() $U$
are flasque. As discussed above this concludes the proof that
$U$
are flasque. As discussed above this concludes the proof that
![]() $\mathsf{M}^{\bullet }$
is acyclic in
$\mathsf{M}^{\bullet }$
is acyclic in
 $\mathsf{D}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))$
.◻
$\mathsf{D}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))$
.◻
We also have a localisation functor.
Definition 2.20. For
![]() $\mathsf{A}$
a lâche sheaf of algebras on
$\mathsf{A}$
a lâche sheaf of algebras on
![]() $X$
, we have an exact functor between exact categories
$X$
, we have an exact functor between exact categories
 $-\otimes _{R}\mathsf{A}:\mathsf{P}(R)\rightarrow \mathsf{P}(\mathsf{A}){\hookrightarrow}\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A})$
. The induced exact functor between derived
$-\otimes _{R}\mathsf{A}:\mathsf{P}(R)\rightarrow \mathsf{P}(\mathsf{A}){\hookrightarrow}\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A})$
. The induced exact functor between derived
![]() $\infty$
-categories will be denoted by
$\infty$
-categories will be denoted by
 $$\begin{eqnarray}\mathsf{Loc}:\mathsf{D}^{-}(R)\rightarrow \mathsf{D}^{-}(\mathsf{A}).\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Loc}:\mathsf{D}^{-}(R)\rightarrow \mathsf{D}^{-}(\mathsf{A}).\end{eqnarray}$$
Proposition 2.21. If
![]() $X$
is quasi-compact and
$X$
is quasi-compact and
![]() $\mathsf{A}$
is lâche, then
$\mathsf{A}$
is lâche, then
 $\unicode[STIX]{x1D6E4}:\mathsf{D}^{-}(\mathsf{A})\rightarrow \mathsf{D}^{-}(R)$
is an equivalence of
$\unicode[STIX]{x1D6E4}:\mathsf{D}^{-}(\mathsf{A})\rightarrow \mathsf{D}^{-}(R)$
is an equivalence of
![]() $\infty$
-categories, with inverse equivalence
$\infty$
-categories, with inverse equivalence
![]() $\mathsf{Loc}$
.
$\mathsf{Loc}$
.
Proof. There is a commutative triangle

of exact functors, inducing a natural equivalence of functors
 $\operatorname{id}_{\mathsf{D}^{-}(\mathsf{A})}\simeq \mathsf{Loc}\circ \unicode[STIX]{x1D6E4}$
. We claim that we also have an equivalence
$\operatorname{id}_{\mathsf{D}^{-}(\mathsf{A})}\simeq \mathsf{Loc}\circ \unicode[STIX]{x1D6E4}$
. We claim that we also have an equivalence
 $\unicode[STIX]{x1D6E4}\circ \mathsf{Loc}\simeq \operatorname{id}_{\mathsf{D}^{-}(R)}$
. To see this, consider
$\unicode[STIX]{x1D6E4}\circ \mathsf{Loc}\simeq \operatorname{id}_{\mathsf{D}^{-}(R)}$
. To see this, consider
 $\mathsf{M}^{\bullet }\in \mathsf{D}^{-}(\mathsf{A})$
. We will show that
$\mathsf{M}^{\bullet }\in \mathsf{D}^{-}(\mathsf{A})$
. We will show that
![]() $\mathsf{M}^{\bullet }$
belongs to the essential image of
$\mathsf{M}^{\bullet }$
belongs to the essential image of
![]() $\mathsf{Loc}$
. Let
$\mathsf{Loc}$
. Let
 $g:P^{\bullet }\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })$
be a projective replacement of
$g:P^{\bullet }\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })$
be a projective replacement of
![]() $\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })$
, given by an actual morphism between chain complexes in
$\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })$
, given by an actual morphism between chain complexes in
 $\mathsf{Mod}(R)$
. By the adjunction between
$\mathsf{Mod}(R)$
. By the adjunction between
![]() $-\otimes _{R}\,\mathsf{A}$
and
$-\otimes _{R}\,\mathsf{A}$
and
![]() $\unicode[STIX]{x1D6E4}$
, this yields a morphism
$\unicode[STIX]{x1D6E4}$
, this yields a morphism
 $f:\mathsf{Loc}(P^{\bullet })\simeq \mathsf{Loc}(\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet }))\rightarrow \mathsf{M}^{\bullet }$
in
$f:\mathsf{Loc}(P^{\bullet })\simeq \mathsf{Loc}(\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet }))\rightarrow \mathsf{M}^{\bullet }$
in
![]() $\mathsf{D}^{-}(\mathsf{A})$
. Since
$\mathsf{D}^{-}(\mathsf{A})$
. Since
 $\unicode[STIX]{x1D6E4}(f)=g$
is a quasi-isomorphism, and
$\unicode[STIX]{x1D6E4}(f)=g$
is a quasi-isomorphism, and
![]() $\unicode[STIX]{x1D6E4}$
is conservative by Lemma 2.19, we see that
$\unicode[STIX]{x1D6E4}$
is conservative by Lemma 2.19, we see that
![]() $f$
is an equivalence. This implies that every
$f$
is an equivalence. This implies that every
 $\mathsf{M}^{\bullet }\in \mathsf{D}^{-}(\mathsf{A})$
is in fact equivalent to an object of
$\mathsf{M}^{\bullet }\in \mathsf{D}^{-}(\mathsf{A})$
is in fact equivalent to an object of
 $\mathsf{D}^{-}(\mathsf{P}(\mathsf{A}))$
. Therefore, we have a natural equivalence
$\mathsf{D}^{-}(\mathsf{P}(\mathsf{A}))$
. Therefore, we have a natural equivalence
 $\mathsf{Loc}\circ \unicode[STIX]{x1D6E4}\simeq \operatorname{id}_{\mathsf{D}^{-}(\mathsf{A})}$
as a consequence of the commutative diagram
$\mathsf{Loc}\circ \unicode[STIX]{x1D6E4}\simeq \operatorname{id}_{\mathsf{D}^{-}(\mathsf{A})}$
as a consequence of the commutative diagram

of exact functors, and Lemma 2.8, which asserted
 $\mathsf{D}^{-}(\mathsf{P}(\mathsf{A})){\hookrightarrow}\mathsf{D}^{-}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))$
.◻
$\mathsf{D}^{-}(\mathsf{P}(\mathsf{A})){\hookrightarrow}\mathsf{D}^{-}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A}))$
.◻
Corollary 2.22. The functor
 $\unicode[STIX]{x1D6E4}:\mathsf{D}^{-}(\mathsf{A})\rightarrow \mathsf{D}^{-}(R)$
can be promoted to a symmetric monoidal equivalence of symmetric monoidal
$\unicode[STIX]{x1D6E4}:\mathsf{D}^{-}(\mathsf{A})\rightarrow \mathsf{D}^{-}(R)$
can be promoted to a symmetric monoidal equivalence of symmetric monoidal
![]() $\infty$
-categories.
$\infty$
-categories.
Proof. The functor
![]() $\mathsf{Loc}$
lifts to a symmetric monoidal functor, since
$\mathsf{Loc}$
lifts to a symmetric monoidal functor, since
![]() $-\otimes _{R}\mathsf{A}$
is a symmetric monoidal functor
$-\otimes _{R}\mathsf{A}$
is a symmetric monoidal functor
 $P(R)\rightarrow P(\mathsf{A})$
. Therefore, also the inverse functor
$P(R)\rightarrow P(\mathsf{A})$
. Therefore, also the inverse functor
![]() $\unicode[STIX]{x1D6E4}$
can be canonically lifted to a symmetric monoidal functor (see [Reference LurieLur, Remark 2.1.3.8] applied to the special case of the operad
$\unicode[STIX]{x1D6E4}$
can be canonically lifted to a symmetric monoidal functor (see [Reference LurieLur, Remark 2.1.3.8] applied to the special case of the operad
 ${\mathcal{O}}^{\otimes }=N(\mathsf{Fin}_{\ast })$
, as explained in [Reference LurieLur] in the paragraph preceding the cited remark).◻
${\mathcal{O}}^{\otimes }=N(\mathsf{Fin}_{\ast })$
, as explained in [Reference LurieLur] in the paragraph preceding the cited remark).◻
Corollary 2.23. The functor
![]() $\unicode[STIX]{x1D6E4}$
restricts to a symmetric monoidal equivalence of symmetric monoidal stable
$\unicode[STIX]{x1D6E4}$
restricts to a symmetric monoidal equivalence of symmetric monoidal stable
![]() $\infty$
-categories
$\infty$
-categories
 $$\begin{eqnarray}\mathsf{Perf}(\mathsf{A})_{\otimes }\rightarrow \mathsf{Perf}(R)_{\otimes },\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Perf}(\mathsf{A})_{\otimes }\rightarrow \mathsf{Perf}(R)_{\otimes },\end{eqnarray}$$
with inverse
![]() $\mathsf{Loc}$
.
$\mathsf{Loc}$
.
Proof. This follows from the equivalence
 $\mathsf{D}^{-}(\mathsf{A})_{\otimes }\simeq \mathsf{D}^{-}(R)_{\otimes }$
once we have shown that the mutually inverse functors
$\mathsf{D}^{-}(\mathsf{A})_{\otimes }\simeq \mathsf{D}^{-}(R)_{\otimes }$
once we have shown that the mutually inverse functors
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $\mathsf{Loc}$
induce functors
$\mathsf{Loc}$
induce functors
 $\unicode[STIX]{x1D6E4}:\mathsf{Perf}(\mathsf{A})\rightarrow \mathsf{Perf}(R)$
and
$\unicode[STIX]{x1D6E4}:\mathsf{Perf}(\mathsf{A})\rightarrow \mathsf{Perf}(R)$
and
 $\mathsf{Loc}:\mathsf{Perf}(R)\rightarrow \mathsf{Perf}(A)$
. Since
$\mathsf{Loc}:\mathsf{Perf}(R)\rightarrow \mathsf{Perf}(A)$
. Since
![]() $\mathsf{Loc}$
is induced by
$\mathsf{Loc}$
is induced by
![]() $-\otimes _{R}A$
it is clear that
$-\otimes _{R}A$
it is clear that
![]() $\mathsf{Loc}$
sends perfect complexes to perfect complexes.
$\mathsf{Loc}$
sends perfect complexes to perfect complexes.
To show that
![]() $\unicode[STIX]{x1D6E4}$
preserves perfect complexes, one uses that they are dualisable in
$\unicode[STIX]{x1D6E4}$
preserves perfect complexes, one uses that they are dualisable in
 $\mathsf{D}^{-}(\mathsf{A})_{\otimes }$
. The details are as follows. We have shown in Lemma 2.6 that the functor
$\mathsf{D}^{-}(\mathsf{A})_{\otimes }$
. The details are as follows. We have shown in Lemma 2.6 that the functor
 $$\begin{eqnarray}\mathsf{D}^{+}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A})){\hookrightarrow}\mathsf{DMod}^{+}(\mathsf{A})\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{D}^{+}(\mathsf{Mod}_{\mathsf{fl}}(\mathsf{A})){\hookrightarrow}\mathsf{DMod}^{+}(\mathsf{A})\end{eqnarray}$$
is fully faithful. In particular, let
 $\mathsf{M}^{\bullet }\in \mathsf{Perf}(\mathsf{A})\subset \mathsf{DMod}(\mathsf{A})$
be a chain complex, which is locally equivalent to bounded complexes of projective
$\mathsf{M}^{\bullet }\in \mathsf{Perf}(\mathsf{A})\subset \mathsf{DMod}(\mathsf{A})$
be a chain complex, which is locally equivalent to bounded complexes of projective
![]() $\mathsf{A}$
-modules. Since
$\mathsf{A}$
-modules. Since
![]() $X$
is quasi-compact, every perfect complex is automatically bounded, and therefore admits a bounded below resolution by flasque
$X$
is quasi-compact, every perfect complex is automatically bounded, and therefore admits a bounded below resolution by flasque
![]() $\mathsf{A}$
-modules. Therefore,
$\mathsf{A}$
-modules. Therefore,
 $\mathsf{M}^{\bullet }\in \mathsf{D}^{-}(\mathsf{A})$
. Moreover,
$\mathsf{M}^{\bullet }\in \mathsf{D}^{-}(\mathsf{A})$
. Moreover,
![]() $(\mathsf{M}^{\bullet })^{\vee }$
also belongs to
$(\mathsf{M}^{\bullet })^{\vee }$
also belongs to
![]() $\mathsf{D}^{-}(\mathsf{A})$
, and
$\mathsf{D}^{-}(\mathsf{A})$
, and
![]() $\mathsf{M}^{\bullet }$
is dualisable in
$\mathsf{M}^{\bullet }$
is dualisable in
![]() $\mathsf{D}^{-}(\mathsf{A})$
. Since
$\mathsf{D}^{-}(\mathsf{A})$
. Since
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $\mathsf{Loc}$
are symmetric monoidal functors, they preserve dualisable objects. We conclude that
$\mathsf{Loc}$
are symmetric monoidal functors, they preserve dualisable objects. We conclude that
![]() $\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })$
is a dualisable object in
$\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })$
is a dualisable object in
![]() $\mathsf{D}^{-}(R)$
. However, all dualisable objects in
$\mathsf{D}^{-}(R)$
. However, all dualisable objects in
![]() $D(R)$
are known to be perfect complexes (see [Reference Elmendorf, Kriz, Mandell and MayEKMM07, Theorem III.7.9]), hence we have
$D(R)$
are known to be perfect complexes (see [Reference Elmendorf, Kriz, Mandell and MayEKMM07, Theorem III.7.9]), hence we have
 $\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })\in \mathsf{Perf}(R)$
.◻
$\unicode[STIX]{x1D6E4}(\mathsf{M}^{\bullet })\in \mathsf{Perf}(R)$
.◻
We do not know whether an analogue of Corollary 2.23 holds for flasque sheaves of algebras. However, for a locally compact (and therefore in particular Hausdorff) topological space
![]() $X$
, it was shown by Illusie in [Reference Grothendieck and IllusieGI71, Exposé II, Proposition 2.3.2] that a similar result holds for perfect complexes over soft sheaves of algebras.
$X$
, it was shown by Illusie in [Reference Grothendieck and IllusieGI71, Exposé II, Proposition 2.3.2] that a similar result holds for perfect complexes over soft sheaves of algebras.
3 Adelic descent for perfect complexes and maps to stacks
This section is concerned with proving the adelic descent theorem, and exploring its consequences. We refer the reader to Definition 1.4 for Beilinson’s sheaf of adèles.
Theorem 3.1 (Adelic descent).
For every Noetherian scheme
![]() $X$
we have an equivalence of symmetric monoidal
$X$
we have an equivalence of symmetric monoidal
![]() $\infty$
-categories
$\infty$
-categories
 $$\begin{eqnarray}\mathsf{Perf}(X)_{\otimes }\simeq |\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })_{\otimes }|,\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Perf}(X)_{\otimes }\simeq |\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })_{\otimes }|,\end{eqnarray}$$
where
![]() $\mathbb{A}_{X}^{\bullet }$
denotes the co-simplicial ring of Beilinson–Parshin adèles, and
$\mathbb{A}_{X}^{\bullet }$
denotes the co-simplicial ring of Beilinson–Parshin adèles, and
 $|\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })_{\otimes }|$
denotes the totalisation of the co-simplicial object
$|\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })_{\otimes }|$
denotes the totalisation of the co-simplicial object
 $\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })_{\otimes }$
in the
$\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })_{\otimes }$
in the
![]() $\infty$
-category of small monoidal stable
$\infty$
-category of small monoidal stable
![]() $\infty$
-categories.
$\infty$
-categories.
Let
![]() $S^{\bullet }$
be a co-simplicial ring. Applying the functor
$S^{\bullet }$
be a co-simplicial ring. Applying the functor
 $\mathsf{Perf}:\mathsf{Rng}\rightarrow \infty \text{-}\mathsf{Cat}$
, assigning to a ring
$\mathsf{Perf}:\mathsf{Rng}\rightarrow \infty \text{-}\mathsf{Cat}$
, assigning to a ring
![]() $R$
the stable
$R$
the stable
![]() $\infty$
-category of perfect
$\infty$
-category of perfect
![]() $R$
-complexes, we obtain a co-simplicial object in stable
$R$
-complexes, we obtain a co-simplicial object in stable
![]() $\infty$
-categories,
$\infty$
-categories,
 $\mathsf{Perf}(S^{\bullet })$
. The objects of the limit
$\mathsf{Perf}(S^{\bullet })$
. The objects of the limit
![]() $\infty$
-category
$\infty$
-category
 $|\mathsf{Perf}(S^{\bullet })|$
will also be referred to as cartesian co-simplicial perfect
$|\mathsf{Perf}(S^{\bullet })|$
will also be referred to as cartesian co-simplicial perfect
![]() $S^{\bullet }$
-complexes. This formulation is inspired by a co-simplicial formulation of Grothendieck’s faithfully flat descent theory. We briefly review this viewpoint to motivate the following considerations. More details can be found in [Sta, Tag 039Y]. For
$S^{\bullet }$
-complexes. This formulation is inspired by a co-simplicial formulation of Grothendieck’s faithfully flat descent theory. We briefly review this viewpoint to motivate the following considerations. More details can be found in [Sta, Tag 039Y]. For
![]() $R\rightarrow S$
a ring homomorphism, we may define a co-simplicial ring
$R\rightarrow S$
a ring homomorphism, we may define a co-simplicial ring
![]() $S^{\bullet }$
, where
$S^{\bullet }$
, where
![]() $S^{k}$
can be identified with tensoring
$S^{k}$
can be identified with tensoring
![]() $S$
with itself
$S$
with itself
![]() $(k+1)$
-times;
$(k+1)$
-times;
 $S^{k}=S\otimes _{R}\cdots \otimes _{R}S$
. A co-simplicial
$S^{k}=S\otimes _{R}\cdots \otimes _{R}S$
. A co-simplicial
![]() $S^{\bullet }$
-module consists of a co-simplicial
$S^{\bullet }$
-module consists of a co-simplicial
![]() $R$
-module
$R$
-module
![]() $M^{\bullet }$
, such that
$M^{\bullet }$
, such that
![]() $M^{k}$
is an
$M^{k}$
is an
![]() $S^{k}$
-module, compatibly with the co-simplicial structure on
$S^{k}$
-module, compatibly with the co-simplicial structure on
![]() $M^{\bullet }$
and
$M^{\bullet }$
and
![]() $S^{\bullet }$
. We say that
$S^{\bullet }$
. We say that
![]() $M^{\bullet }$
is a cartesian
$M^{\bullet }$
is a cartesian
![]() $S^{\bullet }$
-module, if for every
$S^{\bullet }$
-module, if for every
 $[k]\rightarrow [n]$
the induced map
$[k]\rightarrow [n]$
the induced map
 $M^{k}\otimes _{R^{k}}R^{n}\rightarrow M^{n}$
is an isomorphism of
$M^{k}\otimes _{R^{k}}R^{n}\rightarrow M^{n}$
is an isomorphism of
![]() $R^{n}$
-modules. Classical descent theory asserts that for
$R^{n}$
-modules. Classical descent theory asserts that for
![]() $R\rightarrow S$
faithfully flat, we have an equivalence of categories between
$R\rightarrow S$
faithfully flat, we have an equivalence of categories between
![]() $R$
-modules and cartesian
$R$
-modules and cartesian
![]() $S^{\bullet }$
-modules.
$S^{\bullet }$
-modules.
3.1 Proof of the adelic descent theorem
The adelic descent Theorem 3.1 follows from an analogous assertion for sheaves of symmetric monoidal
![]() $\infty$
-categories.
$\infty$
-categories.
Proposition 3.2. For every Noetherian scheme
![]() $X$
we have an equivalence of sheaves of symmetric monoidal
$X$
we have an equivalence of sheaves of symmetric monoidal
![]() $\infty$
-categories
$\infty$
-categories
 $$\begin{eqnarray}-\otimes \mathsf{A}_{X}^{\bullet }:\mathsf{Perf}({\mathcal{O}}_{X})_{\otimes }\simeq |\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })_{\otimes }|,\end{eqnarray}$$
$$\begin{eqnarray}-\otimes \mathsf{A}_{X}^{\bullet }:\mathsf{Perf}({\mathcal{O}}_{X})_{\otimes }\simeq |\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })_{\otimes }|,\end{eqnarray}$$
where
![]() $\mathsf{A}_{X}^{\bullet }$
denotes the co-simplicial sheaf of algebras of Beilinson–Parshin adèles.
$\mathsf{A}_{X}^{\bullet }$
denotes the co-simplicial sheaf of algebras of Beilinson–Parshin adèles.
In order to deduce the aforementioned theorem from this result, one takes global section: we have seen in Corollary 2.23 that taking global sections is a symmetric monoidal equivalence. More details can be found in § 3.1.5.
3.1.1 The adelic realisation functor
Our proof requires an
![]() $\infty$
-category which is closed under small colimits and contains
$\infty$
-category which is closed under small colimits and contains
 $|\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|$
. This is necessary to apply Lurie’s adjoint functor Theorem A.3.
$|\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|$
. This is necessary to apply Lurie’s adjoint functor Theorem A.3.
Definition 3.3. For a sheaf of algebras
![]() $\mathsf{A}$
on a topological space
$\mathsf{A}$
on a topological space
![]() $X$
, we define
$X$
, we define
 $\mathsf{QC}(\mathsf{A})=\mathsf{Ind}\mathsf{Perf}(\mathsf{A})$
. Let
$\mathsf{QC}(\mathsf{A})=\mathsf{Ind}\mathsf{Perf}(\mathsf{A})$
. Let
![]() $X$
be a Noetherian scheme, we define the category
$X$
be a Noetherian scheme, we define the category
 $|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
to be the geometric realisation of the co-simplicial object
$|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
to be the geometric realisation of the co-simplicial object
 $\mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
in symmetric monoidal
$\mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
in symmetric monoidal
![]() $\infty$
-categories.
$\infty$
-categories.
This definition is optimal for the sheaves of algebras considered in this paper but can diverge from more standard definitions in pathological cases, as the following remark shows.
Remark 3.4. If
![]() $X$
is a scheme which is quasi-compact and quasi-separated, then
$X$
is a scheme which is quasi-compact and quasi-separated, then
 $\mathsf{QC}({\mathcal{O}}_{X})$
is equivalent to the full subcategory of
$\mathsf{QC}({\mathcal{O}}_{X})$
is equivalent to the full subcategory of
 $\mathsf{DMod}({\mathcal{O}}_{X})$
of complexes of sheaves with quasi-coherent cohomology (see [Reference NeemanNee96, Proposition 2.5] for the quasi-compact and separated case, and [Reference Bondal and Van den BerghBV03, Theorem 3.1.1] for the general statement). However, if these technical assumptions are not satisfied, this is no longer the case. For a general scheme
$\mathsf{DMod}({\mathcal{O}}_{X})$
of complexes of sheaves with quasi-coherent cohomology (see [Reference NeemanNee96, Proposition 2.5] for the quasi-compact and separated case, and [Reference Bondal and Van den BerghBV03, Theorem 3.1.1] for the general statement). However, if these technical assumptions are not satisfied, this is no longer the case. For a general scheme
![]() $X$
we will denote by
$X$
we will denote by
![]() $\mathsf{QC}(X)$
the full subcategory of
$\mathsf{QC}(X)$
the full subcategory of
 $\mathsf{DMod}({\mathcal{O}}_{X})$
of complex of
$\mathsf{DMod}({\mathcal{O}}_{X})$
of complex of
![]() ${\mathcal{O}}_{X}$
-modules with quasi-coherent cohomology.
${\mathcal{O}}_{X}$
-modules with quasi-coherent cohomology.
Next we define the adelic realisation functor.
Definition 3.5. The adelic realisation functor
 $\mathsf{Perf}({\mathcal{O}}_{X})_{\otimes }\rightarrow \mathsf{Perf}(\mathsf{A}_{X}^{\bullet })_{\otimes }$
is given by tensoring a perfect complex of
$\mathsf{Perf}({\mathcal{O}}_{X})_{\otimes }\rightarrow \mathsf{Perf}(\mathsf{A}_{X}^{\bullet })_{\otimes }$
is given by tensoring a perfect complex of
![]() ${\mathcal{O}}_{X}$
-modules with the co-simplicial sheaf of rings
${\mathcal{O}}_{X}$
-modules with the co-simplicial sheaf of rings
![]() $\mathsf{A}_{X}^{\bullet }$
. Since
$\mathsf{A}_{X}^{\bullet }$
. Since
 $\mathsf{QC}({\mathcal{O}}_{X})_{\otimes }=\mathsf{Ind}\mathsf{Perf}({\mathcal{O}}_{X})_{\otimes }$
, and analogously
$\mathsf{QC}({\mathcal{O}}_{X})_{\otimes }=\mathsf{Ind}\mathsf{Perf}({\mathcal{O}}_{X})_{\otimes }$
, and analogously
 $\mathsf{QC}(\mathsf{A}_{X}^{k})=\mathsf{Ind}\mathsf{Perf}(\mathsf{A}_{X}^{k})$
for every
$\mathsf{QC}(\mathsf{A}_{X}^{k})=\mathsf{Ind}\mathsf{Perf}(\mathsf{A}_{X}^{k})$
for every
![]() $[k]\in \unicode[STIX]{x1D6E5}$
we obtain an extension of this functor
$[k]\in \unicode[STIX]{x1D6E5}$
we obtain an extension of this functor
 $$\begin{eqnarray}-\otimes \mathsf{A}_{X}^{\bullet }:\mathsf{QC}({\mathcal{O}}_{X})_{\otimes }\rightarrow \mathsf{QC}(\mathsf{A}_{X}^{\bullet })_{\otimes }.\end{eqnarray}$$
$$\begin{eqnarray}-\otimes \mathsf{A}_{X}^{\bullet }:\mathsf{QC}({\mathcal{O}}_{X})_{\otimes }\rightarrow \mathsf{QC}(\mathsf{A}_{X}^{\bullet })_{\otimes }.\end{eqnarray}$$
In light of Proposition 3.2 it is tempting to believe that the adelic descent functor
 $\mathsf{QC}({\mathcal{O}}_{X})\rightarrow |\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
is an equivalence. However, due to pathological behaviour of complexes of modules over infinite products of rings, we do not expect this to be true. The
$\mathsf{QC}({\mathcal{O}}_{X})\rightarrow |\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
is an equivalence. However, due to pathological behaviour of complexes of modules over infinite products of rings, we do not expect this to be true. The
![]() $\infty$
-category
$\infty$
-category
 $|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
is stable, and admits small colimits for formal reasons.
$|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
is stable, and admits small colimits for formal reasons.
Lemma 3.6. The
![]() $\infty$
-category
$\infty$
-category
 $|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
is stable, possesses a canonical symmetric monoidal structure, and is closed under small colimits. Moreover, it is presentable.
$|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
is stable, possesses a canonical symmetric monoidal structure, and is closed under small colimits. Moreover, it is presentable.
Proof. By definition,
 $|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
is the limit of a co-simplicial diagram of symmetric monoidal stable
$|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
is the limit of a co-simplicial diagram of symmetric monoidal stable
![]() $\infty$
-categories. Therefore, it is stable (see [Reference LurieLur, Proposition 1.1.4.6]) and symmetric monoidal itself.
$\infty$
-categories. Therefore, it is stable (see [Reference LurieLur, Proposition 1.1.4.6]) and symmetric monoidal itself.
The
![]() $\infty$
-categories
$\infty$
-categories
 $\mathsf{QC}(\mathsf{A}_{X}^{k})=\mathsf{Ind}\mathsf{Perf}(\mathsf{A}_{X}^{k})$
are presentable for each
$\mathsf{QC}(\mathsf{A}_{X}^{k})=\mathsf{Ind}\mathsf{Perf}(\mathsf{A}_{X}^{k})$
are presentable for each
![]() $k\in \mathbf{N}$
(see [Reference LurieLur07, Theorem 5.5.1.1(4)]). Since a limit of presentable
$k\in \mathbf{N}$
(see [Reference LurieLur07, Theorem 5.5.1.1(4)]). Since a limit of presentable
![]() $\infty$
-categories is again presentable [Reference LurieLur07, Proposition 5.5.3.13], we see that this is also the case for
$\infty$
-categories is again presentable [Reference LurieLur07, Proposition 5.5.3.13], we see that this is also the case for
 $|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
. Presentable
$|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
. Presentable
![]() $\infty$
-categories possess small colimits by [Reference LurieLur07, Definition 5.5.0.1].◻
$\infty$
-categories possess small colimits by [Reference LurieLur07, Definition 5.5.0.1].◻
We also know that this
![]() $\infty$
-category is locally small by Remark A.1.
$\infty$
-category is locally small by Remark A.1.
3.1.2 The right adjoint to adelic realisation
The adelic realisation functor preserves small coproducts. This follows from its definition using tensor products, and the description of mapping spaces in the
![]() $\infty$
-category
$\infty$
-category
 $|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
given in Lemma A.2. Since it is exact, it commutes with small colimits by virtue of Proposition A.4. Moreover, we know that
$|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
given in Lemma A.2. Since it is exact, it commutes with small colimits by virtue of Proposition A.4. Moreover, we know that
 $\mathsf{QC}(X)=\mathsf{Ind}\mathsf{Perf}(X)$
is presentable. By Lurie’s adjoint functor theorem (Theorem A.3) we see that there exists a right adjoint
$\mathsf{QC}(X)=\mathsf{Ind}\mathsf{Perf}(X)$
is presentable. By Lurie’s adjoint functor theorem (Theorem A.3) we see that there exists a right adjoint
 $\int _{X}:|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|\rightarrow \mathsf{QC}(X)$
.
$\int _{X}:|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|\rightarrow \mathsf{QC}(X)$
.
Definition 3.7. The right adjoint to the functor
 $-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }:\mathsf{QC}(X)\rightarrow |\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
will be denoted by
$-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }:\mathsf{QC}(X)\rightarrow |\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
will be denoted by
 $\int _{X}:|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|\rightarrow \mathsf{QC}(X)$
.
$\int _{X}:|\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|\rightarrow \mathsf{QC}(X)$
.
It is possible to give a more concrete definition of the functor
![]() $\int _{X}$
. For a discussion in terms of model categories we refer the reader to Toën–Vezzosi’s treatment [Reference Toën and VezzosiTV08, 1.2.12], which also inspired the notation
$\int _{X}$
. For a discussion in terms of model categories we refer the reader to Toën–Vezzosi’s treatment [Reference Toën and VezzosiTV08, 1.2.12], which also inspired the notation
![]() $\int$
. We will content ourselves with the following observation: by virtue of
$\int$
. We will content ourselves with the following observation: by virtue of
 $\mathsf{QC}(X)=\mathsf{Ind}\mathsf{Perf}(X)$
, we may view objects in
$\mathsf{QC}(X)=\mathsf{Ind}\mathsf{Perf}(X)$
, we may view objects in
![]() $\mathsf{QC}(X)$
as functors
$\mathsf{QC}(X)$
as functors
 $\mathsf{Perf}(X)^{\mathsf{op}}\rightarrow \infty \text{-}\mathsf{Gpd}$
, sending finite colimits in
$\mathsf{Perf}(X)^{\mathsf{op}}\rightarrow \infty \text{-}\mathsf{Gpd}$
, sending finite colimits in
 $\mathsf{Perf}(X)$
(that is, finite limits in
$\mathsf{Perf}(X)$
(that is, finite limits in
 $\mathsf{Perf}(X)^{\mathsf{op}}$
) to finite limits in
$\mathsf{Perf}(X)^{\mathsf{op}}$
) to finite limits in
![]() $\infty \text{-}\mathsf{Gpd}$
. The adjunction between
$\infty \text{-}\mathsf{Gpd}$
. The adjunction between
 $-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }$
and
$-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }$
and
![]() $\int _{X}$
implies that for
$\int _{X}$
implies that for
 $N^{\bullet }\in \mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
,
$N^{\bullet }\in \mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
,
![]() $\int _{X}N^{\bullet }$
is the functor
$\int _{X}N^{\bullet }$
is the functor
 $\mathsf{Perf}(X)^{\mathsf{op}}\rightarrow \infty \text{-}\mathsf{Gpd}$
, which informally is given by
$\mathsf{Perf}(X)^{\mathsf{op}}\rightarrow \infty \text{-}\mathsf{Gpd}$
, which informally is given by
 $$\begin{eqnarray}M\mapsto \mathsf{Map}_{\mathsf{A}_{X}^{\bullet }}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet },N^{\bullet }).\end{eqnarray}$$
$$\begin{eqnarray}M\mapsto \mathsf{Map}_{\mathsf{A}_{X}^{\bullet }}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet },N^{\bullet }).\end{eqnarray}$$
It follows from the proof of the adjoint functor theorem that
![]() $\int _{X}$
is equivalent to the functor
$\int _{X}$
is equivalent to the functor
 $$\begin{eqnarray}\mathsf{Map}_{\mathsf{A}_{X}^{\bullet }}(-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet },-):\mathsf{QC}(\mathsf{A}_{X})\times \mathsf{Perf}(X)^{\mathsf{op}}\rightarrow \infty \text{-}\mathsf{Gpd}.\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Map}_{\mathsf{A}_{X}^{\bullet }}(-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet },-):\mathsf{QC}(\mathsf{A}_{X})\times \mathsf{Perf}(X)^{\mathsf{op}}\rightarrow \infty \text{-}\mathsf{Gpd}.\end{eqnarray}$$
We record this for later use.
Lemma 3.8. With respect to the embedding
 $\mathsf{QC}(X)=\mathsf{Ind}\mathsf{Perf}(X)\subset \mathsf{Fun}(\mathsf{Perf}(X)^{\mathsf{op}},\infty \text{-}\mathsf{Gpd})$
, we have
$\mathsf{QC}(X)=\mathsf{Ind}\mathsf{Perf}(X)\subset \mathsf{Fun}(\mathsf{Perf}(X)^{\mathsf{op}},\infty \text{-}\mathsf{Gpd})$
, we have
 $\int _{X}\simeq \mathsf{Map}_{\mathsf{A}_{X}^{\bullet }}(-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet },-):\mathsf{QC}(\mathsf{A}_{X}^{\bullet })\times \mathsf{Perf}(X)^{\mathsf{op}}\rightarrow \infty \text{-}\mathsf{Gpd}$
.
$\int _{X}\simeq \mathsf{Map}_{\mathsf{A}_{X}^{\bullet }}(-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet },-):\mathsf{QC}(\mathsf{A}_{X}^{\bullet })\times \mathsf{Perf}(X)^{\mathsf{op}}\rightarrow \infty \text{-}\mathsf{Gpd}$
.
Another formal property of
![]() $\int _{X}$
of importance to us is its behaviour with respect to small colimits. We will give a heuristic justification that
$\int _{X}$
of importance to us is its behaviour with respect to small colimits. We will give a heuristic justification that
![]() $\int _{X}$
commutes with small colimits, before engaging with the formal argument. Since
$\int _{X}$
commutes with small colimits, before engaging with the formal argument. Since
![]() $|X|$
is a Noetherian topological space (that is, every open subset is quasi-compact), we have
$|X|$
is a Noetherian topological space (that is, every open subset is quasi-compact), we have
 $\mathsf{Perf}(\mathsf{A})\subset \mathsf{DMod}(\mathsf{A})^{c}$
, that is, every perfect complex of
$\mathsf{Perf}(\mathsf{A})\subset \mathsf{DMod}(\mathsf{A})^{c}$
, that is, every perfect complex of
![]() $\mathsf{A}$
-modules is compact. Thinking informally of
$\mathsf{A}$
-modules is compact. Thinking informally of
![]() $\int _{X}$
as a functor
$\int _{X}$
as a functor
 $\mathsf{QC}(\mathsf{A}_{X}^{\bullet })\times \mathsf{Perf}(X)^{\mathsf{op}}\rightarrow \infty \text{-}\mathsf{Gpd}$
, we see that
$\mathsf{QC}(\mathsf{A}_{X}^{\bullet })\times \mathsf{Perf}(X)^{\mathsf{op}}\rightarrow \infty \text{-}\mathsf{Gpd}$
, we see that
 $$\begin{eqnarray}{\int _{X}\bigoplus }_{i\in I}N_{i}^{\bullet }\simeq \bigoplus _{i\in I}\int _{X}N_{i}^{\bullet }:M\mapsto \mathsf{Hom}_{\mathsf{A}_{X}^{\bullet }}\biggl(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet },\bigoplus _{i\in I}N_{i}^{\bullet }\biggr)\simeq \bigoplus _{i\in I}\mathsf{Hom}_{\mathsf{A}_{X}^{\bullet }}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet },N_{i}^{\bullet }).\end{eqnarray}$$
$$\begin{eqnarray}{\int _{X}\bigoplus }_{i\in I}N_{i}^{\bullet }\simeq \bigoplus _{i\in I}\int _{X}N_{i}^{\bullet }:M\mapsto \mathsf{Hom}_{\mathsf{A}_{X}^{\bullet }}\biggl(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet },\bigoplus _{i\in I}N_{i}^{\bullet }\biggr)\simeq \bigoplus _{i\in I}\mathsf{Hom}_{\mathsf{A}_{X}^{\bullet }}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet },N_{i}^{\bullet }).\end{eqnarray}$$
The key observation of the heuristic reasoning above is that
 $-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }$
preserves compact objects. Therefore, we need a sufficient criterion for objects in
$-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }$
preserves compact objects. Therefore, we need a sufficient criterion for objects in
 $\mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
to be compact.
$\mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
to be compact.
Lemma 3.9. Let
 $M^{\bullet }\in \mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
be a cartesian co-simplicial
$M^{\bullet }\in \mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
be a cartesian co-simplicial
![]() $\mathsf{A}_{X}^{\bullet }$
-module. If
$\mathsf{A}_{X}^{\bullet }$
-module. If
 $M^{0}\in \mathsf{Perf}(\mathsf{A}_{X}^{0})\subset \mathsf{QC}(\mathsf{A}_{X}^{0})$
, then
$M^{0}\in \mathsf{Perf}(\mathsf{A}_{X}^{0})\subset \mathsf{QC}(\mathsf{A}_{X}^{0})$
, then
![]() $M^{\bullet }$
is compact in
$M^{\bullet }$
is compact in
 $\mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
.
$\mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
.
Proof. Let
![]() $(N_{i}^{\bullet })_{i\in I}$
be an arbitrary small family of objects in
$(N_{i}^{\bullet })_{i\in I}$
be an arbitrary small family of objects in
 $\mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
, and
$\mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
, and
 $f:M^{\bullet }\rightarrow \bigoplus _{i\in I}N_{i}^{\bullet }$
an arbitrary morphism. It suffices to show that there exists a finite subset
$f:M^{\bullet }\rightarrow \bigoplus _{i\in I}N_{i}^{\bullet }$
an arbitrary morphism. It suffices to show that there exists a finite subset
![]() $J\subset I$
, such that we have a factorisation
$J\subset I$
, such that we have a factorisation

To produce this factorisation, we will show that the space of commutative diagrams as drawn above is either empty or contractible. Since
 $\mathsf{Perf}(\mathsf{A}_{X}^{0})\subset \mathsf{QC}(\mathsf{A}_{X}^{0})^{c}$
, by virtue of the definition
$\mathsf{Perf}(\mathsf{A}_{X}^{0})\subset \mathsf{QC}(\mathsf{A}_{X}^{0})^{c}$
, by virtue of the definition
 $\mathsf{QC}(\mathsf{A}_{X}^{0})=\mathsf{Ind}\mathsf{Perf}(\mathsf{A}_{X}^{0})$
, we see that we have a finite subset
$\mathsf{QC}(\mathsf{A}_{X}^{0})=\mathsf{Ind}\mathsf{Perf}(\mathsf{A}_{X}^{0})$
, we see that we have a finite subset
![]() $J\subset I$
and a factorisation
$J\subset I$
and a factorisation
 $M^{0}\rightarrow \bigoplus _{i\in J}N_{i}^{0}\rightarrow \bigoplus _{i\in I}N_{i}^{0}$
. Since the modules
$M^{0}\rightarrow \bigoplus _{i\in J}N_{i}^{0}\rightarrow \bigoplus _{i\in I}N_{i}^{0}$
. Since the modules
![]() $M^{\bullet }$
and
$M^{\bullet }$
and
 $(N_{i}^{\bullet })_{i\in I}$
are cartesian, that is,
$(N_{i}^{\bullet })_{i\in I}$
are cartesian, that is,
 $M^{k}\simeq M^{0}\otimes _{\mathsf{A}_{X}^{0}}\mathsf{A}_{X}^{k}$
, we see that we have a factorisation
$M^{k}\simeq M^{0}\otimes _{\mathsf{A}_{X}^{0}}\mathsf{A}_{X}^{k}$
, we see that we have a factorisation
 $M^{k}\rightarrow \bigoplus _{i\in J}N_{i}^{k}\rightarrow \bigoplus _{i\in I}N_{i}^{k}$
for all co-simplicial levels
$M^{k}\rightarrow \bigoplus _{i\in J}N_{i}^{k}\rightarrow \bigoplus _{i\in I}N_{i}^{k}$
for all co-simplicial levels
![]() $k\geqslant 0$
.
$k\geqslant 0$
.
Consider the cartesian diagram of co-simplicial spaces

where
![]() $\mathsf{pt}^{\bullet }$
is the constant diagram, consisting levelwise of a single point, and the map
$\mathsf{pt}^{\bullet }$
is the constant diagram, consisting levelwise of a single point, and the map
 $\mathsf{pt}^{\bullet }\rightarrow \mathsf{Map}(M,\bigoplus _{i\in I}N_{i}^{\bullet })$
corresponds to the element
$\mathsf{pt}^{\bullet }\rightarrow \mathsf{Map}(M,\bigoplus _{i\in I}N_{i}^{\bullet })$
corresponds to the element
 $f\in |\mathsf{Map}(M,\bigoplus _{i\in I}N_{i}^{\bullet })|$
(where we used Lemma A.2). We know that the fibre
$f\in |\mathsf{Map}(M,\bigoplus _{i\in I}N_{i}^{\bullet })|$
(where we used Lemma A.2). We know that the fibre
 $X^{\bullet }\rightarrow \mathsf{pt}^{\bullet }$
is contractible: as we have remarked above, the space of factorisations through
$X^{\bullet }\rightarrow \mathsf{pt}^{\bullet }$
is contractible: as we have remarked above, the space of factorisations through
 $\bigoplus _{i\in J}N_{i}^{\bullet }\rightarrow \bigoplus _{i\in I}N_{i}^{\bullet }$
is either empty or contractible. We have shown that in the case of
$\bigoplus _{i\in J}N_{i}^{\bullet }\rightarrow \bigoplus _{i\in I}N_{i}^{\bullet }$
is either empty or contractible. We have shown that in the case of
![]() $f$
, a factorisation exists levelwise. Hence, we have a fibrewise equivalence
$f$
, a factorisation exists levelwise. Hence, we have a fibrewise equivalence
 $X^{\bullet }\rightarrow \mathsf{pt}^{\bullet }$
.
$X^{\bullet }\rightarrow \mathsf{pt}^{\bullet }$
.
Taking the limit of the co-simplicial diagram above, we obtain a cartesian diagram of spaces

which implies that there exists a unique factorisation as in (4). ◻
Lemma 3.10. The functor
![]() $\int _{X}$
commutes with small colimits.
$\int _{X}$
commutes with small colimits.
Proof. This follows from Lemma A.6, and the fact that
 $-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }$
preserves perfect complexes, that is, compact objects (by Lemma 3.9).◻
$-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }$
preserves perfect complexes, that is, compact objects (by Lemma 3.9).◻
The fact that
![]() $\int$
commutes with small colimits will be used in the proof of the following lemma.
$\int$
commutes with small colimits will be used in the proof of the following lemma.
Lemma 3.11 (Projection formula).
For every
 $M\in \mathsf{QC}(X)$
, and
$M\in \mathsf{QC}(X)$
, and
 $N^{\bullet }\in \mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
we have an equivalence in
$N^{\bullet }\in \mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
we have an equivalence in
![]() $\mathsf{QC}(X)$
$\mathsf{QC}(X)$
 $$\begin{eqnarray}\int _{X}M\otimes _{{\mathcal{O}}_{X}}N^{\bullet }\simeq M\otimes _{{\mathcal{O}}_{X}}\int _{X}N^{\bullet }.\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}M\otimes _{{\mathcal{O}}_{X}}N^{\bullet }\simeq M\otimes _{{\mathcal{O}}_{X}}\int _{X}N^{\bullet }.\end{eqnarray}$$
Proof. Since
![]() $\int _{X}$
commutes with small colimits by Lemma 3.10, we may assume without loss of generality that
$\int _{X}$
commutes with small colimits by Lemma 3.10, we may assume without loss of generality that
 $M\in \mathsf{Perf}(X)$
. In Lemma 3.8 we have seen that under the equivalence
$M\in \mathsf{Perf}(X)$
. In Lemma 3.8 we have seen that under the equivalence
 $\mathsf{QC}(X)=\mathsf{Ind}\mathsf{Perf}(X)$
, the functor
$\mathsf{QC}(X)=\mathsf{Ind}\mathsf{Perf}(X)$
, the functor
![]() $\int _{X}$
equivalent to
$\int _{X}$
equivalent to
 $\text{}\underline{\mathsf{Hom}}_{\mathsf{A}_{X}^{\bullet }}(-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet },-)$
, that is,
$\text{}\underline{\mathsf{Hom}}_{\mathsf{A}_{X}^{\bullet }}(-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet },-)$
, that is,
 $\int M\otimes N^{\bullet }$
is equivalent to the functor
$\int M\otimes N^{\bullet }$
is equivalent to the functor
 $(-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet })^{\vee }\otimes _{\mathsf{A}_{X}^{\bullet }}M\otimes _{{\mathcal{O}}_{X}}N^{\bullet }\simeq M\otimes _{{\mathcal{O}}_{X}}(-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet })^{\vee }\otimes _{\mathsf{A}_{X}^{\bullet }}N^{\bullet }$
. The right-hand side is equivalent to
$(-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet })^{\vee }\otimes _{\mathsf{A}_{X}^{\bullet }}M\otimes _{{\mathcal{O}}_{X}}N^{\bullet }\simeq M\otimes _{{\mathcal{O}}_{X}}(-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet })^{\vee }\otimes _{\mathsf{A}_{X}^{\bullet }}N^{\bullet }$
. The right-hand side is equivalent to
 $M\otimes _{{\mathcal{O}}_{X}}\int N^{\bullet }$
.◻
$M\otimes _{{\mathcal{O}}_{X}}\int N^{\bullet }$
.◻
Lemma 3.12. The unit
 $\operatorname{id}_{\mathsf{Perf}({\mathcal{O}}_{X})}\rightarrow \int (-\otimes \mathsf{A}_{X}^{\bullet })$
is an equivalence, that is, for every
$\operatorname{id}_{\mathsf{Perf}({\mathcal{O}}_{X})}\rightarrow \int (-\otimes \mathsf{A}_{X}^{\bullet })$
is an equivalence, that is, for every
 $M\in \mathsf{QC}({\mathcal{O}}_{X})$
we have
$M\in \mathsf{QC}({\mathcal{O}}_{X})$
we have
 $M\xrightarrow[{}]{\simeq }\int (M\otimes \mathsf{A}_{X}^{\bullet })$
.
$M\xrightarrow[{}]{\simeq }\int (M\otimes \mathsf{A}_{X}^{\bullet })$
.
Proof. This is a special case of Lemma 3.11, once we will have shown that
 $\int \mathsf{A}_{X}^{\bullet }\simeq {\mathcal{O}}_{X}$
. By definition, we have
$\int \mathsf{A}_{X}^{\bullet }\simeq {\mathcal{O}}_{X}$
. By definition, we have
 $\int _{X}\mathsf{A}_{X}^{\bullet }\simeq \text{}\underline{\mathsf{Hom}}_{\mathsf{A}_{X}^{\bullet }}(\mathsf{A}_{X}^{\bullet },\mathsf{A}_{X}^{\bullet })\simeq |\mathsf{A}_{X}^{\bullet }|$
, where the last equivalence uses the description of Hom-spaces in limits of
$\int _{X}\mathsf{A}_{X}^{\bullet }\simeq \text{}\underline{\mathsf{Hom}}_{\mathsf{A}_{X}^{\bullet }}(\mathsf{A}_{X}^{\bullet },\mathsf{A}_{X}^{\bullet })\simeq |\mathsf{A}_{X}^{\bullet }|$
, where the last equivalence uses the description of Hom-spaces in limits of
![]() $\infty$
-categories of Lemma A.2. By Theorem 1.16 the sheaf
$\infty$
-categories of Lemma A.2. By Theorem 1.16 the sheaf
![]() $|\mathsf{A}_{X}^{\bullet }|$
is canonically equivalent to
$|\mathsf{A}_{X}^{\bullet }|$
is canonically equivalent to
![]() ${\mathcal{O}}_{X}$
, by means of the augmentation
${\mathcal{O}}_{X}$
, by means of the augmentation
 ${\mathcal{O}}_{X}\rightarrow \mathsf{A}_{X}^{\bullet }$
.◻
${\mathcal{O}}_{X}\rightarrow \mathsf{A}_{X}^{\bullet }$
.◻
Consequently, we see that
 $-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }$
is fully faithful.
$-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }$
is fully faithful.
Corollary 3.13. The functor
 $-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }:\mathsf{QC}(X)=\mathsf{Ind}\mathsf{Perf}(X){\hookrightarrow}\mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
is fully faithful.
$-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }:\mathsf{QC}(X)=\mathsf{Ind}\mathsf{Perf}(X){\hookrightarrow}\mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
is fully faithful.
We will also use a minor variation of the notions introduced in the last two paragraphs. Let
![]() $|Z|$
be a closed subset of
$|Z|$
be a closed subset of
![]() $X$
, and denote by
$X$
, and denote by
![]() $\mathsf{A}_{X,|Z|}^{\bullet }$
the co-simplicial sheaf of algebras, given by setting
$\mathsf{A}_{X,|Z|}^{\bullet }$
the co-simplicial sheaf of algebras, given by setting
 $T_{\bullet }=|Z|_{\bullet }\subset |X|_{\bullet }$
in Proposition 1.7. There is a natural morphism of sheaves of algebras
$T_{\bullet }=|Z|_{\bullet }\subset |X|_{\bullet }$
in Proposition 1.7. There is a natural morphism of sheaves of algebras
 $\mathsf{A}_{X}^{\bullet }\rightarrow \mathsf{A}_{X,|Z|}^{\bullet }$
. We will also need to consider the full subcategory
$\mathsf{A}_{X}^{\bullet }\rightarrow \mathsf{A}_{X,|Z|}^{\bullet }$
. We will also need to consider the full subcategory
 $|\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|$
, consisting of objects, whose restriction (in the sense of sheaves) to
$|\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|$
, consisting of objects, whose restriction (in the sense of sheaves) to
 $|\mathsf{Perf}(\mathsf{A}_{X\setminus Z}^{\bullet })|$
is 0.
$|\mathsf{Perf}(\mathsf{A}_{X\setminus Z}^{\bullet })|$
is 0.
Lemma 3.14. The functor
 $-\otimes _{\mathsf{A}_{X}^{\bullet }}\mathsf{A}_{X,|Z|}^{\bullet }:|\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|{\hookrightarrow}|\mathsf{Perf}(\mathsf{A}_{X,|Z|}^{\bullet })|$
is fully faithful.
$-\otimes _{\mathsf{A}_{X}^{\bullet }}\mathsf{A}_{X,|Z|}^{\bullet }:|\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|{\hookrightarrow}|\mathsf{Perf}(\mathsf{A}_{X,|Z|}^{\bullet })|$
is fully faithful.
Proof. The morphism of co-simplicial rings
 $\mathsf{A}_{X}^{\bullet }\rightarrow \mathsf{A}_{X,|Z|}^{\bullet }$
has the property that it is levelwise the projection to a factor ring. That is, for each
$\mathsf{A}_{X}^{\bullet }\rightarrow \mathsf{A}_{X,|Z|}^{\bullet }$
has the property that it is levelwise the projection to a factor ring. That is, for each
![]() $n\geqslant 0$
, we have a decomposition
$n\geqslant 0$
, we have a decomposition
 $$\begin{eqnarray}\mathsf{A}_{X}^{n}\simeq \mathsf{A}_{X,|Z|_{n}}^{n}\times \mathsf{A}_{X,|X|_{n}\setminus |Z|_{n}}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{A}_{X}^{n}\simeq \mathsf{A}_{X,|Z|_{n}}^{n}\times \mathsf{A}_{X,|X|_{n}\setminus |Z|_{n}}^{n}.\end{eqnarray}$$
By induction one shows that for
 $M^{\bullet }\in |\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|,$
we have
$M^{\bullet }\in |\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|,$
we have
 $M^{n}\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|X|_{n}\setminus |Z|_{n}}^{n}\simeq 0$
.
$M^{n}\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|X|_{n}\setminus |Z|_{n}}^{n}\simeq 0$
.
This holds for
![]() $n=0$
by virtue of the assumption that
$n=0$
by virtue of the assumption that
 $M^{0}|_{X\setminus Z}\simeq 0$
. We assume by induction that it holds for
$M^{0}|_{X\setminus Z}\simeq 0$
. We assume by induction that it holds for
![]() $k\leqslant n$
, and we will show that
$k\leqslant n$
, and we will show that
 $M^{n+1}\otimes _{\mathsf{A}_{X}^{n+1}}\mathsf{A}_{X,|X|_{n+1}\setminus |Z|_{n+1}}^{n+1}\simeq 0$
. To see this, we observe that
$M^{n+1}\otimes _{\mathsf{A}_{X}^{n+1}}\mathsf{A}_{X,|X|_{n+1}\setminus |Z|_{n+1}}^{n+1}\simeq 0$
. To see this, we observe that
 $\mathsf{A}_{X,|X|_{n+1}\setminus |Z|_{n+1}}^{n+1}$
decomposes as a product
$\mathsf{A}_{X,|X|_{n+1}\setminus |Z|_{n+1}}^{n+1}$
decomposes as a product
 $\mathsf{A}_{X,T_{1}}^{n+1}\times \mathsf{A}_{X,T_{2}}^{n+1}$
. The subset
$\mathsf{A}_{X,T_{1}}^{n+1}\times \mathsf{A}_{X,T_{2}}^{n+1}$
. The subset
 $T_{1}\subset |X|_{n+1}$
consists of all chains
$T_{1}\subset |X|_{n+1}$
consists of all chains
 $(x_{0}\leqslant \cdots \leqslant x_{n+1})$
, with
$(x_{0}\leqslant \cdots \leqslant x_{n+1})$
, with
 $(x_{0}\leqslant \cdots \leqslant x_{n})\in |X|_{n}\setminus |Z|_{n}$
, and
$(x_{0}\leqslant \cdots \leqslant x_{n})\in |X|_{n}\setminus |Z|_{n}$
, and
 $x_{n+1}\in |Z|$
; and
$x_{n+1}\in |Z|$
; and
 $T_{2}\subset |X|_{n+1}$
consists of chains
$T_{2}\subset |X|_{n+1}$
consists of chains
 $(x_{0}\leqslant \cdots \leqslant x_{n+1})$
with
$(x_{0}\leqslant \cdots \leqslant x_{n+1})$
with
 $x_{n+1}\in |X|\setminus |Z|$
. We have equivalences
$x_{n+1}\in |X|\setminus |Z|$
. We have equivalences
 $$\begin{eqnarray}M^{n+1}\otimes _{\mathsf{A}_{X}^{n+1}}\mathsf{A}_{X,T_{1}}^{n+1}\simeq M^{n}\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|X|_{n}\setminus |Z|_{n}}^{n}\otimes _{\mathsf{A}_{X,|X|_{n}\setminus |Z|_{n}}^{n}}\mathsf{A}_{X,T_{1}}^{n+1}\simeq 0\end{eqnarray}$$
$$\begin{eqnarray}M^{n+1}\otimes _{\mathsf{A}_{X}^{n+1}}\mathsf{A}_{X,T_{1}}^{n+1}\simeq M^{n}\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|X|_{n}\setminus |Z|_{n}}^{n}\otimes _{\mathsf{A}_{X,|X|_{n}\setminus |Z|_{n}}^{n}}\mathsf{A}_{X,T_{1}}^{n+1}\simeq 0\end{eqnarray}$$
and
 $$\begin{eqnarray}M^{n+1}\otimes _{\mathsf{A}_{X}^{n+1}}\mathsf{A}_{X,T_{2}}^{n+1}\simeq M^{0}\otimes _{\mathsf{A}_{X}^{0}}\mathsf{A}_{X,|X|_{0}\setminus |Z|_{0}}^{0}\otimes _{\mathsf{A}_{X,|X|_{0}\setminus |Z|_{0}}^{0}}\mathsf{A}_{X,T_{2}}^{n+1}\simeq 0\end{eqnarray}$$
$$\begin{eqnarray}M^{n+1}\otimes _{\mathsf{A}_{X}^{n+1}}\mathsf{A}_{X,T_{2}}^{n+1}\simeq M^{0}\otimes _{\mathsf{A}_{X}^{0}}\mathsf{A}_{X,|X|_{0}\setminus |Z|_{0}}^{0}\otimes _{\mathsf{A}_{X,|X|_{0}\setminus |Z|_{0}}^{0}}\mathsf{A}_{X,T_{2}}^{n+1}\simeq 0\end{eqnarray}$$
by the induction hypothesis. This implies the vanishing assertion.
We have seen that for every
![]() $n\geqslant 0$
the functor
$n\geqslant 0$
the functor
 $-\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|Z|_{n}}^{n}$
is fully faithful, when restricted to the full subcategory of
$-\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|Z|_{n}}^{n}$
is fully faithful, when restricted to the full subcategory of
 $\mathsf{Perf}(\mathsf{A}_{X}^{n})$
, consisting of objects which are equivalent to 0, after tensoring with
$\mathsf{Perf}(\mathsf{A}_{X}^{n})$
, consisting of objects which are equivalent to 0, after tensoring with
 $-\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|X|_{n}\setminus |Z|_{n}}^{n}$
. That is, for two objects
$-\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|X|_{n}\setminus |Z|_{n}}^{n}$
. That is, for two objects
![]() $M^{\bullet }$
,
$M^{\bullet }$
,
![]() $N^{\bullet }$
in this category, we have an equivalence
$N^{\bullet }$
in this category, we have an equivalence
 $$\begin{eqnarray}\mathsf{Map}(M^{n},N^{n})\simeq \mathsf{Map}(M^{n}\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|Z|_{n}}^{n},N^{n}\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|Z|_{n}}^{n})\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Map}(M^{n},N^{n})\simeq \mathsf{Map}(M^{n}\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|Z|_{n}}^{n},N^{n}\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|Z|_{n}}^{n})\end{eqnarray}$$
for every
![]() $n\geqslant 0$
. This implies that
$n\geqslant 0$
. This implies that
 $$\begin{eqnarray}\underset{[n]\in \unicode[STIX]{x1D6E5}}{\mathsf{lim}}\mathsf{Map}(M^{n},N^{n})\rightarrow \underset{[n]\in \unicode[STIX]{x1D6E5}}{\mathsf{lim}}\mathsf{Map}(M^{n}\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|Z|_{n}}^{n},N^{n}\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|Z|_{n}}^{n})\end{eqnarray}$$
$$\begin{eqnarray}\underset{[n]\in \unicode[STIX]{x1D6E5}}{\mathsf{lim}}\mathsf{Map}(M^{n},N^{n})\rightarrow \underset{[n]\in \unicode[STIX]{x1D6E5}}{\mathsf{lim}}\mathsf{Map}(M^{n}\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|Z|_{n}}^{n},N^{n}\otimes _{\mathsf{A}_{X}^{n}}\mathsf{A}_{X,|Z|_{n}}^{n})\end{eqnarray}$$
is an equivalence too. Using Lemma A.2, we identify both sides with the mapping spaces in the limit
![]() $\infty$
-categories and see that the functor
$\infty$
-categories and see that the functor
 $$\begin{eqnarray}-\otimes _{\mathsf{A}_{X}^{\bullet }}\mathsf{A}_{X,|Z|}^{\bullet }:|\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|{\hookrightarrow}|\mathsf{Perf}(\mathsf{A}_{X,|Z|}^{\bullet })|\end{eqnarray}$$
$$\begin{eqnarray}-\otimes _{\mathsf{A}_{X}^{\bullet }}\mathsf{A}_{X,|Z|}^{\bullet }:|\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|{\hookrightarrow}|\mathsf{Perf}(\mathsf{A}_{X,|Z|}^{\bullet })|\end{eqnarray}$$
is fully faithful. ◻
Corollary 3.15. Let
 $\int _{X,|Z|}:\mathsf{QC}(\mathsf{A}_{X,|Z|}^{\bullet })\rightarrow \mathsf{QC}(X)$
be the right adjoint to
$\int _{X,|Z|}:\mathsf{QC}(\mathsf{A}_{X,|Z|}^{\bullet })\rightarrow \mathsf{QC}(X)$
be the right adjoint to
 $-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X,|Z|}^{\bullet }$
. We have an equivalence of functors
$-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X,|Z|}^{\bullet }$
. We have an equivalence of functors
 $$\begin{eqnarray}\int _{X,|Z|}~\circ ~(-\otimes _{\mathsf{A}_{X}^{\bullet }}\mathsf{A}_{X,|Z|}^{\bullet })\simeq \int _{X}:|\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|\rightarrow \mathsf{QC}(X).\end{eqnarray}$$
$$\begin{eqnarray}\int _{X,|Z|}~\circ ~(-\otimes _{\mathsf{A}_{X}^{\bullet }}\mathsf{A}_{X,|Z|}^{\bullet })\simeq \int _{X}:|\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|\rightarrow \mathsf{QC}(X).\end{eqnarray}$$
That is, for every
![]() $M^{\bullet }$
in
$M^{\bullet }$
in
 $|\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|$
, we have a natural equivalence
$|\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|$
, we have a natural equivalence
 $\int _{X}M^{\bullet }\simeq \int _{X,|Z|}(M^{\bullet }\otimes _{\mathsf{A}_{X}^{\bullet }}\mathsf{A}_{X,|Z|}^{\bullet })$
.
$\int _{X}M^{\bullet }\simeq \int _{X,|Z|}(M^{\bullet }\otimes _{\mathsf{A}_{X}^{\bullet }}\mathsf{A}_{X,|Z|}^{\bullet })$
.
Proof. For
![]() $M^{\bullet }$
in
$M^{\bullet }$
in
 $|\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|$
, we have
$|\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|$
, we have
 $\int _{X}M^{\bullet }\in \mathsf{QC}_{Z}(X)$
. Therefore, it suffices to consider only perfect complexes in
$\int _{X}M^{\bullet }\in \mathsf{QC}_{Z}(X)$
. Therefore, it suffices to consider only perfect complexes in
![]() $X$
with set-theoretic support
$X$
with set-theoretic support
![]() $|Z|$
. The right-hand side functor agrees with
$|Z|$
. The right-hand side functor agrees with
 $\mathsf{Map}(-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet },-):\mathsf{Perf}_{Z}(X)^{\mathsf{op}}\times |\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|\rightarrow \infty \text{-}\mathsf{Gpd}$
. By Lemma 3.14 it is equivalent to
$\mathsf{Map}(-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet },-):\mathsf{Perf}_{Z}(X)^{\mathsf{op}}\times |\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|\rightarrow \infty \text{-}\mathsf{Gpd}$
. By Lemma 3.14 it is equivalent to
 $\mathsf{Map}(-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X,|Z|}^{\bullet },-\otimes _{\mathsf{A}_{X}^{\bullet }}\mathsf{A}_{X,|Z|}^{\bullet })$
, hence to
$\mathsf{Map}(-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X,|Z|}^{\bullet },-\otimes _{\mathsf{A}_{X}^{\bullet }}\mathsf{A}_{X,|Z|}^{\bullet })$
, hence to
 $\int _{X,|Z|}\circ (-\otimes _{\mathsf{A}_{X}^{\bullet }}\,\mathsf{A}_{X,|Z|}^{\bullet })$
.◻
$\int _{X,|Z|}\circ (-\otimes _{\mathsf{A}_{X}^{\bullet }}\,\mathsf{A}_{X,|Z|}^{\bullet })$
.◻
3.1.3 Modules over product rings
This subsection relies on Bhatt’s treatment of perfect complexes over product rings
 $R=\prod _{i\in I}R_{i}$
, where
$R=\prod _{i\in I}R_{i}$
, where
![]() $I$
is a small set [Reference BhattBha16, § 7]. At first we review his characterisation of perfect
$I$
is a small set [Reference BhattBha16, § 7]. At first we review his characterisation of perfect
![]() $R$
-complexes. Let
$R$
-complexes. Let
 $\{M_{i}\}_{i\in I}$
be a family of perfect
$\{M_{i}\}_{i\in I}$
be a family of perfect
![]() $R_{i}$
-complexes. This requires a definition: we say that a family of complexes of
$R_{i}$
-complexes. This requires a definition: we say that a family of complexes of
![]() $R_{i}$
-modules
$R_{i}$
-modules
 $\{M_{i}\}_{i\in I}$
is globally bounded, if there exist two integers
$\{M_{i}\}_{i\in I}$
is globally bounded, if there exist two integers
 $m,n\in \mathbb{Z}$
, such that
$m,n\in \mathbb{Z}$
, such that
 $H^{j}(M_{i})\neq 0$
implies
$H^{j}(M_{i})\neq 0$
implies
 $m\leqslant j\leqslant n$
, for all
$m\leqslant j\leqslant n$
, for all
![]() $i\in I$
.
$i\in I$
.
Theorem 3.16 (Bhatt).
Let
![]() $I$
be a small set and
$I$
be a small set and
![]() $\{R_{i}\}_{i\in I}$
a small family of commutative rings. We denote the ring
$\{R_{i}\}_{i\in I}$
a small family of commutative rings. We denote the ring
 $\prod _{i\in I}R_{i}$
by
$\prod _{i\in I}R_{i}$
by
![]() $R$
. Then the functor
$R$
. Then the functor
 $\mathsf{Perf}(R)\rightarrow \prod _{i\in I}\mathsf{Perf}(R_{i})$
induced by tensoring along the projection maps
$\mathsf{Perf}(R)\rightarrow \prod _{i\in I}\mathsf{Perf}(R_{i})$
induced by tensoring along the projection maps
 $p_{i}:R\rightarrow R_{i}$
, induces an equivalence with the full subcategory of globally bounded families of perfect complexes.
$p_{i}:R\rightarrow R_{i}$
, induces an equivalence with the full subcategory of globally bounded families of perfect complexes.
In particular, this theorem implies that we have a fully faithful functor
 $$\begin{eqnarray}\mathsf{Perf}(R){\hookrightarrow}\mathop{\prod }_{i\in I}\mathsf{Perf}(R_{i}),\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Perf}(R){\hookrightarrow}\mathop{\prod }_{i\in I}\mathsf{Perf}(R_{i}),\end{eqnarray}$$
and, moreover, it characterises the essential image of this embedding. The functor
 $\mathsf{QC}(R)\rightarrow \prod _{i\in I}\mathsf{QC}(R_{i})$
is not fully faithful. In the following example we illustrate this behaviour by alluding to classical, non-derived tensor products and modules over infinite product rings.
$\mathsf{QC}(R)\rightarrow \prod _{i\in I}\mathsf{QC}(R_{i})$
is not fully faithful. In the following example we illustrate this behaviour by alluding to classical, non-derived tensor products and modules over infinite product rings.
Example 3.17. Let
![]() $I$
be an infinite small set and
$I$
be an infinite small set and
![]() $\{R_{i}\}_{i\in I}$
a collection of non-trivial rings. Let
$\{R_{i}\}_{i\in I}$
a collection of non-trivial rings. Let
 $R=\prod _{i\in I}R_{i}$
be the infinite product. We define an equivalence relation
$R=\prod _{i\in I}R_{i}$
be the infinite product. We define an equivalence relation
![]() ${\sim}$
on
${\sim}$
on
![]() $R$
, where we say that
$R$
, where we say that
 $(x_{i})_{i\in I}\sim (y_{i})_{i\in I}$
, if and only if
$(x_{i})_{i\in I}\sim (y_{i})_{i\in I}$
, if and only if
![]() $x_{i}=y_{i}$
for all but finitely many indices
$x_{i}=y_{i}$
for all but finitely many indices
![]() $i$
. We define the
$i$
. We define the
![]() $R$
-module
$R$
-module
![]() $M$
to be
$M$
to be
![]() $R/\sim$
. By construction, we have
$R/\sim$
. By construction, we have
 $M\otimes _{R}R_{i}=0$
for all
$M\otimes _{R}R_{i}=0$
for all
![]() $i\in I$
, although
$i\in I$
, although
![]() $M\neq 0$
.
$M\neq 0$
.
This failure of fidelity is the reason that we cannot expect the functor
 $\mathsf{QC}(X)\rightarrow |\mathsf{QC}(\mathbb{A}_{X}^{\bullet })|$
to be an equivalence. This remark will become clear by inspecting the argument of Lemma 3.21 below.
$\mathsf{QC}(X)\rightarrow |\mathsf{QC}(\mathbb{A}_{X}^{\bullet })|$
to be an equivalence. This remark will become clear by inspecting the argument of Lemma 3.21 below.
3.1.4 Conservativity
The following assertion is key in our argument that
![]() $-\otimes \mathsf{A}_{X}^{\bullet }$
is an equivalence of categories, with inverse
$-\otimes \mathsf{A}_{X}^{\bullet }$
is an equivalence of categories, with inverse
![]() $\int$
.
$\int$
.
Proposition 3.18. If
![]() $X$
is affine, then the functor
$X$
is affine, then the functor
 $\int :|\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|\rightarrow \mathsf{QC}(X)$
is conservative.
$\int :|\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|\rightarrow \mathsf{QC}(X)$
is conservative.
The proof is scattered over this subsection, and broken down into several lemmas. Our argument relies on two technical results: an invariance property for derived
![]() $\infty$
-categories with set-theoretic support condition, given by the Thomason–Trobaugh theorem [Reference Thomason and TrobaughTT90, Theorem 2.6.3], and the theory of modules over product rings, described in § 3.1.3. For the convenience of the reader, we have allowed ourselves to state Thomason–Trobaugh’s result in a way which can be directly applied to our context. We refer the reader to the original reference for a more general statement.
$\infty$
-categories with set-theoretic support condition, given by the Thomason–Trobaugh theorem [Reference Thomason and TrobaughTT90, Theorem 2.6.3], and the theory of modules over product rings, described in § 3.1.3. For the convenience of the reader, we have allowed ourselves to state Thomason–Trobaugh’s result in a way which can be directly applied to our context. We refer the reader to the original reference for a more general statement.
Theorem 3.19 (Thomason–Trobaugh).
Let
![]() $R$
be a Noetherian ring, let
$R$
be a Noetherian ring, let
![]() $I$
be an ideal and let
$I$
be an ideal and let
 $\mathsf{Perf}_{I}(R)$
denote the full subcategory of
$\mathsf{Perf}_{I}(R)$
denote the full subcategory of
![]() $\mathsf{Perf}(R)$
consisting of perfect complexes set-theoretically supported at the closed subset of
$\mathsf{Perf}(R)$
consisting of perfect complexes set-theoretically supported at the closed subset of
![]() $\operatorname{Spec}R$
corresponding to
$\operatorname{Spec}R$
corresponding to
![]() $I$
. We denote by
$I$
. We denote by
![]() $\widehat{R}_{I}$
the completion of
$\widehat{R}_{I}$
the completion of
![]() $R$
at
$R$
at
![]() $I$
. Then, tensoring along
$I$
. Then, tensoring along
 $R\rightarrow \widehat{R}_{I}$
induces an equivalence of symmetric monoidal
$R\rightarrow \widehat{R}_{I}$
induces an equivalence of symmetric monoidal
![]() $\infty$
-categories
$\infty$
-categories
 $\mathsf{Perf}_{I}(R)\cong \mathsf{Perf}_{\widehat{I}}(\widehat{R}_{I})$
.
$\mathsf{Perf}_{I}(R)\cong \mathsf{Perf}_{\widehat{I}}(\widehat{R}_{I})$
.
From now on we fix
 $0\neq N^{\bullet }\in \mathsf{Perf}(\mathsf{A}_{X}^{\bullet })$
; and will show that
$0\neq N^{\bullet }\in \mathsf{Perf}(\mathsf{A}_{X}^{\bullet })$
; and will show that
 $\int N^{\bullet }\neq 0$
. We begin with an easy observation first.
$\int N^{\bullet }\neq 0$
. We begin with an easy observation first.
Lemma 3.20. Let
![]() $X$
be an affine Noetherian scheme. For every
$X$
be an affine Noetherian scheme. For every
 $0\neq N^{\bullet }\in \mathsf{Perf}(\mathsf{A}_{X}^{\bullet })$
there exists a point
$0\neq N^{\bullet }\in \mathsf{Perf}(\mathsf{A}_{X}^{\bullet })$
there exists a point
![]() $x\in X$
, and a perfect complex
$x\in X$
, and a perfect complex
 $F\in \mathsf{Perf}_{\{x\}}(X)$
, such that
$F\in \mathsf{Perf}_{\{x\}}(X)$
, such that
 $F\otimes _{{\mathcal{O}}_{X}}N^{\bullet }\neq 0$
.
$F\otimes _{{\mathcal{O}}_{X}}N^{\bullet }\neq 0$
.
Proof. Since
![]() $N^{0}\neq 0$
, it follows from Bhatt’s Theorem 3.16 that there is a (not necessarily closed) point
$N^{0}\neq 0$
, it follows from Bhatt’s Theorem 3.16 that there is a (not necessarily closed) point
![]() $x\in X$
with
$x\in X$
with
 $N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{x}\neq 0$
. Since
$N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{x}\neq 0$
. Since
![]() $N^{\bullet }$
is non-zero there exists a point
$N^{\bullet }$
is non-zero there exists a point
![]() $x\in X$
, such that the perfect complex of
$x\in X$
, such that the perfect complex of
![]() $\widehat{{\mathcal{O}}_{x}}$
-modules
$\widehat{{\mathcal{O}}_{x}}$
-modules
 $N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{x}$
is non-zero. The Yoneda embedding restricts to a fully faithful functor
$N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{x}$
is non-zero. The Yoneda embedding restricts to a fully faithful functor
 $\mathsf{Perf}(\widehat{{\mathcal{O}}}_{x}){\hookrightarrow}\mathsf{Ind}\mathsf{Perf}_{\{x\}}(X)$
(see the reformulation of [Reference EfimovEfi10] in [Reference Braunling, Groechenig and WolfsonBGW14, Propositions 5.2 and 5.4]). Therefore, there exists an object
$\mathsf{Perf}(\widehat{{\mathcal{O}}}_{x}){\hookrightarrow}\mathsf{Ind}\mathsf{Perf}_{\{x\}}(X)$
(see the reformulation of [Reference EfimovEfi10] in [Reference Braunling, Groechenig and WolfsonBGW14, Propositions 5.2 and 5.4]). Therefore, there exists an object
 $F\in \mathsf{Perf}_{\{x\}}(X)$
, such that
$F\in \mathsf{Perf}_{\{x\}}(X)$
, such that
 $\text{}\underline{\mathsf{Hom}}(F^{\vee },N^{\bullet }\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{x})=F\otimes _{{\mathcal{O}}_{X}}N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{x}\neq 0$
. This implies
$\text{}\underline{\mathsf{Hom}}(F^{\vee },N^{\bullet }\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{x})=F\otimes _{{\mathcal{O}}_{X}}N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{x}\neq 0$
. This implies
 $F\otimes _{{\mathcal{O}}_{X}}N^{\bullet }\neq 0$
.◻
$F\otimes _{{\mathcal{O}}_{X}}N^{\bullet }\neq 0$
.◻
Lemma 3.21. If
![]() $X$
is affine, and
$X$
is affine, and
 $N^{\bullet }\in \mathsf{Perf}(\mathsf{A}_{X}^{\bullet })$
, then there exists a closed point
$N^{\bullet }\in \mathsf{Perf}(\mathsf{A}_{X}^{\bullet })$
, then there exists a closed point
![]() $x\in X$
such that
$x\in X$
such that
 $N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{x}\neq 0$
.
$N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{x}\neq 0$
.
Proof. We apply Lemma 3.20 to deduce the existence of a (not necessarily closed) point
![]() $y\in X$
, such that
$y\in X$
, such that
 $N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{y}\neq 0$
. We choose
$N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{y}\neq 0$
. We choose
 $F\in \mathsf{Perf}_{\{y\}}(\widehat{{\mathcal{O}}}_{y})$
, such that
$F\in \mathsf{Perf}_{\{y\}}(\widehat{{\mathcal{O}}}_{y})$
, such that
 $N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}_{y}}\otimes _{\widehat{{\mathcal{O}}}_{y}}F\neq 0$
(existence of such a point
$N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}_{y}}\otimes _{\widehat{{\mathcal{O}}}_{y}}F\neq 0$
(existence of such a point
![]() $y$
and a complex
$y$
and a complex
![]() $F$
are guaranteed by Lemma 3.20). It is clear that
$F$
are guaranteed by Lemma 3.20). It is clear that
 $N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{y}\otimes _{{\mathcal{O}}_{y}}F\neq 0$
implies
$N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{y}\otimes _{{\mathcal{O}}_{y}}F\neq 0$
implies
 $N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}_{y}}\neq 0$
. This justifies making this replacement. However, note that
$N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}_{y}}\neq 0$
. This justifies making this replacement. However, note that
 $N^{\bullet }\otimes _{{\mathcal{O}}_{X}}F\in \mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
, because
$N^{\bullet }\otimes _{{\mathcal{O}}_{X}}F\in \mathsf{QC}(\mathsf{A}_{X}^{\bullet })$
, because
![]() $F$
might not be perfect as a complex of
$F$
might not be perfect as a complex of
![]() ${\mathcal{O}}_{X}$
-module. Nonetheless we may view
${\mathcal{O}}_{X}$
-module. Nonetheless we may view
 $N^{0}\otimes _{{\mathcal{O}}_{X}}F$
as an object in
$N^{0}\otimes _{{\mathcal{O}}_{X}}F$
as an object in
 $\mathsf{Perf}_{\{y\}}({\mathcal{O}}_{y})$
.
$\mathsf{Perf}_{\{y\}}({\mathcal{O}}_{y})$
.
Let
 $x\in \overline{\{y\}}$
be a closed point. Observe that such an
$x\in \overline{\{y\}}$
be a closed point. Observe that such an
![]() $x$
exists, because
$x$
exists, because
![]() $X$
is affine (every ideal is contained in a maximal ideal). We claim that
$X$
is affine (every ideal is contained in a maximal ideal). We claim that
 $N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}_{x}}\neq 0$
as well. Indeed, we have a map co-simplicial sheaves of algebras
$N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}_{x}}\neq 0$
as well. Indeed, we have a map co-simplicial sheaves of algebras
 $f:\mathsf{A}_{X}^{\bullet }\rightarrow \mathsf{A}_{X,T_{\bullet }}^{\bullet }$
, where
$f:\mathsf{A}_{X}^{\bullet }\rightarrow \mathsf{A}_{X,T_{\bullet }}^{\bullet }$
, where
 $T_{\bullet }\subset |X|_{\bullet }$
is the minimal simplicial subset containing the chains
$T_{\bullet }\subset |X|_{\bullet }$
is the minimal simplicial subset containing the chains
![]() $(x)$
,
$(x)$
,
![]() $(y)$
, and
$(y)$
, and
![]() $(x<y)$
.
$(x<y)$
.
By [Reference HuberHub91, Proposition 3.3.3], the ring
![]() $\mathsf{A}_{X,T_{1}}^{1}$
is isomorphic to a product
$\mathsf{A}_{X,T_{1}}^{1}$
is isomorphic to a product
 $\mathsf{A}^{0}\times \mathsf{A}(x<z)$
, where the first factor corresponds to the degenerate part of the co-simplicial ring.
$\mathsf{A}^{0}\times \mathsf{A}(x<z)$
, where the first factor corresponds to the degenerate part of the co-simplicial ring.
The maps
 $\mathsf{A}_{X}^{0}\rightarrow \widehat{{\mathcal{O}}}_{z}$
for
$\mathsf{A}_{X}^{0}\rightarrow \widehat{{\mathcal{O}}}_{z}$
for
 $z=x,y$
factor through
$z=x,y$
factor through
 $\mathsf{A}_{X,T_{0}}^{0}({\mathcal{O}}_{X})$
. We have the following commutative diagram (see [Reference HuberHub91, Proposition 3.2.1] for how
$\mathsf{A}_{X,T_{0}}^{0}({\mathcal{O}}_{X})$
. We have the following commutative diagram (see [Reference HuberHub91, Proposition 3.2.1] for how
 $\mathsf{A}(x<y)$
fits in there).
$\mathsf{A}(x<y)$
fits in there).

We recall that the set-theoretic support condition
 $N^{\bullet }\otimes _{{\mathcal{O}}_{X}}F\in \mathsf{QC}_{\{y\}}({\mathcal{O}}_{y})\cong \mathsf{QC}_{\{y\}}(\widehat{{\mathcal{O}}}_{y})$
holds (where the equivalence is given by pullback, see Thomason–Trobaugh’s theorem (Theorem 3.19)), and we assume by contradiction
$N^{\bullet }\otimes _{{\mathcal{O}}_{X}}F\in \mathsf{QC}_{\{y\}}({\mathcal{O}}_{y})\cong \mathsf{QC}_{\{y\}}(\widehat{{\mathcal{O}}}_{y})$
holds (where the equivalence is given by pullback, see Thomason–Trobaugh’s theorem (Theorem 3.19)), and we assume by contradiction
 $N^{0}\otimes _{\mathsf{A}^{0}}\widehat{{\mathcal{O}}}_{x}=0$
. The first line of the commutative diagram contains the two face maps of the co-simplicial object
$N^{0}\otimes _{\mathsf{A}^{0}}\widehat{{\mathcal{O}}}_{x}=0$
. The first line of the commutative diagram contains the two face maps of the co-simplicial object
![]() $\mathsf{A}_{X,T_{\bullet }}^{\bullet }$
. Using our assumptions we therefore obtain
$\mathsf{A}_{X,T_{\bullet }}^{\bullet }$
. Using our assumptions we therefore obtain
 $$\begin{eqnarray}(N^{0}\otimes _{{\mathcal{O}}_{X}}F\otimes _{\mathsf{A}^{0}}\widehat{{\mathcal{O}}}_{y})\times _{\widehat{{\mathcal{O}}}_{y}}\mathsf{A}(x<y)\simeq N^{0}\otimes _{{\mathcal{O}}_{X}}F\otimes _{\mathsf{A}^{0}}\widehat{{\mathcal{O}}}_{x}=0.\end{eqnarray}$$
$$\begin{eqnarray}(N^{0}\otimes _{{\mathcal{O}}_{X}}F\otimes _{\mathsf{A}^{0}}\widehat{{\mathcal{O}}}_{y})\times _{\widehat{{\mathcal{O}}}_{y}}\mathsf{A}(x<y)\simeq N^{0}\otimes _{{\mathcal{O}}_{X}}F\otimes _{\mathsf{A}^{0}}\widehat{{\mathcal{O}}}_{x}=0.\end{eqnarray}$$
Since
 $N^{0}\otimes _{{\mathcal{O}}_{X}}F\in \mathsf{Perf}_{\{y\}}({\mathcal{O}}_{Y})\simeq \mathsf{Perf}_{\{y\}}(\widehat{{\mathcal{O}}}_{Y})$
(using Thomason–Trobaugh’s theorem (Theorem 3.19)), commutativity of the left-hand square implies therefore
$N^{0}\otimes _{{\mathcal{O}}_{X}}F\in \mathsf{Perf}_{\{y\}}({\mathcal{O}}_{Y})\simeq \mathsf{Perf}_{\{y\}}(\widehat{{\mathcal{O}}}_{Y})$
(using Thomason–Trobaugh’s theorem (Theorem 3.19)), commutativity of the left-hand square implies therefore
 $$\begin{eqnarray}(N^{0}\otimes _{{\mathcal{O}}_{X}}F\otimes _{\mathsf{A}^{0}}\widehat{{\mathcal{O}}}_{y})\otimes _{{\mathcal{O}}_{y}}(\widehat{{\mathcal{O}}}_{x}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{y})=0.\end{eqnarray}$$
$$\begin{eqnarray}(N^{0}\otimes _{{\mathcal{O}}_{X}}F\otimes _{\mathsf{A}^{0}}\widehat{{\mathcal{O}}}_{y})\otimes _{{\mathcal{O}}_{y}}(\widehat{{\mathcal{O}}}_{x}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{y})=0.\end{eqnarray}$$
The ring homomorphism
 ${\mathcal{O}}_{y}\rightarrow \widehat{{\mathcal{O}}}_{x}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{y}$
is the co-base change of the fully faithful ring homomorphism
${\mathcal{O}}_{y}\rightarrow \widehat{{\mathcal{O}}}_{x}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{y}$
is the co-base change of the fully faithful ring homomorphism
 ${\mathcal{O}}_{x}\rightarrow \widehat{{\mathcal{O}}}_{x}$
. Therefore, we have
${\mathcal{O}}_{x}\rightarrow \widehat{{\mathcal{O}}}_{x}$
. Therefore, we have
 $N^{0}\otimes _{{\mathcal{O}}_{X}}F\otimes _{\mathsf{A}^{0}}\widehat{{\mathcal{O}}}_{y}=0$
, which is a contradiction.◻
$N^{0}\otimes _{{\mathcal{O}}_{X}}F\otimes _{\mathsf{A}^{0}}\widehat{{\mathcal{O}}}_{y}=0$
, which is a contradiction.◻
The following lemma could also be deduced from a more elementary argument. We give a more abstract proof, which uses a categorical viewpoint on ring completions.
Lemma 3.22. Let
![]() $X$
be an affine Noetherian scheme. For every
$X$
be an affine Noetherian scheme. For every
 $0\neq N^{\bullet }\in \mathsf{Perf}(\mathsf{A}_{X}^{\bullet })$
there exists a closed point
$0\neq N^{\bullet }\in \mathsf{Perf}(\mathsf{A}_{X}^{\bullet })$
there exists a closed point
![]() $x\in X$
, and a perfect complex
$x\in X$
, and a perfect complex
 $F\in \mathsf{Perf}_{\{x\}}(X)$
, such that
$F\in \mathsf{Perf}_{\{x\}}(X)$
, such that
 $F\otimes _{{\mathcal{O}}_{X}}N^{\bullet }\neq 0$
.
$F\otimes _{{\mathcal{O}}_{X}}N^{\bullet }\neq 0$
.
Proof. We have seen in Lemma 3.21 that there exists a closed point
![]() $x\in X$
, such that the perfect complex of
$x\in X$
, such that the perfect complex of
![]() $\widehat{{\mathcal{O}}_{x}}$
-modules
$\widehat{{\mathcal{O}}_{x}}$
-modules
 $N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{x}$
is non-zero. Using the strategy as in the proof of Lemma 3.20, we deduce the existence of a perfect complex
$N^{0}\otimes _{\mathsf{A}_{X}^{0}}\widehat{{\mathcal{O}}}_{x}$
is non-zero. Using the strategy as in the proof of Lemma 3.20, we deduce the existence of a perfect complex
 $F\in \mathsf{Perf}_{\{x\}}(X)$
, such that
$F\in \mathsf{Perf}_{\{x\}}(X)$
, such that
 $F\otimes _{{\mathcal{O}}_{X}}N^{\bullet }\neq 0$
.◻
$F\otimes _{{\mathcal{O}}_{X}}N^{\bullet }\neq 0$
.◻
In the following we denote by
![]() ${\mathcal{H}}^{i}(-)$
the degree
${\mathcal{H}}^{i}(-)$
the degree
![]() $i$
cohomology sheaf of a complex of sheaves. Recall that we have functors
$i$
cohomology sheaf of a complex of sheaves. Recall that we have functors
 $\mathsf{A}_{X,T}(-):\mathsf{QCoh}(X)\rightarrow \mathsf{Mod}({\mathcal{O}}_{X})$
, as defined in Definition 1.4. As before, we denote by
$\mathsf{A}_{X,T}(-):\mathsf{QCoh}(X)\rightarrow \mathsf{Mod}({\mathcal{O}}_{X})$
, as defined in Definition 1.4. As before, we denote by
![]() $\mathsf{A}_{X}^{0}(-)$
the functor for
$\mathsf{A}_{X}^{0}(-)$
the functor for
 $T=|X|$
.
$T=|X|$
.
Lemma 3.23. Let
 $M\in \mathsf{QC}(X)=\mathsf{Ind}\mathsf{Perf}(X)$
, then
$M\in \mathsf{QC}(X)=\mathsf{Ind}\mathsf{Perf}(X)$
, then
 ${\mathcal{H}}^{i}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X,T})\simeq \mathsf{A}_{X,T}({\mathcal{H}}^{i}(M))$
.
${\mathcal{H}}^{i}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X,T})\simeq \mathsf{A}_{X,T}({\mathcal{H}}^{i}(M))$
.
Proof. By definition, the functor
 $\mathsf{A}_{X,T}(-)\simeq \mathsf{QCoh}(X)\rightarrow \mathsf{Mod}({\mathcal{O}}_{X})$
commutes with filtered colimits. Since the same is true for
$\mathsf{A}_{X,T}(-)\simeq \mathsf{QCoh}(X)\rightarrow \mathsf{Mod}({\mathcal{O}}_{X})$
commutes with filtered colimits. Since the same is true for
![]() ${\mathcal{H}}^{i}(-)$
and
${\mathcal{H}}^{i}(-)$
and
 $-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X,T}({\mathcal{O}}_{X})$
, we see that we may assume that
$-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X,T}({\mathcal{O}}_{X})$
, we see that we may assume that
![]() $M$
is a perfect complex. Since the statement is local, we may assume that
$M$
is a perfect complex. Since the statement is local, we may assume that
![]() $M$
can be represented by a bounded complex
$M$
can be represented by a bounded complex
![]() $(V^{\bullet })$
of free sheaves of finite generation
$(V^{\bullet })$
of free sheaves of finite generation
 $V^{i}={\mathcal{O}}_{X}^{m_{i}}$
. In particular,
$V^{i}={\mathcal{O}}_{X}^{m_{i}}$
. In particular,
![]() ${\mathcal{H}}^{i}$
is represented as the cohomology sheaf in degree
${\mathcal{H}}^{i}$
is represented as the cohomology sheaf in degree
![]() $i$
of the chain complex
$i$
of the chain complex
 $$\begin{eqnarray}\cdots \rightarrow {\mathcal{O}}_{X}^{m_{i-1}}\rightarrow {\mathcal{O}}_{X}^{m_{i}}\rightarrow {\mathcal{O}}_{X}^{m_{i+1}}\rightarrow \cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}\cdots \rightarrow {\mathcal{O}}_{X}^{m_{i-1}}\rightarrow {\mathcal{O}}_{X}^{m_{i}}\rightarrow {\mathcal{O}}_{X}^{m_{i+1}}\rightarrow \cdots \,.\end{eqnarray}$$
Since
 $\mathsf{A}_{X,T}(-)$
is exact, we obtain a chain complex
$\mathsf{A}_{X,T}(-)$
is exact, we obtain a chain complex
 $$\begin{eqnarray}\cdots \rightarrow \mathsf{A}_{X,T}({\mathcal{O}}_{X}^{m_{i-1}})\rightarrow \mathsf{A}_{X,T}({\mathcal{O}}_{X}^{m_{i}})\rightarrow \mathsf{A}_{X,T}({\mathcal{O}}_{X}^{m_{i-1}})\rightarrow \cdots \,,\end{eqnarray}$$
$$\begin{eqnarray}\cdots \rightarrow \mathsf{A}_{X,T}({\mathcal{O}}_{X}^{m_{i-1}})\rightarrow \mathsf{A}_{X,T}({\mathcal{O}}_{X}^{m_{i}})\rightarrow \mathsf{A}_{X,T}({\mathcal{O}}_{X}^{m_{i-1}})\rightarrow \cdots \,,\end{eqnarray}$$
and an equivalence of middle cohomology sheaves. The second chain complex can be identified with
 $M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X,T}$
. This implies the assertion.◻
$M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X,T}$
. This implies the assertion.◻
Proof of Proposition 3.18.
Let
 $0\neq N^{\bullet }\in \mathsf{Perf}(\mathsf{A}_{X}^{\bullet })$
and
$0\neq N^{\bullet }\in \mathsf{Perf}(\mathsf{A}_{X}^{\bullet })$
and
 $F\in \mathsf{Perf}(X)$
as in Lemma 3.22. In particular, there exists a closed point
$F\in \mathsf{Perf}(X)$
as in Lemma 3.22. In particular, there exists a closed point
![]() $x$
, such that
$x$
, such that
 $F\in \mathsf{Perf}_{\{x\}}(X)$
. By the projection formula (Lemma 3.11) we have
$F\in \mathsf{Perf}_{\{x\}}(X)$
. By the projection formula (Lemma 3.11) we have
 $$\begin{eqnarray}\int (N^{\bullet }\otimes _{{\mathcal{O}}_{X}}F)\cong F\otimes _{{\mathcal{O}}_{X}}\int N^{\bullet }.\end{eqnarray}$$
$$\begin{eqnarray}\int (N^{\bullet }\otimes _{{\mathcal{O}}_{X}}F)\cong F\otimes _{{\mathcal{O}}_{X}}\int N^{\bullet }.\end{eqnarray}$$
Therefore, it suffices to show that this expression is
![]() $\neq 0$
, to deduce that
$\neq 0$
, to deduce that
 $\int N^{\bullet }\neq 0$
. Henceforth, we replace
$\int N^{\bullet }\neq 0$
. Henceforth, we replace
![]() $N^{\bullet }$
by
$N^{\bullet }$
by
 $N^{\bullet }\otimes F$
, that is, we have
$N^{\bullet }\otimes F$
, that is, we have
 $N^{\bullet }|_{X\setminus \{x\}}=0$
. Since pullback along
$N^{\bullet }|_{X\setminus \{x\}}=0$
. Since pullback along
 $\operatorname{Spec}\widehat{{\mathcal{O}}}_{x}\rightarrow X$
induces an equivalence of
$\operatorname{Spec}\widehat{{\mathcal{O}}}_{x}\rightarrow X$
induces an equivalence of
![]() $\infty$
-categories (using Thomason–Trobaugh’s theorem (Theorem 3.19))
$\infty$
-categories (using Thomason–Trobaugh’s theorem (Theorem 3.19))
 $$\begin{eqnarray}\mathsf{Perf}_{\{x\}}(X)\rightarrow \mathsf{Perf}_{\{x\}}(\widehat{{\mathcal{O}}}_{x}),\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Perf}_{\{x\}}(X)\rightarrow \mathsf{Perf}_{\{x\}}(\widehat{{\mathcal{O}}}_{x}),\end{eqnarray}$$
one obtains
 $N^{0}\cong M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0}$
, for some
$N^{0}\cong M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0}$
, for some
 $M\in \mathsf{Perf}_{\{x\}}(X)$
. Let
$M\in \mathsf{Perf}_{\{x\}}(X)$
. Let
 $d_{i}:\mathsf{A}_{X}^{0}\rightarrow \mathsf{A}_{X}^{n}$
be an arbitrary boundary map, and
$d_{i}:\mathsf{A}_{X}^{0}\rightarrow \mathsf{A}_{X}^{n}$
be an arbitrary boundary map, and
 $\unicode[STIX]{x1D719}_{i}:{\mathcal{O}}_{X}\rightarrow \mathsf{A}_{X}^{n}$
the map given by composition with the augmentation. We claim that
$\unicode[STIX]{x1D719}_{i}:{\mathcal{O}}_{X}\rightarrow \mathsf{A}_{X}^{n}$
the map given by composition with the augmentation. We claim that
 $M\rightarrow M\otimes \mathsf{A}_{X}^{n}$
is a quasi-isomorphism of complexes of
$M\rightarrow M\otimes \mathsf{A}_{X}^{n}$
is a quasi-isomorphism of complexes of
![]() ${\mathcal{O}}_{X}$
-modules. Indeed, passing to the cohomology sheaves, we obtain using Lemma 3.23
${\mathcal{O}}_{X}$
-modules. Indeed, passing to the cohomology sheaves, we obtain using Lemma 3.23
 $$\begin{eqnarray}{\mathcal{H}}^{i}(M)\rightarrow \mathsf{A}_{X}^{n}({\mathcal{H}}^{i}(M)).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{i}(M)\rightarrow \mathsf{A}_{X}^{n}({\mathcal{H}}^{i}(M)).\end{eqnarray}$$
This is an isomorphism, since
![]() ${\mathcal{H}}^{i}(M)$
is set-theoretically supported at the closed point
${\mathcal{H}}^{i}(M)$
is set-theoretically supported at the closed point
![]() $x$
(Remark 1.9).
$x$
(Remark 1.9).
Hence, we see that
 $N^{\bullet }\otimes _{{\mathcal{O}}_{X}}F$
is equivalent to the constant object
$N^{\bullet }\otimes _{{\mathcal{O}}_{X}}F$
is equivalent to the constant object
 $M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }$
in
$M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }$
in
 $\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })$
, which implies
$\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })$
, which implies
 $\int N^{\bullet }\otimes _{{\mathcal{O}}_{X}}F\cong N^{0}\otimes _{{\mathcal{O}}_{X}}F\neq 0$
. ◻
$\int N^{\bullet }\otimes _{{\mathcal{O}}_{X}}F\cong N^{0}\otimes _{{\mathcal{O}}_{X}}F\neq 0$
. ◻
3.1.5 Conclusion of the argument
Henceforth, we assume that
![]() $X$
is an affine Noetherian scheme. In this subsection we prove that for
$X$
is an affine Noetherian scheme. In this subsection we prove that for
 $M^{\bullet }\in |\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|$
the object
$M^{\bullet }\in |\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|$
the object
![]() $\int M^{\bullet }$
is also perfect. We first show (Corollary 3.28) that this statement holds generically, that is, there exists a non-empty open subset
$\int M^{\bullet }$
is also perfect. We first show (Corollary 3.28) that this statement holds generically, that is, there exists a non-empty open subset
![]() $U\subset X$
, such that
$U\subset X$
, such that
 $\int M^{\bullet }|_{U}\in \mathsf{Perf}(U)$
. We use this result as a stepping stone, together with the Noetherian property of
$\int M^{\bullet }|_{U}\in \mathsf{Perf}(U)$
. We use this result as a stepping stone, together with the Noetherian property of
![]() $X$
, to show that
$X$
, to show that
![]() $\int M^{\bullet }$
is in fact a perfect complex. The key observation to deduce this, is Lemma 3.26, which asserts that for a generic point
$\int M^{\bullet }$
is in fact a perfect complex. The key observation to deduce this, is Lemma 3.26, which asserts that for a generic point
![]() $\unicode[STIX]{x1D702}$
of
$\unicode[STIX]{x1D702}$
of
![]() $X$
,
$X$
,
 $M^{0}\otimes _{\mathsf{A}_{X}^{0}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}\simeq 0$
implies the existence of a non-empty open subset
$M^{0}\otimes _{\mathsf{A}_{X}^{0}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}\simeq 0$
implies the existence of a non-empty open subset
![]() $V\subset X$
, such that
$V\subset X$
, such that
 $M^{\bullet }|_{V}\simeq 0$
.
$M^{\bullet }|_{V}\simeq 0$
.
Lemma 3.24. Let
![]() $X$
be a Noetherian scheme and let
$X$
be a Noetherian scheme and let
 $|Z|\subset X$
be a closed subset, with
$|Z|\subset X$
be a closed subset, with
![]() $\unicode[STIX]{x1D702}$
a generic point of
$\unicode[STIX]{x1D702}$
a generic point of
![]() $|Z|$
and
$|Z|$
and
![]() $U$
an affine open neighbourhood of
$U$
an affine open neighbourhood of
![]() $\unicode[STIX]{x1D702}$
such that
$\unicode[STIX]{x1D702}$
such that
![]() $U\cap |Z|$
is irreducible. We have that the canonical map
$U\cap |Z|$
is irreducible. We have that the canonical map
 $\mathsf{A}_{X,|Z|_{\bullet }}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})|_{U}\rightarrow \widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}}$
is a homotopy equivalence of co-simplicial sheaves of algebras.
$\mathsf{A}_{X,|Z|_{\bullet }}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})|_{U}\rightarrow \widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}}$
is a homotopy equivalence of co-simplicial sheaves of algebras.
We refer the reader to [Sta, Tag 019U] for a detailed review of the definition of a homotopy between maps of co-simplicial objects in a category
![]() $\mathsf{C}$
. In brief, we say that
$\mathsf{C}$
. In brief, we say that
![]() $f$
,
$f$
,
 $g:U^{\bullet }\rightarrow V^{\bullet }$
are homotopic, if for every
$g:U^{\bullet }\rightarrow V^{\bullet }$
are homotopic, if for every
![]() $n\geqslant 0$
and every
$n\geqslant 0$
and every
 $\unicode[STIX]{x1D6FC}:[n]\rightarrow [1]$
we have maps
$\unicode[STIX]{x1D6FC}:[n]\rightarrow [1]$
we have maps
 $h^{n,\unicode[STIX]{x1D6FC}}:U^{n}\rightarrow V^{n}$
, such that for
$h^{n,\unicode[STIX]{x1D6FC}}:U^{n}\rightarrow V^{n}$
, such that for
 $f:[k]\rightarrow [n]$
the diagram
$f:[k]\rightarrow [n]$
the diagram

commutes. We also require that the original maps
![]() $f^{n}$
and
$f^{n}$
and
![]() $g^{n}$
are obtained as
$g^{n}$
are obtained as
![]() $h^{n,0}$
and
$h^{n,0}$
and
![]() $h^{n,1}$
, where
$h^{n,1}$
, where
 $i:[n]\rightarrow [1]$
is the constant map with value
$i:[n]\rightarrow [1]$
is the constant map with value
![]() $i$
, for
$i$
, for
![]() $i\in [1]$
.
$i\in [1]$
.
There is an equivalent definition, which makes sense in any
![]() $\infty$
-category, possessing finite products, so in particular in the
$\infty$
-category, possessing finite products, so in particular in the
![]() $\infty$
-category of small
$\infty$
-category of small
![]() $\infty$
-categories. We refer the reader to Definition A.8. In Lemma A.9 we show that two homotopy equivalent co-simplicial objects in
$\infty$
-categories. We refer the reader to Definition A.8. In Lemma A.9 we show that two homotopy equivalent co-simplicial objects in
![]() $\infty$
-categories have canonically equivalent limit
$\infty$
-categories have canonically equivalent limit
![]() $\infty$
-categories.
$\infty$
-categories.
There is also a notion of homotopy for maps between simplicial sets. Let
![]() $S_{{\leqslant}}$
be a partially ordered set, with a maximal element
$S_{{\leqslant}}$
be a partially ordered set, with a maximal element
![]() $\unicode[STIX]{x1D702}$
, and we will mainly care about
$\unicode[STIX]{x1D702}$
, and we will mainly care about
 $S_{{\leqslant}}=|U\cap Z|_{{\leqslant}}$
with the generic point
$S_{{\leqslant}}=|U\cap Z|_{{\leqslant}}$
with the generic point
![]() $\unicode[STIX]{x1D702}$
. We have the simplicial set of ordered chains
$\unicode[STIX]{x1D702}$
. We have the simplicial set of ordered chains
![]() $S_{\bullet }$
, where
$S_{\bullet }$
, where
 $S_{n}=\{x_{0}\leqslant \cdots \leqslant x_{n}\}$
. We have a homotopy
$S_{n}=\{x_{0}\leqslant \cdots \leqslant x_{n}\}$
. We have a homotopy
 $$\begin{eqnarray}h_{n,\unicode[STIX]{x1D6FC}}(x_{0}\leqslant \cdots \leqslant x_{n})=x_{0}\leqslant \cdots \leqslant x_{k}\leqslant \unicode[STIX]{x1D702}\cdots \leqslant \unicode[STIX]{x1D702},\end{eqnarray}$$
$$\begin{eqnarray}h_{n,\unicode[STIX]{x1D6FC}}(x_{0}\leqslant \cdots \leqslant x_{n})=x_{0}\leqslant \cdots \leqslant x_{k}\leqslant \unicode[STIX]{x1D702}\cdots \leqslant \unicode[STIX]{x1D702},\end{eqnarray}$$
where
![]() $k$
is the maximal element of
$k$
is the maximal element of
![]() $[n]$
, such that
$[n]$
, such that
 $\unicode[STIX]{x1D6FC}(k)=0$
. This defines a homotopy between the identity of the simplicial set
$\unicode[STIX]{x1D6FC}(k)=0$
. This defines a homotopy between the identity of the simplicial set
![]() $S_{\bullet }$
of ordered chains and the constant map
$S_{\bullet }$
of ordered chains and the constant map
 $S_{\bullet }\rightarrow \{\unicode[STIX]{x1D702}\}\subset S_{\bullet }$
. In other words, the constant simplicial set
$S_{\bullet }\rightarrow \{\unicode[STIX]{x1D702}\}\subset S_{\bullet }$
. In other words, the constant simplicial set
![]() $\{\unicode[STIX]{x1D702}\}_{\bullet }$
is a deformation retract of
$\{\unicode[STIX]{x1D702}\}_{\bullet }$
is a deformation retract of
![]() $S_{\bullet }$
. This is a minor variation of [Sta, Tag 08Q3]. The proof of the lemma above will use this homotopy
$S_{\bullet }$
. This is a minor variation of [Sta, Tag 08Q3]. The proof of the lemma above will use this homotopy
![]() $h_{n,\unicode[STIX]{x1D6FC}}$
, which contracts
$h_{n,\unicode[STIX]{x1D6FC}}$
, which contracts
 $|U\cap Z|_{\bullet }$
onto the generic point.
$|U\cap Z|_{\bullet }$
onto the generic point.
Proof of Lemma 3.24.
From now on we replace
![]() $X$
by
$X$
by
![]() $U$
without loss of generality. Recall that the co-simplicial algebra
$U$
without loss of generality. Recall that the co-simplicial algebra
 $\mathsf{A}_{X,|Z|}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
is a subobject of the co-simplicial algebra
$\mathsf{A}_{X,|Z|}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
is a subobject of the co-simplicial algebra
 $$\begin{eqnarray}[n]\mapsto \mathop{\prod }_{[n]\rightarrow |Z|_{{\leqslant}}}\mathsf{A}_{X,\unicode[STIX]{x1D70E}}({\mathcal{O}}_{\unicode[STIX]{x1D702}})\end{eqnarray}$$
$$\begin{eqnarray}[n]\mapsto \mathop{\prod }_{[n]\rightarrow |Z|_{{\leqslant}}}\mathsf{A}_{X,\unicode[STIX]{x1D70E}}({\mathcal{O}}_{\unicode[STIX]{x1D702}})\end{eqnarray}$$
(Lemma 1.8). For
 $\unicode[STIX]{x1D70E}:[n]\rightarrow |Z|_{{\leqslant}}$
we denote by
$\unicode[STIX]{x1D70E}:[n]\rightarrow |Z|_{{\leqslant}}$
we denote by
![]() $\unicode[STIX]{x1D70E}_{+}$
the map
$\unicode[STIX]{x1D70E}_{+}$
the map
 $[n+1]\rightarrow |Z|_{{\leqslant}}$
, which restricts to
$[n+1]\rightarrow |Z|_{{\leqslant}}$
, which restricts to
![]() $\unicode[STIX]{x1D70E}$
along the map
$\unicode[STIX]{x1D70E}$
along the map
 $[n]\rightarrow [n+1]$
, and sends
$[n]\rightarrow [n+1]$
, and sends
![]() $n+1$
to
$n+1$
to
![]() $\unicode[STIX]{x1D702}$
. By definition, we have
$\unicode[STIX]{x1D702}$
. By definition, we have
 $\mathsf{A}_{X,\unicode[STIX]{x1D70E}}({\mathcal{O}}_{\unicode[STIX]{x1D702}})=\mathsf{A}_{X,\unicode[STIX]{x1D70E}_{+}}({\mathcal{O}}_{X})$
. Therefore, we have for
$\mathsf{A}_{X,\unicode[STIX]{x1D70E}}({\mathcal{O}}_{\unicode[STIX]{x1D702}})=\mathsf{A}_{X,\unicode[STIX]{x1D70E}_{+}}({\mathcal{O}}_{X})$
. Therefore, we have for
 $\unicode[STIX]{x1D6FC}:[n]\rightarrow [1]$
that the chain of points corresponding to
$\unicode[STIX]{x1D6FC}:[n]\rightarrow [1]$
that the chain of points corresponding to
 $h_{n,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E})_{+}$
can be extended to the chain
$h_{n,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E})_{+}$
can be extended to the chain
![]() $\unicode[STIX]{x1D70E}_{+}$
, that is, there is a canonical inclusion
$\unicode[STIX]{x1D70E}_{+}$
, that is, there is a canonical inclusion
 $$\begin{eqnarray}i_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FC}}:\mathsf{A}_{X,h_{n,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E})}({\mathcal{O}}_{\unicode[STIX]{x1D702}})\rightarrow \mathsf{A}_{X,\unicode[STIX]{x1D70E}}({\mathcal{O}}_{\unicode[STIX]{x1D702}}).\end{eqnarray}$$
$$\begin{eqnarray}i_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FC}}:\mathsf{A}_{X,h_{n,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E})}({\mathcal{O}}_{\unicode[STIX]{x1D702}})\rightarrow \mathsf{A}_{X,\unicode[STIX]{x1D70E}}({\mathcal{O}}_{\unicode[STIX]{x1D702}}).\end{eqnarray}$$
We define the homotopy as a map
 $$\begin{eqnarray}h^{n,\unicode[STIX]{x1D6FC}}:\mathop{\prod }_{\unicode[STIX]{x1D70E}:[n]\rightarrow |Z|_{{\leqslant}}}\mathsf{A}_{X,\unicode[STIX]{x1D70E}}({\mathcal{O}}_{\unicode[STIX]{x1D702}})\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D70E}:[n]\rightarrow |Z|_{{\leqslant}}}\mathsf{A}_{X,\unicode[STIX]{x1D70E}}({\mathcal{O}}_{\unicode[STIX]{x1D702}}),\end{eqnarray}$$
$$\begin{eqnarray}h^{n,\unicode[STIX]{x1D6FC}}:\mathop{\prod }_{\unicode[STIX]{x1D70E}:[n]\rightarrow |Z|_{{\leqslant}}}\mathsf{A}_{X,\unicode[STIX]{x1D70E}}({\mathcal{O}}_{\unicode[STIX]{x1D702}})\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D70E}:[n]\rightarrow |Z|_{{\leqslant}}}\mathsf{A}_{X,\unicode[STIX]{x1D70E}}({\mathcal{O}}_{\unicode[STIX]{x1D702}}),\end{eqnarray}$$
sending
 $(x_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}:[n]\rightarrow |Z|_{{\leqslant}}}$
to
$(x_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}:[n]\rightarrow |Z|_{{\leqslant}}}$
to
 $(i_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FC}}(x_{h_{n,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E})}))_{\unicode[STIX]{x1D70E}:[n]\rightarrow |Z|_{{\leqslant}}}$
. It remains to verify that the homotopy
$(i_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FC}}(x_{h_{n,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E})}))_{\unicode[STIX]{x1D70E}:[n]\rightarrow |Z|_{{\leqslant}}}$
. It remains to verify that the homotopy
![]() $h^{n,\unicode[STIX]{x1D6FC}}$
respects the subobject
$h^{n,\unicode[STIX]{x1D6FC}}$
respects the subobject
 $\mathsf{A}_{X,|Z|}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
.
$\mathsf{A}_{X,|Z|}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
.
To see this for a given
 $\unicode[STIX]{x1D6FC}:[n]\rightarrow [1]$
, we observe that the ring homomorphism
$\unicode[STIX]{x1D6FC}:[n]\rightarrow [1]$
, we observe that the ring homomorphism
 $h^{n,\unicode[STIX]{x1D6FC}}:\mathsf{A}_{X}^{n}({\mathcal{O}}_{\unicode[STIX]{x1D702}})\rightarrow \mathsf{A}_{X}^{n}({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
can be obtained using the co-simplicial structure
$h^{n,\unicode[STIX]{x1D6FC}}:\mathsf{A}_{X}^{n}({\mathcal{O}}_{\unicode[STIX]{x1D702}})\rightarrow \mathsf{A}_{X}^{n}({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
can be obtained using the co-simplicial structure
 $\mathsf{A}_{X}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
. For
$\mathsf{A}_{X}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
. For
 $\unicode[STIX]{x1D6FC}:[n]\rightarrow [1]$
, we denote by
$\unicode[STIX]{x1D6FC}:[n]\rightarrow [1]$
, we denote by
 $[k]=\unicode[STIX]{x1D6FC}^{-1}(0)_{+}$
the preimage of
$[k]=\unicode[STIX]{x1D6FC}^{-1}(0)_{+}$
the preimage of
![]() $0$
, with an additional maximal element
$0$
, with an additional maximal element
![]() $\unicode[STIX]{x1D702}$
adjoined (otherwise
$\unicode[STIX]{x1D702}$
adjoined (otherwise
![]() $k$
could be empty). We let
$k$
could be empty). We let
 $s:[k]\rightarrow [n]_{+}$
be the inclusion, which identifies
$s:[k]\rightarrow [n]_{+}$
be the inclusion, which identifies
![]() $[k]\setminus \{\unicode[STIX]{x1D702}\}$
with
$[k]\setminus \{\unicode[STIX]{x1D702}\}$
with
![]() $\unicode[STIX]{x1D6FC}^{-1}(0)$
, and preserves maxima. We define
$\unicode[STIX]{x1D6FC}^{-1}(0)$
, and preserves maxima. We define
 $r:[n]_{+}\rightarrow [k]$
to be the unique map in
$r:[n]_{+}\rightarrow [k]$
to be the unique map in
![]() $\unicode[STIX]{x1D6E5}$
, preserving maxima, and satisfying
$\unicode[STIX]{x1D6E5}$
, preserving maxima, and satisfying
 $r\circ s=\operatorname{id}_{[k]}$
. We let
$r\circ s=\operatorname{id}_{[k]}$
. We let
 $p=s\circ r:[n]_{+}\rightarrow [n]_{+}$
, and define
$p=s\circ r:[n]_{+}\rightarrow [n]_{+}$
, and define
 $T=\{(x_{0}\leqslant \cdots \leqslant x_{n+1}\in |X|_{n+1}|x_{n+1}=\unicode[STIX]{x1D702})\}$
. By virtue of [Reference HuberHub91, §§ 2.2 and 2.3] we have a morphism
$T=\{(x_{0}\leqslant \cdots \leqslant x_{n+1}\in |X|_{n+1}|x_{n+1}=\unicode[STIX]{x1D702})\}$
. By virtue of [Reference HuberHub91, §§ 2.2 and 2.3] we have a morphism
 $\mathsf{A}_{X}^{n}({\mathcal{O}}_{\unicode[STIX]{x1D702}})=\mathsf{A}_{X,T}^{n+1}({\mathcal{O}}_{X})\rightarrow \mathsf{A}_{X,T}^{n+1}({\mathcal{O}}_{X})=\mathsf{A}_{X}^{n}({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
, which agrees with
$\mathsf{A}_{X}^{n}({\mathcal{O}}_{\unicode[STIX]{x1D702}})=\mathsf{A}_{X,T}^{n+1}({\mathcal{O}}_{X})\rightarrow \mathsf{A}_{X,T}^{n+1}({\mathcal{O}}_{X})=\mathsf{A}_{X}^{n}({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
, which agrees with
![]() $h^{n,\unicode[STIX]{x1D6FC}}$
on the local factors. This shows that the homotopies
$h^{n,\unicode[STIX]{x1D6FC}}$
on the local factors. This shows that the homotopies
![]() $h^{n,\unicode[STIX]{x1D6FC}}$
are well-defined.
$h^{n,\unicode[STIX]{x1D6FC}}$
are well-defined.
Hence, we have constructed a homotopy between
 $\operatorname{id}_{\mathsf{A}_{X,|Z|}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})}$
and the composition
$\operatorname{id}_{\mathsf{A}_{X,|Z|}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})}$
and the composition
 $$\begin{eqnarray}\mathsf{A}_{X,|Z|}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})\rightarrow (\widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}})^{\bullet }\rightarrow \mathsf{A}_{X,|Z|}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{A}_{X,|Z|}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})\rightarrow (\widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}})^{\bullet }\rightarrow \mathsf{A}_{X,|Z|}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}}).\end{eqnarray}$$
This concludes the proof. ◻
Since homotopy equivalent co-simplicial rings have equivalent categories of cartesian modules by Lemma A.9, we obtain the following consequence.
Corollary 3.25. For
![]() $X$
an affine Noetherian scheme, with a closed subset
$X$
an affine Noetherian scheme, with a closed subset
 $|Z|\subset X$
, and
$|Z|\subset X$
, and
 $M^{\bullet }\in |\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|$
(that is,
$M^{\bullet }\in |\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|$
(that is,
 $M^{\bullet }|_{X\setminus |Z|}\simeq 0$
, see also Lemma 3.14), for every generic point
$M^{\bullet }|_{X\setminus |Z|}\simeq 0$
, see also Lemma 3.14), for every generic point
![]() $\unicode[STIX]{x1D702}$
of
$\unicode[STIX]{x1D702}$
of
![]() $|Z|$
, the stalk
$|Z|$
, the stalk
 $(\int M^{\bullet })_{\unicode[STIX]{x1D702}}$
is a perfect
$(\int M^{\bullet })_{\unicode[STIX]{x1D702}}$
is a perfect
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D702}}$
-complex.
${\mathcal{O}}_{\unicode[STIX]{x1D702}}$
-complex.
Proof. By the projection formula (Lemma 3.11) we have
 $(\int M^{\bullet })_{\unicode[STIX]{x1D702}}\simeq \int (M^{\bullet }\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{\unicode[STIX]{x1D702}})$
. The co-simplicial object
$(\int M^{\bullet })_{\unicode[STIX]{x1D702}}\simeq \int (M^{\bullet }\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{\unicode[STIX]{x1D702}})$
. The co-simplicial object
 $M^{\bullet }\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}$
can be viewed as an
$M^{\bullet }\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}$
can be viewed as an
 $\mathsf{A}_{X,|Z|_{\bullet }}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
-module by Lemma 3.14. Since the co-simplicial sheaf of algebras
$\mathsf{A}_{X,|Z|_{\bullet }}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
-module by Lemma 3.14. Since the co-simplicial sheaf of algebras
 $\mathsf{A}_{X,|Z|_{\bullet }}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
is homotopy equivalent to the constant co-simplicial sheaf of algebras
$\mathsf{A}_{X,|Z|_{\bullet }}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
is homotopy equivalent to the constant co-simplicial sheaf of algebras
![]() $\widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}}$
, with homotopy inverse given by the projection
$\widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}}$
, with homotopy inverse given by the projection
 $\mathsf{A}_{X,|Z|_{\bullet }}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})\rightarrow \widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}}$
, we have an equivalence
$\mathsf{A}_{X,|Z|_{\bullet }}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})\rightarrow \widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}}$
, we have an equivalence
 $$\begin{eqnarray}|\mathsf{Perf}(\mathsf{A}_{X,|Z|_{\bullet }}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}}))|\rightarrow \mathsf{Perf}(\widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}}),\end{eqnarray}$$
$$\begin{eqnarray}|\mathsf{Perf}(\mathsf{A}_{X,|Z|_{\bullet }}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}}))|\rightarrow \mathsf{Perf}(\widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}}),\end{eqnarray}$$
inverse to the realisation functor given by tensoring along
 $\mathsf{A}_{X,|Z|_{\bullet }}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})\rightarrow \widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}}$
. By Corollary 3.15 we have an equivalence of functors
$\mathsf{A}_{X,|Z|_{\bullet }}^{\bullet }({\mathcal{O}}_{\unicode[STIX]{x1D702}})\rightarrow \widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}}$
. By Corollary 3.15 we have an equivalence of functors
 $$\begin{eqnarray}\int _{X,|Z|}~\circ ~(-\otimes _{\mathsf{A}_{X}^{\bullet }}\mathsf{A}_{X,|Z|}^{\bullet })\simeq \int _{X}:|\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|\rightarrow \mathsf{QC}_{|Z|}(X).\end{eqnarray}$$
$$\begin{eqnarray}\int _{X,|Z|}~\circ ~(-\otimes _{\mathsf{A}_{X}^{\bullet }}\mathsf{A}_{X,|Z|}^{\bullet })\simeq \int _{X}:|\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|\rightarrow \mathsf{QC}_{|Z|}(X).\end{eqnarray}$$
This implies that
 $(\int M^{\bullet })_{\unicode[STIX]{x1D702}}$
is a perfect
$(\int M^{\bullet })_{\unicode[STIX]{x1D702}}$
is a perfect
![]() $\widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}}$
-complex. Therefore, we see that the equivalence of (5) restricted to the full subcategory
$\widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}}$
-complex. Therefore, we see that the equivalence of (5) restricted to the full subcategory
 $\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })$
lands in
$\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })$
lands in
 $\mathsf{Perf}_{\{\unicode[STIX]{x1D702}\}}(\widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}})$
. In Theorem 3.19, we have recorded the result of Thomason–Trobaugh that this category is equivalent to
$\mathsf{Perf}_{\{\unicode[STIX]{x1D702}\}}(\widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}})$
. In Theorem 3.19, we have recorded the result of Thomason–Trobaugh that this category is equivalent to
 $\mathsf{Perf}_{\{\unicode[STIX]{x1D702}\}}({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
. This shows that
$\mathsf{Perf}_{\{\unicode[STIX]{x1D702}\}}({\mathcal{O}}_{\unicode[STIX]{x1D702}})$
. This shows that
 $(\int M^{\bullet })_{\unicode[STIX]{x1D702}}$
is a perfect complex of
$(\int M^{\bullet })_{\unicode[STIX]{x1D702}}$
is a perfect complex of
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D702}}$
-modules.◻
${\mathcal{O}}_{\unicode[STIX]{x1D702}}$
-modules.◻
Lemma 3.26. Let
![]() $X$
be an affine Noetherian scheme,
$X$
be an affine Noetherian scheme,
 $|Z|\subset X$
a closed subset and
$|Z|\subset X$
a closed subset and
 $M^{\bullet }\in |\mathsf{Perf}(\mathsf{A}_{X,|Z|_{\bullet }}^{\bullet })|$
, such that for
$M^{\bullet }\in |\mathsf{Perf}(\mathsf{A}_{X,|Z|_{\bullet }}^{\bullet })|$
, such that for
![]() $\unicode[STIX]{x1D702}$
a generic point of
$\unicode[STIX]{x1D702}$
a generic point of
![]() $|Z|$
, we have
$|Z|$
, we have
 $M^{0}\otimes _{\mathsf{A}_{X,|Z|}^{0}}\widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}}\simeq 0$
. Then, there exists an open neighbourhood
$M^{0}\otimes _{\mathsf{A}_{X,|Z|}^{0}}\widehat{{\mathcal{O}}}_{\unicode[STIX]{x1D702}}\simeq 0$
. Then, there exists an open neighbourhood
![]() $V\subset X$
of
$V\subset X$
of
![]() $\unicode[STIX]{x1D702}$
, such that
$\unicode[STIX]{x1D702}$
, such that
 $M^{\bullet }|_{V}\simeq 0$
.
$M^{\bullet }|_{V}\simeq 0$
.
Proof. We begin by discussing the special case
 $|X|=|Z|$
to which we will eventually reduce the general case.
$|X|=|Z|$
to which we will eventually reduce the general case.
Let
 $\mathsf{A}_{X,<\unicode[STIX]{x1D702}}^{0}=\prod _{x<\unicode[STIX]{x1D702}}\widehat{{\mathcal{O}}}_{x}$
, which is a factor of
$\mathsf{A}_{X,<\unicode[STIX]{x1D702}}^{0}=\prod _{x<\unicode[STIX]{x1D702}}\widehat{{\mathcal{O}}}_{x}$
, which is a factor of
 $\mathsf{A}_{X}^{0}=\prod _{x\in |X|}\widehat{{\mathcal{O}}}_{x}$
. By assumption,
$\mathsf{A}_{X}^{0}=\prod _{x\in |X|}\widehat{{\mathcal{O}}}_{x}$
. By assumption,
 $\mathsf{A}_{X,<\unicode[STIX]{x1D702}}^{0}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}$
is a factor of
$\mathsf{A}_{X,<\unicode[STIX]{x1D702}}^{0}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}$
is a factor of
![]() $\mathsf{A}_{X}^{1}$
. Via the co-simplicial structure, the second ring receives a map from
$\mathsf{A}_{X}^{1}$
. Via the co-simplicial structure, the second ring receives a map from
![]() $\mathsf{A}_{X,<\unicode[STIX]{x1D702}}^{0}$
and also from
$\mathsf{A}_{X,<\unicode[STIX]{x1D702}}^{0}$
and also from
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D702}}$
(another factor of
${\mathcal{O}}_{\unicode[STIX]{x1D702}}$
(another factor of
![]() $\mathsf{A}_{X}^{0}$
):
$\mathsf{A}_{X}^{0}$
):

The assumption
 $M^{0}\otimes _{\mathsf{A}_{X}^{0}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}\simeq 0$
implies therefore also
$M^{0}\otimes _{\mathsf{A}_{X}^{0}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}\simeq 0$
implies therefore also
 $M^{1}\otimes _{\mathsf{A}_{X}^{1}}(\mathsf{A}_{X,<\unicode[STIX]{x1D702}}^{0}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{\unicode[STIX]{x1D702}})\simeq 0$
.
$M^{1}\otimes _{\mathsf{A}_{X}^{1}}(\mathsf{A}_{X,<\unicode[STIX]{x1D702}}^{0}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{\unicode[STIX]{x1D702}})\simeq 0$
.
Using that
 $M^{\bullet }\in |\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|$
is a cartesian co-simplicial perfect complex, we see that
$M^{\bullet }\in |\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|$
is a cartesian co-simplicial perfect complex, we see that
 $$\begin{eqnarray}0\simeq M^{0}\otimes _{\mathsf{A}_{X}^{0}}(\mathsf{A}_{X,<\unicode[STIX]{x1D702}}^{0}\otimes {\mathcal{O}}_{\unicode[STIX]{x1D702}})\simeq M^{0}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{\unicode[STIX]{x1D702}},\end{eqnarray}$$
$$\begin{eqnarray}0\simeq M^{0}\otimes _{\mathsf{A}_{X}^{0}}(\mathsf{A}_{X,<\unicode[STIX]{x1D702}}^{0}\otimes {\mathcal{O}}_{\unicode[STIX]{x1D702}})\simeq M^{0}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{\unicode[STIX]{x1D702}},\end{eqnarray}$$
where we have used that
 $M^{0}\otimes _{\mathsf{A}_{X}^{0}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}\simeq 0$
.
$M^{0}\otimes _{\mathsf{A}_{X}^{0}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}\simeq 0$
.
We can write
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D702}}$
as a filtered colimit of rings
${\mathcal{O}}_{\unicode[STIX]{x1D702}}$
as a filtered colimit of rings
 $\mathsf{colim}_{f\in {\mathcal{O}}_{X}}{\mathcal{O}}_{X,f}$
, and hence see that
$\mathsf{colim}_{f\in {\mathcal{O}}_{X}}{\mathcal{O}}_{X,f}$
, and hence see that
 $$\begin{eqnarray}\mathsf{A}_{X,|Z|,<\unicode[STIX]{x1D702}}^{0}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}\simeq \mathsf{colim}_{f\in {\mathcal{O}}_{X}}\mathsf{A}_{X,|Z|,<\unicode[STIX]{x1D702}}^{0}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{X,f}\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{A}_{X,|Z|,<\unicode[STIX]{x1D702}}^{0}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}\simeq \mathsf{colim}_{f\in {\mathcal{O}}_{X}}\mathsf{A}_{X,|Z|,<\unicode[STIX]{x1D702}}^{0}\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{X,f}\end{eqnarray}$$
is a filtered colimit of rings.
By [Reference Thomason and TrobaughTT90, Proposition 3.20], if
 $R=\mathsf{colim}_{i\in I}R_{i}$
is a filtered colimit of rings, and for
$R=\mathsf{colim}_{i\in I}R_{i}$
is a filtered colimit of rings, and for
![]() $j\in I$
,
$j\in I$
,
 $M_{j}\in \mathsf{Perf}(R_{j})$
, such that
$M_{j}\in \mathsf{Perf}(R_{j})$
, such that
 $M_{j}\otimes _{R_{j}}R\simeq 0$
, then there exists
$M_{j}\otimes _{R_{j}}R\simeq 0$
, then there exists
![]() $i\geqslant j$
, such that
$i\geqslant j$
, such that
 $M_{j}\otimes _{R_{j}}R_{i}\simeq 0$
(in [Reference Thomason and TrobaughTT90] it is shown that the homotopy category of perfect complexes of
$M_{j}\otimes _{R_{j}}R_{i}\simeq 0$
(in [Reference Thomason and TrobaughTT90] it is shown that the homotopy category of perfect complexes of
![]() $R$
-modules is equivalent to the filtered colimit of the homotopy category of perfect complexes of
$R$
-modules is equivalent to the filtered colimit of the homotopy category of perfect complexes of
![]() $R_{i}$
-modules).
$R_{i}$
-modules).
Since our sheaves of algebras are lâche, we may apply this result, since by virtue of Corollary 2.23 the categories over perfect complexes over these sheaves of algebras are equivalent to perfect complexes over the rings of global sections. Hence, we see that there exists
 $f\in {\mathcal{O}}_{X}$
, such that
$f\in {\mathcal{O}}_{X}$
, such that
 $(M^{0}\otimes _{\mathsf{A}_{X}^{0}}\mathsf{A}_{X,<\unicode[STIX]{x1D702}}^{0})\otimes {\mathcal{O}}_{f}\simeq 0$
. Restricting both sides to the open subset
$(M^{0}\otimes _{\mathsf{A}_{X}^{0}}\mathsf{A}_{X,<\unicode[STIX]{x1D702}}^{0})\otimes {\mathcal{O}}_{f}\simeq 0$
. Restricting both sides to the open subset
![]() $V\subset X$
defined by localisation at
$V\subset X$
defined by localisation at
![]() $f$
, we obtain
$f$
, we obtain
 $M^{0}|_{V}\simeq 0$
, because
$M^{0}|_{V}\simeq 0$
, because
 $({\mathcal{O}}_{f})|_{V}\simeq {\mathcal{O}}$
. This concludes the proof of the case
$({\mathcal{O}}_{f})|_{V}\simeq {\mathcal{O}}$
. This concludes the proof of the case
 $|X|=|Z|$
.
$|X|=|Z|$
.
Let
 $i:Z{\hookrightarrow}X$
be a closed immersion, such that its underlying closed subset is the one of interest
$i:Z{\hookrightarrow}X$
be a closed immersion, such that its underlying closed subset is the one of interest
![]() $|Z|$
. By Lemma 1.11 we have a canonical map
$|Z|$
. By Lemma 1.11 we have a canonical map
 $\mathsf{A}_{X,|Z|}^{\bullet }\rightarrow i_{\ast }\mathsf{A}_{Z}^{\bullet }$
. Tensoring along this map produces a functor
$\mathsf{A}_{X,|Z|}^{\bullet }\rightarrow i_{\ast }\mathsf{A}_{Z}^{\bullet }$
. Tensoring along this map produces a functor
 $|\mathsf{Perf}(\mathsf{A}_{X,|Z|}^{\bullet })|\rightarrow |\mathsf{Perf}(\mathsf{A}_{Z}^{\bullet })|$
.
$|\mathsf{Perf}(\mathsf{A}_{X,|Z|}^{\bullet })|\rightarrow |\mathsf{Perf}(\mathsf{A}_{Z}^{\bullet })|$
.
For any
![]() $M^{\bullet }$
in
$M^{\bullet }$
in
 $|\mathsf{Perf}(\mathsf{A}_{X,|Z|}^{\bullet })|$
, such that
$|\mathsf{Perf}(\mathsf{A}_{X,|Z|}^{\bullet })|$
, such that
 $M^{0}\otimes _{\mathsf{A}_{X,|Z|}^{\bullet }}\widehat{{\mathcal{O}}}_{X,\unicode[STIX]{x1D702}}\simeq 0$
, we obtain therefore by functoriality
$M^{0}\otimes _{\mathsf{A}_{X,|Z|}^{\bullet }}\widehat{{\mathcal{O}}}_{X,\unicode[STIX]{x1D702}}\simeq 0$
, we obtain therefore by functoriality
 $N^{\bullet }=M^{\bullet }\otimes _{\mathsf{A}_{X,|Z|}^{\bullet }}\mathsf{A}_{X}^{\bullet }$
, which also satisfies vanishing at the generic point. Our treatment of the special case
$N^{\bullet }=M^{\bullet }\otimes _{\mathsf{A}_{X,|Z|}^{\bullet }}\mathsf{A}_{X}^{\bullet }$
, which also satisfies vanishing at the generic point. Our treatment of the special case
 $|X|=|Z|$
can therefore be applied to
$|X|=|Z|$
can therefore be applied to
![]() $Z$
, and we obtain an open subscheme
$Z$
, and we obtain an open subscheme
![]() $U\subset Z$
, such that for every
$U\subset Z$
, such that for every
![]() $x\in U$
we have
$x\in U$
we have
 $N^{0}\otimes _{\mathsf{A}_{X}^{\bullet }}\widehat{{\mathcal{O}}}_{Z,x}\simeq 0$
.
$N^{0}\otimes _{\mathsf{A}_{X}^{\bullet }}\widehat{{\mathcal{O}}}_{Z,x}\simeq 0$
.
To conclude the proof it remains to show that we also have
 $M^{0}\otimes _{\mathsf{A}_{X,|Z|}^{\bullet }}\widehat{{\mathcal{O}}}_{X,x}\simeq 0$
for every
$M^{0}\otimes _{\mathsf{A}_{X,|Z|}^{\bullet }}\widehat{{\mathcal{O}}}_{X,x}\simeq 0$
for every
![]() $x\in U$
. This is simply a consequence of Nakayama’s lemma: the map
$x\in U$
. This is simply a consequence of Nakayama’s lemma: the map
 $\widehat{{\mathcal{O}}}_{X,x}\rightarrow \widehat{{\mathcal{O}}}_{Z,x}$
is a morphism of local rings inducing an isomorphism of residue field. Since a perfect complex over a local ring is acyclic if and only if it is acyclic over the residue fields, this concludes the proof.◻
$\widehat{{\mathcal{O}}}_{X,x}\rightarrow \widehat{{\mathcal{O}}}_{Z,x}$
is a morphism of local rings inducing an isomorphism of residue field. Since a perfect complex over a local ring is acyclic if and only if it is acyclic over the residue fields, this concludes the proof.◻
The following non-example demonstrates how the property of being 0 at the generic point spreads out to an open neighbourhood.
Example 3.27. Consider the example
 $X=\operatorname{Spec}\mathbb{Z}$
, we then have a perfect
$X=\operatorname{Spec}\mathbb{Z}$
, we then have a perfect
![]() $\mathbb{A}_{X}^{0}$
-complex given by
$\mathbb{A}_{X}^{0}$
-complex given by
 $0\times \prod _{p\text{ prime}}\mathbb{F}_{p}$
by Bhatt’s Theorem 3.16 for perfect complexes over product rings. Here the factor 0 reminds us that the
$0\times \prod _{p\text{ prime}}\mathbb{F}_{p}$
by Bhatt’s Theorem 3.16 for perfect complexes over product rings. Here the factor 0 reminds us that the
![]() $\mathbb{Q}$
-factor of
$\mathbb{Q}$
-factor of
![]() $\mathbb{A}_{X}^{0}$
acts trivially the product. We claim that this perfect complex cannot be
$\mathbb{A}_{X}^{0}$
acts trivially the product. We claim that this perfect complex cannot be
![]() $M^{0}$
of an adelic descent datum
$M^{0}$
of an adelic descent datum
 $M^{\bullet }\in |\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|$
. Indeed, if it was, then we would have
$M^{\bullet }\in |\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|$
. Indeed, if it was, then we would have
 $M^{0}\otimes _{\mathbb{A}_{X}^{0}}\mathbb{Q}\simeq 0$
, as can be seen by tensoring
$M^{0}\otimes _{\mathbb{A}_{X}^{0}}\mathbb{Q}\simeq 0$
, as can be seen by tensoring
![]() $M^{0}$
with the ring homomorphism given by the composition
$M^{0}$
with the ring homomorphism given by the composition
 $\mathbb{A}_{X}^{0}\rightarrow \mathbb{Q}\rightarrow \mathbb{A}_{X}^{1}$
, which corresponds to one of the face maps. By construction,
$\mathbb{A}_{X}^{0}\rightarrow \mathbb{Q}\rightarrow \mathbb{A}_{X}^{1}$
, which corresponds to one of the face maps. By construction,
 $M^{0}\otimes _{\mathbb{A}_{X}^{0}}\mathbb{Q}$
is already 0. However, there is a second face map
$M^{0}\otimes _{\mathbb{A}_{X}^{0}}\mathbb{Q}$
is already 0. However, there is a second face map
 $\mathbb{A}_{X}^{0}\rightarrow \mathbb{A}_{X}^{1}$
, which agrees with the natural map
$\mathbb{A}_{X}^{0}\rightarrow \mathbb{A}_{X}^{1}$
, which agrees with the natural map
 $(\mathbb{A}_{X}^{0}\rightarrow \mathbb{A}_{X}^{1}\otimes \mathbb{Q})$
away from the degenerate part of
$(\mathbb{A}_{X}^{0}\rightarrow \mathbb{A}_{X}^{1}\otimes \mathbb{Q})$
away from the degenerate part of
![]() $\mathbb{A}_{X}^{1}$
. Since tensoring along the face maps should produce quasi-isomorphic perfect complexes, we see that
$\mathbb{A}_{X}^{1}$
. Since tensoring along the face maps should produce quasi-isomorphic perfect complexes, we see that
 $M^{0}\otimes \mathbb{Q}\simeq 0$
. However, the element
$M^{0}\otimes \mathbb{Q}\simeq 0$
. However, the element
 $(1,\ldots )_{p~\text{prime}}\in {\mathcal{H}}^{0}(M^{0})$
is not annihilated by any
$(1,\ldots )_{p~\text{prime}}\in {\mathcal{H}}^{0}(M^{0})$
is not annihilated by any
 $f\in {\mathcal{O}}_{X}(X)=\mathbb{Z}$
.
$f\in {\mathcal{O}}_{X}(X)=\mathbb{Z}$
.
We will now put this spreading-out property of adelic descent data to use, to show that for
 $M\in |\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|$
the complex
$M\in |\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|$
the complex
![]() $\int M$
is generically perfect.
$\int M$
is generically perfect.
Corollary 3.28. Let
![]() $X$
be an affine Noetherian scheme, let
$X$
be an affine Noetherian scheme, let
 $|Z|\subset X$
be a closed subset and let
$|Z|\subset X$
be a closed subset and let
 $M^{\bullet }\in |\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|$
. For every generic point
$M^{\bullet }\in |\mathsf{Perf}_{|Z|}(\mathsf{A}_{X}^{\bullet })|$
. For every generic point
![]() $\unicode[STIX]{x1D702}$
of
$\unicode[STIX]{x1D702}$
of
![]() $|Z|$
exists an open neighbourhood
$|Z|$
exists an open neighbourhood
![]() $U\subset X$
, such that
$U\subset X$
, such that
 $(\int M^{\bullet })|_{U}$
is a perfect complex on
$(\int M^{\bullet })|_{U}$
is a perfect complex on
![]() $U$
.
$U$
.
Proof. Choose an isomorphism of
 $(\int M^{\bullet })\rightarrow \mathsf{colim}_{i\in I}N_{i}$
with a filtered colimit of perfect complexes on
$(\int M^{\bullet })\rightarrow \mathsf{colim}_{i\in I}N_{i}$
with a filtered colimit of perfect complexes on
![]() $X$
. By Corollary 3.25, we know that
$X$
. By Corollary 3.25, we know that
 $(\int M^{\bullet })_{\unicode[STIX]{x1D702}}$
is a perfect
$(\int M^{\bullet })_{\unicode[STIX]{x1D702}}$
is a perfect
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D702}}$
-complex. Therefore, we see that there exists an index
${\mathcal{O}}_{\unicode[STIX]{x1D702}}$
-complex. Therefore, we see that there exists an index
![]() $j\in I$
, such that we have a factorisation
$j\in I$
, such that we have a factorisation

and we see that
 $p=s\circ r$
defines an idempotent on
$p=s\circ r$
defines an idempotent on
![]() $(N_{j})_{\unicode[STIX]{x1D702}}$
, such that the corresponding direct summand is equivalent to
$(N_{j})_{\unicode[STIX]{x1D702}}$
, such that the corresponding direct summand is equivalent to
 $(\int M^{\bullet })_{\unicode[STIX]{x1D702}}$
. Since
$(\int M^{\bullet })_{\unicode[STIX]{x1D702}}$
. Since
![]() $N_{j}$
is perfect, there exists an affine open subset
$N_{j}$
is perfect, there exists an affine open subset
![]() $U\subset X$
, and an idempotent
$U\subset X$
, and an idempotent
![]() $p$
on
$p$
on
![]() $N_{j}|_{U}$
, which extends the one over
$N_{j}|_{U}$
, which extends the one over
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D702}}$
. Passing to the corresponding direct summand
${\mathcal{O}}_{\unicode[STIX]{x1D702}}$
. Passing to the corresponding direct summand
![]() $N_{j}^{\prime }$
of
$N_{j}^{\prime }$
of
![]() $N_{j}|_{U}$
, we see that we have constructed a direct summand
$N_{j}|_{U}$
, we see that we have constructed a direct summand
![]() $N_{j}^{\prime }$
, with a map to
$N_{j}^{\prime }$
, with a map to
 $(\int M^{\bullet })|_{U}$
, which induces an equivalence at
$(\int M^{\bullet })|_{U}$
, which induces an equivalence at
![]() $\unicode[STIX]{x1D702}$
. By adjunction, we have a morphism
$\unicode[STIX]{x1D702}$
. By adjunction, we have a morphism
 $N_{j}^{\prime }\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X,|Z|}^{\bullet }\rightarrow M^{\bullet }$
, which is an equivalence after tensoring with
$N_{j}^{\prime }\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X,|Z|}^{\bullet }\rightarrow M^{\bullet }$
, which is an equivalence after tensoring with
 $-\otimes _{\mathsf{A}_{X,|Z|}^{0}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}$
. By Lemma 3.26 there exists an open subset
$-\otimes _{\mathsf{A}_{X,|Z|}^{0}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}$
. By Lemma 3.26 there exists an open subset
![]() $V\subset U$
, such that
$V\subset U$
, such that
 $N_{j}^{\prime }\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{V,|Z|\cap V}^{\bullet }\rightarrow M^{\bullet }|_{V}$
is an equivalence. This implies that
$N_{j}^{\prime }\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{V,|Z|\cap V}^{\bullet }\rightarrow M^{\bullet }|_{V}$
is an equivalence. This implies that
 $(\int M^{\bullet })|_{V}$
is equivalent to
$(\int M^{\bullet })|_{V}$
is equivalent to
![]() $N_{j}^{\prime }|_{V}$
, and thus is a perfect complex.◻
$N_{j}^{\prime }|_{V}$
, and thus is a perfect complex.◻
Proof of Proposition 3.2.
As before we assume that
![]() $X$
is an affine scheme. For every adelic descent datum
$X$
is an affine scheme. For every adelic descent datum
 $M^{\bullet }\in |\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|$
, we will show that
$M^{\bullet }\in |\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })|$
, we will show that
![]() $\int M^{\bullet }$
is perfect. Thus, by conservativity of
$\int M^{\bullet }$
is perfect. Thus, by conservativity of
![]() $\int$
, and the fact that
$\int$
, and the fact that
 $-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }$
is fully faithful, we can apply Lemma A.7 to conclude the proof.
$-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }$
is fully faithful, we can apply Lemma A.7 to conclude the proof.
Let
![]() $\unicode[STIX]{x1D702}$
be a generic point of
$\unicode[STIX]{x1D702}$
be a generic point of
![]() $X$
. By virtue of Corollary 3.28 there exists an open neighbourhood
$X$
. By virtue of Corollary 3.28 there exists an open neighbourhood
![]() $U$
, and a perfect complex
$U$
, and a perfect complex
 $N\in \mathsf{Perf}(U)$
, together with an isomorphism
$N\in \mathsf{Perf}(U)$
, together with an isomorphism
 $N\otimes _{{\mathcal{O}}_{U}}\mathsf{A}_{X}^{\bullet }\simeq M|_{U}$
. After replacing
$N\otimes _{{\mathcal{O}}_{U}}\mathsf{A}_{X}^{\bullet }\simeq M|_{U}$
. After replacing
![]() $U$
by a smaller open subset, we may assume that it is a standard affine open
$U$
by a smaller open subset, we may assume that it is a standard affine open
 $U=X_{f}$
. We would like to extend this map to
$U=X_{f}$
. We would like to extend this map to
![]() $X$
, and then take the cofibre thereof. However, in general it is not possible to extend a perfect complex from an open subset, unless its
$X$
, and then take the cofibre thereof. However, in general it is not possible to extend a perfect complex from an open subset, unless its
![]() $K$
-theory class extends [Reference Thomason and TrobaughTT90, Proposition 5.2.2]. Hence, we consider instead
$K$
-theory class extends [Reference Thomason and TrobaughTT90, Proposition 5.2.2]. Hence, we consider instead
 $M_{0}^{\bullet }=M^{\bullet }\oplus \unicode[STIX]{x1D6F4}M$
, and
$M_{0}^{\bullet }=M^{\bullet }\oplus \unicode[STIX]{x1D6F4}M$
, and
 $N_{0}^{\prime }\oplus \unicode[STIX]{x1D6F4}N$
, whose
$N_{0}^{\prime }\oplus \unicode[STIX]{x1D6F4}N$
, whose
![]() $K$
-theory class is
$K$
-theory class is
![]() $0$
, but contain the perfect complexes we care about as a direct summand. We may assume that
$0$
, but contain the perfect complexes we care about as a direct summand. We may assume that
 $N_{0}^{\prime }=N_{0}^{\prime \prime }|_{U}$
, where
$N_{0}^{\prime }=N_{0}^{\prime \prime }|_{U}$
, where
 $N_{0}^{\prime \prime }\in \mathsf{Perf}(X)$
. Let
$N_{0}^{\prime \prime }\in \mathsf{Perf}(X)$
. Let
 $j:U{\hookrightarrow}X$
be the corresponding open immersion, we have a map
$j:U{\hookrightarrow}X$
be the corresponding open immersion, we have a map
 $$\begin{eqnarray}N_{0}^{\prime \prime }\rightarrow j_{\ast }j^{\ast }N_{0}^{\prime \prime }\rightarrow j_{\ast }j^{\ast }\int M_{0}^{\bullet },\end{eqnarray}$$
$$\begin{eqnarray}N_{0}^{\prime \prime }\rightarrow j_{\ast }j^{\ast }N_{0}^{\prime \prime }\rightarrow j_{\ast }j^{\ast }\int M_{0}^{\bullet },\end{eqnarray}$$
and we explain in Lemma 3.29 below there exists a line bundle
![]() $L$
, such that we have a map
$L$
, such that we have a map
 $N_{0}=N_{0}^{\prime \prime }\otimes L\rightarrow \int M_{0}^{\bullet }$
, which induces an equivalence, when restricted to
$N_{0}=N_{0}^{\prime \prime }\otimes L\rightarrow \int M_{0}^{\bullet }$
, which induces an equivalence, when restricted to
![]() $U$
. We consider the cofibre
$U$
. We consider the cofibre
![]() $C$
of the adjoint
$C$
of the adjoint
 $N_{0}\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }\rightarrow M_{0}^{\bullet }$
, and define
$N_{0}\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }\rightarrow M_{0}^{\bullet }$
, and define
 $M_{1}^{\bullet }=C\oplus \unicode[STIX]{x1D6F4}C$
.
$M_{1}^{\bullet }=C\oplus \unicode[STIX]{x1D6F4}C$
.
Since
 $M_{1}^{0}\otimes _{\mathsf{A}_{X}^{0}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}\simeq 0$
, we see that
$M_{1}^{0}\otimes _{\mathsf{A}_{X}^{0}}{\mathcal{O}}_{\unicode[STIX]{x1D702}}\simeq 0$
, we see that
 $M_{1}\in \mathsf{Perf}(\mathsf{A}_{X,|Z|}^{\bullet })$
for a closed subset
$M_{1}\in \mathsf{Perf}(\mathsf{A}_{X,|Z|}^{\bullet })$
for a closed subset
 $|Z|\subset X$
by Lemma 3.26. Iterating this process, we obtain a sequence
$|Z|\subset X$
by Lemma 3.26. Iterating this process, we obtain a sequence
 $(M_{n}^{\bullet })_{n\in \mathbb{N}}$
of objects in
$(M_{n}^{\bullet })_{n\in \mathbb{N}}$
of objects in
 $\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })$
, together with an increasing sequence of open subsets
$\mathsf{Perf}(\mathsf{A}_{X}^{\bullet })$
, together with an increasing sequence of open subsets
 $U_{n}\subset |X|$
, such that
$U_{n}\subset |X|$
, such that
 $\int M_{n}^{\bullet }|_{U_{n}}$
is perfect. Since
$\int M_{n}^{\bullet }|_{U_{n}}$
is perfect. Since
![]() $X$
is Noetherian, this sequence stabilises, that is
$X$
is Noetherian, this sequence stabilises, that is
 $U_{n}=U$
for
$U_{n}=U$
for
![]() $n\gg 0$
. We must have
$n\gg 0$
. We must have
 $U=|X|$
, because otherwise we could choose a generic point of the complement, and continue the iterative process described above. Since
$U=|X|$
, because otherwise we could choose a generic point of the complement, and continue the iterative process described above. Since
![]() $M_{n}^{\bullet }$
contains
$M_{n}^{\bullet }$
contains
![]() $M^{\bullet }$
as a direct summand, we conclude that
$M^{\bullet }$
as a direct summand, we conclude that
![]() $\int M^{\bullet }$
is a perfect complex.◻
$\int M^{\bullet }$
is a perfect complex.◻
Lemma 3.29. Let
 $X=\operatorname{Spec}R$
be an affine scheme and
$X=\operatorname{Spec}R$
be an affine scheme and
 $f\in \unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})$
a function. We follow the standard notation to denote by
$f\in \unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})$
a function. We follow the standard notation to denote by
 $U=X_{f}$
the open subset of
$U=X_{f}$
the open subset of
![]() $X$
given by the complement of the vanishing locus of
$X$
given by the complement of the vanishing locus of
![]() $f$
, and by
$f$
, and by
![]() $j$
the corresponding open inclusion. Assume that we have a perfect complex
$j$
the corresponding open inclusion. Assume that we have a perfect complex
![]() $M$
, on
$M$
, on
![]() $X$
, as well as a complex of quasi-coherent sheaves
$X$
, as well as a complex of quasi-coherent sheaves
![]() $N$
and a morphism
$N$
and a morphism
 $M\rightarrow j_{\ast }j^{\ast }N$
. Then there exists a line bundle
$M\rightarrow j_{\ast }j^{\ast }N$
. Then there exists a line bundle
![]() $L$
, which restricts to
$L$
, which restricts to
![]() ${\mathcal{O}}_{U}$
on
${\mathcal{O}}_{U}$
on
![]() $U$
, such that we have a morphism
$U$
, such that we have a morphism
 $M\otimes L\rightarrow N$
.
$M\otimes L\rightarrow N$
.
Proof. To see this we use the standard correspondence between perfect complexes on affine schemes, and perfect complexes over their rings of functions. We have an isomorphism
 ${\mathcal{O}}_{U}(U)=R_{f}\simeq \mathsf{colim}_{n\in \mathbf{N}}[R\xrightarrow[{}]{f}R\xrightarrow[{}]{f}\cdots \,]$
. Let
${\mathcal{O}}_{U}(U)=R_{f}\simeq \mathsf{colim}_{n\in \mathbf{N}}[R\xrightarrow[{}]{f}R\xrightarrow[{}]{f}\cdots \,]$
. Let
 $L^{\prime }={\mathcal{O}}_{X}$
be the trivial line bundle, and
$L^{\prime }={\mathcal{O}}_{X}$
be the trivial line bundle, and
 ${\mathcal{O}}_{X}\rightarrow L^{\prime }$
be the morphism given by multiplication with
${\mathcal{O}}_{X}\rightarrow L^{\prime }$
be the morphism given by multiplication with
![]() $f$
. We can therefore rewrite this filtered colimit by
$f$
. We can therefore rewrite this filtered colimit by
 $R_{F}\simeq \mathsf{colim}_{n\in \mathbf{N}}(L^{\prime })^{\otimes n}$
, where the transition maps are induced by the map
$R_{F}\simeq \mathsf{colim}_{n\in \mathbf{N}}(L^{\prime })^{\otimes n}$
, where the transition maps are induced by the map
 ${\mathcal{O}}_{X}\rightarrow L^{\prime }$
.
${\mathcal{O}}_{X}\rightarrow L^{\prime }$
.
Since tensor products, and thus localisation at
![]() $f$
, commute with filtered colimits, this implies that
$f$
, commute with filtered colimits, this implies that
![]() $j_{\ast }j^{\ast }N$
corresponds to the complex of
$j_{\ast }j^{\ast }N$
corresponds to the complex of
![]() $R$
-modules
$R$
-modules
 $\mathsf{colim}_{n\in \mathbf{N}}N\otimes (L^{\prime })^{\otimes n}$
. Thus, we have a map
$\mathsf{colim}_{n\in \mathbf{N}}N\otimes (L^{\prime })^{\otimes n}$
. Thus, we have a map
 $M\rightarrow \mathsf{colim}_{n\in \mathbf{N}}N\otimes (L^{\prime })^{\otimes n}$
, and since
$M\rightarrow \mathsf{colim}_{n\in \mathbf{N}}N\otimes (L^{\prime })^{\otimes n}$
, and since
![]() $M$
is perfect, and thus compact (see [Reference Thomason and TrobaughTT90, Theorem 2.4.2(e)]), we see that there exists an integer
$M$
is perfect, and thus compact (see [Reference Thomason and TrobaughTT90, Theorem 2.4.2(e)]), we see that there exists an integer
![]() $n\in \mathbf{N}$
, such that we have a factorisation
$n\in \mathbf{N}$
, such that we have a factorisation
 $M\rightarrow N\otimes (L^{\prime })^{\otimes n}\rightarrow j_{\ast }j^{\ast }N$
. The commutative diagram
$M\rightarrow N\otimes (L^{\prime })^{\otimes n}\rightarrow j_{\ast }j^{\ast }N$
. The commutative diagram

shows that for
 $L=(L^{\prime })^{\otimes -n}$
, we have a factorisation
$L=(L^{\prime })^{\otimes -n}$
, we have a factorisation
 $M\otimes L\rightarrow N\rightarrow j_{\ast }j^{\ast }N$
.◻
$M\otimes L\rightarrow N\rightarrow j_{\ast }j^{\ast }N$
.◻
3.2 Adelic reconstruction
In this subsection we collect various corollaries of our adelic descent result, Theorem 3.1. Applying the Tannakian formalism for symmetric monoidal
![]() $\infty$
-categories, we can show that a Noetherian scheme
$\infty$
-categories, we can show that a Noetherian scheme
![]() $X$
can be reconstructed from the co-simplicial ring
$X$
can be reconstructed from the co-simplicial ring
![]() $\mathbb{A}_{X}^{\bullet }$
. We will also give an adelic description of
$\mathbb{A}_{X}^{\bullet }$
. We will also give an adelic description of
![]() $G$
-torsors on
$G$
-torsors on
![]() $X$
, for any Noetherian affine group scheme, analogously to Weil’s Theorem 0.1 for algebraic curves, which inspired the present work.
$X$
, for any Noetherian affine group scheme, analogously to Weil’s Theorem 0.1 for algebraic curves, which inspired the present work.
Our results rely heavily on the Tannakian formalism for symmetric monoidal stable
![]() $\infty$
-categories, as developed by Lurie in [Reference LurieLur11], and further refined by Bhatt [Reference BhattBha16] and Bhatt and Halpern-Leistner [Reference Bhatt and Halpern-LeistnerBHL15].
$\infty$
-categories, as developed by Lurie in [Reference LurieLur11], and further refined by Bhatt [Reference BhattBha16] and Bhatt and Halpern-Leistner [Reference Bhatt and Halpern-LeistnerBHL15].
Theorem 3.30 (Bhatt–Halpern-Leistner).
(a) The category
 $\mathsf{AlgSp}^{\mathsf{qcqs}}$
of quasi-compact and quasi-separated algebraic spaces embeds fully faithfully into
$\mathsf{AlgSp}^{\mathsf{qcqs}}$
of quasi-compact and quasi-separated algebraic spaces embeds fully faithfully into
![]() $(\mathsf{st}_{\otimes })^{\mathsf{op}}$
, the dual
$(\mathsf{st}_{\otimes })^{\mathsf{op}}$
, the dual
![]() $\infty$
-category of small symmetric monoidal stable
$\infty$
-category of small symmetric monoidal stable
![]() $\infty$
-categories, by means of the functor
$\infty$
-categories, by means of the functor
 $$\begin{eqnarray}\mathsf{Perf}(-)_{\otimes }:(\mathsf{AlgSp}^{\mathsf{qcqs}})^{\mathsf{op}}{\hookrightarrow}\mathsf{st}_{\otimes }.\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Perf}(-)_{\otimes }:(\mathsf{AlgSp}^{\mathsf{qcqs}})^{\mathsf{op}}{\hookrightarrow}\mathsf{st}_{\otimes }.\end{eqnarray}$$
(b) The functor
 $\mathsf{APerf}_{\mathsf{cn}}(-)_{\otimes }$
from the
$\mathsf{APerf}_{\mathsf{cn}}(-)_{\otimes }$
from the
![]() $\infty$
-category of spectral Noetherian stacks
$\infty$
-category of spectral Noetherian stacks
 $(\mathsf{DStck}^{\mathsf{N}})^{\mathsf{op}}$
to the
$(\mathsf{DStck}^{\mathsf{N}})^{\mathsf{op}}$
to the
![]() $\infty$
-category of symmetric monoidal
$\infty$
-category of symmetric monoidal
![]() $\infty$
-categories
$\infty$
-categories
 $\infty \text{-}\mathsf{Cat}_{\otimes }$
is fully faithful.
$\infty \text{-}\mathsf{Cat}_{\otimes }$
is fully faithful.
Recall that
![]() $\mathsf{APerf}$
denotes the
$\mathsf{APerf}$
denotes the
![]() $\infty$
-category of almost perfect, that is, pseudo-coherent complexes. That is, a complex which can locally be presented as a bounded above complex of finitely generated locally projective sheaves of modules. The subscript
$\infty$
-category of almost perfect, that is, pseudo-coherent complexes. That is, a complex which can locally be presented as a bounded above complex of finitely generated locally projective sheaves of modules. The subscript
![]() $\mathsf{cn}$
refers to the full subcategory of connective objects, that is complexes which are concentrated in non-positive degrees.
$\mathsf{cn}$
refers to the full subcategory of connective objects, that is complexes which are concentrated in non-positive degrees.
3.2.1 For schemes
By a well-known theorem of Gelfand and Naimark [Reference Gelfand and NaimarkGN43], every locally compact space
![]() $X$
can be reconstructed from the ring of continuous real-valued functions. It is equally well-known that a single ring is not sufficient to capture the delicate geometry of an arbitrary non-affine scheme. The result below shows however that for a Noetherian scheme
$X$
can be reconstructed from the ring of continuous real-valued functions. It is equally well-known that a single ring is not sufficient to capture the delicate geometry of an arbitrary non-affine scheme. The result below shows however that for a Noetherian scheme
![]() $X$
, the co-simplicial ring of adèles
$X$
, the co-simplicial ring of adèles
![]() $\mathbb{A}_{X}^{\bullet }$
allows one to reconstruct
$\mathbb{A}_{X}^{\bullet }$
allows one to reconstruct
![]() $X$
. It is intriguing to observe that local compactness for topological spaces is not dissimilar from the Noetherian hypothesis for schemes. To iterate further on this philosophical point, we remind ourselves that a Banach space is finite-dimensional if and only if it is locally compact. The Noetherian condition enforces finite-dimensionality of the local rings, and guarantees that ideals are finitely generated.
$X$
. It is intriguing to observe that local compactness for topological spaces is not dissimilar from the Noetherian hypothesis for schemes. To iterate further on this philosophical point, we remind ourselves that a Banach space is finite-dimensional if and only if it is locally compact. The Noetherian condition enforces finite-dimensionality of the local rings, and guarantees that ideals are finitely generated.
Theorem 3.31. For any Noetherian scheme
![]() $X$
we have a canonical isomorphism of schemes
$X$
we have a canonical isomorphism of schemes
 $|\operatorname{Spec}\,\mathbb{A}_{X}^{\bullet }|\simeq X$
, where the colimit
$|\operatorname{Spec}\,\mathbb{A}_{X}^{\bullet }|\simeq X$
, where the colimit
![]() $|\cdot |$
is taken in the category of quasi-compact and quasi-separated schemes.
$|\cdot |$
is taken in the category of quasi-compact and quasi-separated schemes.
Proof. We use Bhatt’s Tannakian reconstruction result, as presented in [Reference BhattBha16]. Theorem 3.1 gives a symmetric monoidal equivalence
 $$\begin{eqnarray}\mathsf{Perf}(X)_{\otimes }\simeq |(\mathsf{Perf}(\mathbb{A}_{X}^{\bullet }))_{\otimes }|.\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Perf}(X)_{\otimes }\simeq |(\mathsf{Perf}(\mathbb{A}_{X}^{\bullet }))_{\otimes }|.\end{eqnarray}$$
By [Reference BhattBha16, Corollary 1.6] we may deduce the existence of an augmentation
 $\operatorname{Spec}\mathbb{A}_{X}^{\bullet }\rightarrow X$
, yielding an equivalence
$\operatorname{Spec}\mathbb{A}_{X}^{\bullet }\rightarrow X$
, yielding an equivalence
 $|\operatorname{Spec}\,\mathbb{A}_{X}^{\bullet }|\rightarrow X$
in the category of quasi-compact and quasi-separated schemes.◻
$|\operatorname{Spec}\,\mathbb{A}_{X}^{\bullet }|\rightarrow X$
in the category of quasi-compact and quasi-separated schemes.◻
Bhatt’s [Reference BhattBha16] allows one to reconstruct a quasi-compact and quasi-separated algebraic space
![]() $X$
from the symmetric monoidal
$X$
from the symmetric monoidal
![]() $\infty$
-category
$\infty$
-category
 $\mathsf{Perf}(X)_{\otimes }$
. This result extends work by Lurie [Reference LurieLur11], and the classical Tannakian philosophy in general.
$\mathsf{Perf}(X)_{\otimes }$
. This result extends work by Lurie [Reference LurieLur11], and the classical Tannakian philosophy in general.
Corollary 3.32. The functor
 $\mathbb{A}^{\bullet }:(\mathsf{Sch}^{\mathsf{N}})^{\mathsf{op}}\rightarrow \mathsf{Rng}^{\unicode[STIX]{x1D6E5}}$
, sending a Noetherian scheme
$\mathbb{A}^{\bullet }:(\mathsf{Sch}^{\mathsf{N}})^{\mathsf{op}}\rightarrow \mathsf{Rng}^{\unicode[STIX]{x1D6E5}}$
, sending a Noetherian scheme
![]() $X$
to
$X$
to
![]() $\mathbb{A}_{X}^{\bullet }$
, is faithful.
$\mathbb{A}_{X}^{\bullet }$
, is faithful.
Proof. We denote by
![]() $\mathsf{st}_{\otimes }$
the
$\mathsf{st}_{\otimes }$
the
![]() $\infty$
-category of small symmetric monoidal
$\infty$
-category of small symmetric monoidal
![]() $\infty$
-categories. It is shown by Bhatt’s Theorem 3.30(a) that there is a fully faithful functor
$\infty$
-categories. It is shown by Bhatt’s Theorem 3.30(a) that there is a fully faithful functor
 $(\mathsf{Sch}^{\mathsf{qcqs}})^{\mathsf{op}}\rightarrow \mathsf{st}_{\otimes }$
. As our construction has shown, the restriction of this functor to Noetherian schemes, factors through
$(\mathsf{Sch}^{\mathsf{qcqs}})^{\mathsf{op}}\rightarrow \mathsf{st}_{\otimes }$
. As our construction has shown, the restriction of this functor to Noetherian schemes, factors through
 $(\mathsf{Sch}^{\mathsf{N}})^{\mathsf{op}}\rightarrow \mathsf{Rng}^{\unicode[STIX]{x1D6E5}}\rightarrow \mathsf{st}_{\otimes }$
the category of co-simplicial rings. This shows that the functor
$(\mathsf{Sch}^{\mathsf{N}})^{\mathsf{op}}\rightarrow \mathsf{Rng}^{\unicode[STIX]{x1D6E5}}\rightarrow \mathsf{st}_{\otimes }$
the category of co-simplicial rings. This shows that the functor
 $(\mathsf{Sch}^{\mathsf{N}})^{\mathsf{op}}\rightarrow \mathsf{Rng}^{\unicode[STIX]{x1D6E5}}$
is faithful.◻
$(\mathsf{Sch}^{\mathsf{N}})^{\mathsf{op}}\rightarrow \mathsf{Rng}^{\unicode[STIX]{x1D6E5}}$
is faithful.◻
Since the category of quasi-compact and quasi-separated schemes is classical, that is a 1-category, the colimit
 $|\operatorname{Spec}\,\mathbb{A}_{X}^{\bullet }|$
can actually be identified with a co-equaliser.
$|\operatorname{Spec}\,\mathbb{A}_{X}^{\bullet }|$
can actually be identified with a co-equaliser.
Corollary 3.33. For any Noetherian scheme
![]() $X$
we have a canonical equivalence
$X$
we have a canonical equivalence
 $$\begin{eqnarray}\mathsf{colim}[\operatorname{Spec}\mathbb{A}_{X}^{1}\rightrightarrows \operatorname{Spec}\mathbb{A}_{X}^{0}]\simeq X,\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{colim}[\operatorname{Spec}\mathbb{A}_{X}^{1}\rightrightarrows \operatorname{Spec}\mathbb{A}_{X}^{0}]\simeq X,\end{eqnarray}$$
where the co-equaliser is taken in the category of quasi-compact and quasi-separated schemes.
The formalism of derived categories also leads to a rich theory in the case of stacks. Before commenting on this, we continue Remark 3.4.
Remark 3.34. For an algebraic stack
![]() ${\mathcal{Y}}$
one defines
${\mathcal{Y}}$
one defines
![]() $\mathsf{QC}({\mathcal{Y}})$
to be the limit of stable
$\mathsf{QC}({\mathcal{Y}})$
to be the limit of stable
![]() $\infty$
-categories
$\infty$
-categories
 $$\begin{eqnarray}\mathsf{QC}({\mathcal{Y}})=\underset{\operatorname{Spec}R\rightarrow {\mathcal{Y}}}{\mathsf{lim}}\mathsf{QC}(R).\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{QC}({\mathcal{Y}})=\underset{\operatorname{Spec}R\rightarrow {\mathcal{Y}}}{\mathsf{lim}}\mathsf{QC}(R).\end{eqnarray}$$
The recent paper [Reference Bhatt and Halpern-LeistnerBHL15] by Bhatt and Halpern-Leistner extends the aforementioned Tannakian reconstruction result to (spectral) stacks
![]() ${\mathcal{Y}}$
which have property that the derived
${\mathcal{Y}}$
which have property that the derived
![]() $\infty$
-category
$\infty$
-category
![]() $\mathsf{QC}({\mathcal{Y}})$
is compactly generated. This condition can be restrictive in positive characteristic. We refer the reader to Hall and Rydh’s article [Reference Hall and RydhHR15], containing many examples of stacks which do not have this compact generation property.
$\mathsf{QC}({\mathcal{Y}})$
is compactly generated. This condition can be restrictive in positive characteristic. We refer the reader to Hall and Rydh’s article [Reference Hall and RydhHR15], containing many examples of stacks which do not have this compact generation property.
However, it is no longer sufficient to consider only perfect complexes, additionally the notion of connectivity becomes relevant. A complex is said to be connective if it is supported in non-positive degrees.
Corollary 3.35. If
![]() ${\mathcal{Y}}$
is a spectral stack with quasi-affine diagonal, such that the derived category
${\mathcal{Y}}$
is a spectral stack with quasi-affine diagonal, such that the derived category
![]() $\mathsf{QC}({\mathcal{Y}})$
is compactly generated, and
$\mathsf{QC}({\mathcal{Y}})$
is compactly generated, and
![]() $X$
is a Noetherian scheme, then we have
$X$
is a Noetherian scheme, then we have
 ${\mathcal{Y}}(X)\simeq |{\mathcal{Y}}(\mathbb{A}_{X}^{\bullet })|$
.
${\mathcal{Y}}(X)\simeq |{\mathcal{Y}}(\mathbb{A}_{X}^{\bullet })|$
.
Proof. Theorem 3.31 implies that we have an augmentation
 $\operatorname{Spec}\mathbb{A}_{X}^{\bullet }\rightarrow X$
. This induces a canonical augmentation
$\operatorname{Spec}\mathbb{A}_{X}^{\bullet }\rightarrow X$
. This induces a canonical augmentation
 $\mathsf{Map}(X,{\mathcal{Y}})\rightarrow \mathsf{Map}(\operatorname{Spec}\mathbb{A}_{X}^{\bullet },{\mathcal{Y}})$
. To show that it is an equivalence of
$\mathsf{Map}(X,{\mathcal{Y}})\rightarrow \mathsf{Map}(\operatorname{Spec}\mathbb{A}_{X}^{\bullet },{\mathcal{Y}})$
. To show that it is an equivalence of
![]() $\infty$
-groupoids, we use that by [Reference Bhatt and Halpern-LeistnerBHL15, Theorem 4.1] we have fully faithful embedding of
$\infty$
-groupoids, we use that by [Reference Bhatt and Halpern-LeistnerBHL15, Theorem 4.1] we have fully faithful embedding of
![]() $\infty$
-groupoids
$\infty$
-groupoids
 $$\begin{eqnarray}\mathsf{Map}(S,{\mathcal{Y}}){\hookrightarrow}\mathsf{Fun}_{\otimes }^{L}(\mathsf{QC}({\mathcal{Y}}),\mathsf{QC}(S)),\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Map}(S,{\mathcal{Y}}){\hookrightarrow}\mathsf{Fun}_{\otimes }^{L}(\mathsf{QC}({\mathcal{Y}}),\mathsf{QC}(S)),\end{eqnarray}$$
for any scheme
![]() $S$
, where the right-hand side denotes symmetric monoidal functors which commute with colimits. The essential image of this embedding is given by functors which preserve connective objects.
$S$
, where the right-hand side denotes symmetric monoidal functors which commute with colimits. The essential image of this embedding is given by functors which preserve connective objects.
Since
![]() ${\mathcal{Y}}$
is compactly generated, that is
${\mathcal{Y}}$
is compactly generated, that is
 $\mathsf{QC}({\mathcal{Y}})\simeq \mathsf{Ind}\mathsf{QC}({\mathcal{Y}})^{c}$
, we have
$\mathsf{QC}({\mathcal{Y}})\simeq \mathsf{Ind}\mathsf{QC}({\mathcal{Y}})^{c}$
, we have
 $$\begin{eqnarray}\mathsf{Fun}_{\otimes }^{L}(\mathsf{QC}({\mathcal{Y}}),\mathsf{QC}(X))\simeq \mathsf{Fun}_{\otimes }(\mathsf{QC}({\mathcal{Y}})^{c},\mathsf{Perf}(X)).\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Fun}_{\otimes }^{L}(\mathsf{QC}({\mathcal{Y}}),\mathsf{QC}(X))\simeq \mathsf{Fun}_{\otimes }(\mathsf{QC}({\mathcal{Y}})^{c},\mathsf{Perf}(X)).\end{eqnarray}$$
This yields the following commutative diagram.

Since the lower horizontal arrow is an equivalence, and the right-hand vertical arrow is fully faithful, we see that the top horizontal functor
 $\mathsf{Map}(X,{\mathcal{Y}})\rightarrow |\mathsf{Map}(\operatorname{Spec}\mathbb{A}_{X}^{\bullet },{\mathcal{Y}})|$
is fully faithful. It remains to show that it is essentially surjective.
$\mathsf{Map}(X,{\mathcal{Y}})\rightarrow |\mathsf{Map}(\operatorname{Spec}\mathbb{A}_{X}^{\bullet },{\mathcal{Y}})|$
is fully faithful. It remains to show that it is essentially surjective.
Let
 $F^{\bullet }:\mathsf{QC}({\mathcal{Y}})^{c}\rightarrow \mathsf{Perf}(\mathbb{A}_{X}^{\bullet })$
be a cartesian section, corresponding to an object in
$F^{\bullet }:\mathsf{QC}({\mathcal{Y}})^{c}\rightarrow \mathsf{Perf}(\mathbb{A}_{X}^{\bullet })$
be a cartesian section, corresponding to an object in
 $$\begin{eqnarray}|\mathsf{Map}(\operatorname{Spec}\mathbb{A}_{X}^{\bullet },{\mathcal{Y}})|{\hookrightarrow}|\mathsf{Fun}_{\otimes }(\mathsf{QC}({\mathcal{Y}})^{c},\mathsf{Perf}(\mathbb{A}_{X}^{\bullet }))|\simeq \mathsf{Fun}_{\otimes }(\mathsf{QC}({\mathcal{Y}})^{c},\mathsf{Perf}(X)).\end{eqnarray}$$
$$\begin{eqnarray}|\mathsf{Map}(\operatorname{Spec}\mathbb{A}_{X}^{\bullet },{\mathcal{Y}})|{\hookrightarrow}|\mathsf{Fun}_{\otimes }(\mathsf{QC}({\mathcal{Y}})^{c},\mathsf{Perf}(\mathbb{A}_{X}^{\bullet }))|\simeq \mathsf{Fun}_{\otimes }(\mathsf{QC}({\mathcal{Y}})^{c},\mathsf{Perf}(X)).\end{eqnarray}$$
By the stated equivalence this amounts to a symmetric monoidal functor
 $F:\mathsf{QC}({\mathcal{Y}})^{c}\rightarrow \mathsf{Perf}(X)$
. To show that it comes from a morphism
$F:\mathsf{QC}({\mathcal{Y}})^{c}\rightarrow \mathsf{Perf}(X)$
. To show that it comes from a morphism
 $X\rightarrow {\mathcal{Y}}$
it suffices to show by [Reference Bhatt and Halpern-LeistnerBHL15, Theorem 4.1] that the induced symmetric monoidal functor
$X\rightarrow {\mathcal{Y}}$
it suffices to show by [Reference Bhatt and Halpern-LeistnerBHL15, Theorem 4.1] that the induced symmetric monoidal functor
 $F:\mathsf{QC}({\mathcal{Y}})\rightarrow \mathsf{QC}(X)$
preserves connective objects. By Lemma 3.23 a complex
$F:\mathsf{QC}({\mathcal{Y}})\rightarrow \mathsf{QC}(X)$
preserves connective objects. By Lemma 3.23 a complex
![]() $\mathsf{M}^{\bullet }$
of quasi-coherent sheaves is connective if and only if
$\mathsf{M}^{\bullet }$
of quasi-coherent sheaves is connective if and only if
 $\mathsf{M}^{\bullet }\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0}$
is connective (see the first paragraph of the proof of Corollary 3.38 for a similar application of Lemma 3.23). Since the functor
$\mathsf{M}^{\bullet }\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0}$
is connective (see the first paragraph of the proof of Corollary 3.38 for a similar application of Lemma 3.23). Since the functor
![]() $F^{0}$
preserves connective objects by assumption, this shows that so does
$F^{0}$
preserves connective objects by assumption, this shows that so does
![]() $F$
, and hence it belongs to the image of
$F$
, and hence it belongs to the image of
 $\mathsf{Map}(X,{\mathcal{Y}})$
.◻
$\mathsf{Map}(X,{\mathcal{Y}})$
.◻
In positive characteristic, stacks of interest rarely satisfy the condition of
![]() $\mathsf{QC}({\mathcal{Y}})$
being compactly generated. For instance, it may fail for
$\mathsf{QC}({\mathcal{Y}})$
being compactly generated. For instance, it may fail for
![]() $BG$
, where
$BG$
, where
![]() $G$
is a reductive algebraic group. Nonetheless, as we recalled in Theorem 3.30, Bhatt and Halpern-Leistner [Reference Bhatt and Halpern-LeistnerBHL15] also treat the more general case of Noetherian spectral stacks, without the restrictive assumption of compact generation. We will investigate the consequences of their result and adelic descent theory in § 3.2.3. This requires an analysis of pseudo-coherent complexes.
$G$
is a reductive algebraic group. Nonetheless, as we recalled in Theorem 3.30, Bhatt and Halpern-Leistner [Reference Bhatt and Halpern-LeistnerBHL15] also treat the more general case of Noetherian spectral stacks, without the restrictive assumption of compact generation. We will investigate the consequences of their result and adelic descent theory in § 3.2.3. This requires an analysis of pseudo-coherent complexes.
3.2.2 Pseudo-coherence
In this subsection we study the behaviour of pseudo-coherence, also known as almost perfect complexes, with respect to the equivalence
 $\mathsf{QC}(X)\simeq |\mathsf{QC}(\mathbb{A}_{X}^{\bullet })|$
.
$\mathsf{QC}(X)\simeq |\mathsf{QC}(\mathbb{A}_{X}^{\bullet })|$
.
Lemma 3.36. The functor
 $\mathsf{A}_{X}^{0}(-):\mathsf{QCoh}(X)\rightarrow \mathsf{Mod}({\mathcal{O}}_{X})$
is conservative.
$\mathsf{A}_{X}^{0}(-):\mathsf{QCoh}(X)\rightarrow \mathsf{Mod}({\mathcal{O}}_{X})$
is conservative.
Proof. Assume that
 $M\in \mathsf{QCoh}(X)$
is a quasi-coherent sheaf on
$M\in \mathsf{QCoh}(X)$
is a quasi-coherent sheaf on
![]() $X$
, such that
$X$
, such that
 $\mathsf{A}_{X}^{0}(M)=0$
. We have
$\mathsf{A}_{X}^{0}(M)=0$
. We have
 $\unicode[STIX]{x1D6E4}(U,M)=\mathsf{lim}_{\unicode[STIX]{x1D6E5}}\unicode[STIX]{x1D6E4}(U,\mathsf{A}_{X}^{k}(M))$
, where the limit is taken in the category of abelian groups. This limit agrees with the equaliser of
$\unicode[STIX]{x1D6E4}(U,M)=\mathsf{lim}_{\unicode[STIX]{x1D6E5}}\unicode[STIX]{x1D6E4}(U,\mathsf{A}_{X}^{k}(M))$
, where the limit is taken in the category of abelian groups. This limit agrees with the equaliser of
 $[\unicode[STIX]{x1D6E4}(U,\mathsf{A}_{X}^{0}(M))\rightrightarrows \unicode[STIX]{x1D6E4}(U,\mathsf{A}_{X}^{1}(M))]$
, and therefore we see that
$[\unicode[STIX]{x1D6E4}(U,\mathsf{A}_{X}^{0}(M))\rightrightarrows \unicode[STIX]{x1D6E4}(U,\mathsf{A}_{X}^{1}(M))]$
, and therefore we see that
 $\unicode[STIX]{x1D6E4}(U,M)=0$
for all open subsets
$\unicode[STIX]{x1D6E4}(U,M)=0$
for all open subsets
![]() $U$
. This implies
$U$
. This implies
![]() $M=0$
.◻
$M=0$
.◻
Corollary 3.37. If
 $M\in \mathsf{QCoh}(X)$
is a quasi-coherent sheaf, such that
$M\in \mathsf{QCoh}(X)$
is a quasi-coherent sheaf, such that
![]() $\mathsf{A}_{X}^{0}(M)$
is locally finitely generated, then
$\mathsf{A}_{X}^{0}(M)$
is locally finitely generated, then
![]() $M$
is locally finitely generated.
$M$
is locally finitely generated.
Proof. Assume that
![]() $X$
is not locally finitely generated. Then, after replacing
$X$
is not locally finitely generated. Then, after replacing
![]() $X$
by a suitable affine open subset
$X$
by a suitable affine open subset
![]() $U$
, we may construct a surjection
$U$
, we may construct a surjection
 ${\mathcal{O}}_{U}^{\oplus I}{\twoheadrightarrow}M$
, with
${\mathcal{O}}_{U}^{\oplus I}{\twoheadrightarrow}M$
, with
![]() $I$
an infinite set, such that for every finite subset
$I$
an infinite set, such that for every finite subset
![]() $J\subset I$
, the restriction
$J\subset I$
, the restriction
 ${\mathcal{O}}_{U}^{\oplus J}\rightarrow M$
is not surjective. We denote the cokernel of this map by
${\mathcal{O}}_{U}^{\oplus J}\rightarrow M$
is not surjective. We denote the cokernel of this map by
![]() $C_{J}$
.
$C_{J}$
.
However, we know that
![]() $\mathsf{A}_{U}^{0}(M)$
is finitely generated (by Lemma 2.2 a locally finitely generated
$\mathsf{A}_{U}^{0}(M)$
is finitely generated (by Lemma 2.2 a locally finitely generated
![]() $\mathsf{A}_{U}$
-module is globally finitely generated). Hence, there must exist a finite subset
$\mathsf{A}_{U}$
-module is globally finitely generated). Hence, there must exist a finite subset
![]() $J\subset I$
, such that
$J\subset I$
, such that
 $\mathsf{A}_{U}^{0}({\mathcal{O}}_{U})^{\oplus J}{\twoheadrightarrow}\mathsf{A}_{U}^{0}(M)$
is a surjection. Therefore, by the exactness of
$\mathsf{A}_{U}^{0}({\mathcal{O}}_{U})^{\oplus J}{\twoheadrightarrow}\mathsf{A}_{U}^{0}(M)$
is a surjection. Therefore, by the exactness of
![]() $\mathsf{A}_{U}^{0}$
, we obtain
$\mathsf{A}_{U}^{0}$
, we obtain
 $\mathsf{A}_{U}^{0}(C_{J})=0$
. However, by Lemma 3.36, we see that
$\mathsf{A}_{U}^{0}(C_{J})=0$
. However, by Lemma 3.36, we see that
![]() $C_{J}=0$
, and therefore the map
$C_{J}=0$
, and therefore the map
 ${\mathcal{O}}_{X}^{\oplus J}{\twoheadrightarrow}M$
is a surjection as well. This contradicts our assumption.◻
${\mathcal{O}}_{X}^{\oplus J}{\twoheadrightarrow}M$
is a surjection as well. This contradicts our assumption.◻
Corollary 3.38. Let
 $M\in \mathsf{QC}(X)$
be such that
$M\in \mathsf{QC}(X)$
be such that
 $M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0}$
is pseudo-coherent, then
$M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0}$
is pseudo-coherent, then
![]() $M$
is pseudo-coherent.
$M$
is pseudo-coherent.
Proof. Since
![]() $X$
is Noetherian, we only have to show that
$X$
is Noetherian, we only have to show that
 ${\mathcal{H}}^{i}(M)=0$
for
${\mathcal{H}}^{i}(M)=0$
for
![]() $i\gg 0$
, and that every
$i\gg 0$
, and that every
![]() ${\mathcal{H}}^{i}(M)$
is locally finitely generated (see [Sta, Tag 066E]). The first assertion follows directly from Lemmas 3.23 and 3.36. Indeed, we know that
${\mathcal{H}}^{i}(M)$
is locally finitely generated (see [Sta, Tag 066E]). The first assertion follows directly from Lemmas 3.23 and 3.36. Indeed, we know that
 ${\mathcal{H}}^{i}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0})\simeq \mathsf{A}_{X}^{0}({\mathcal{H}}^{i}(M))$
, and that the functor
${\mathcal{H}}^{i}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0})\simeq \mathsf{A}_{X}^{0}({\mathcal{H}}^{i}(M))$
, and that the functor
![]() $\mathsf{A}_{X}^{0}(-)$
is conservative. Therefore, we see that vanishing of
$\mathsf{A}_{X}^{0}(-)$
is conservative. Therefore, we see that vanishing of
 ${\mathcal{H}}^{i}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0})$
in high degrees must imply the same statement for
${\mathcal{H}}^{i}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0})$
in high degrees must imply the same statement for
![]() $M$
.
$M$
.
To show that all cohomology sheaves
![]() ${\mathcal{H}}^{i}(M)$
are locally finitely generated, we may restrict
${\mathcal{H}}^{i}(M)$
are locally finitely generated, we may restrict
![]() $X$
to an affine open subscheme
$X$
to an affine open subscheme
![]() $U\subset X$
. We may assume that
$U\subset X$
. We may assume that
 $M|_{U}\otimes _{{\mathcal{O}}_{U}}\mathsf{A}_{U}^{0}$
is a bounded above complex of finitely generated free
$M|_{U}\otimes _{{\mathcal{O}}_{U}}\mathsf{A}_{U}^{0}$
is a bounded above complex of finitely generated free
![]() $\mathsf{A}_{U}^{0}$
-modules. Therefore, there exists a degree
$\mathsf{A}_{U}^{0}$
-modules. Therefore, there exists a degree
![]() $i$
, such that
$i$
, such that
 ${\mathcal{H}}^{j}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0})=0$
for all
${\mathcal{H}}^{j}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0})=0$
for all
 $j\geqslant i+1$
. In particular, we see that
$j\geqslant i+1$
. In particular, we see that
 ${\mathcal{H}}^{i}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{U}^{i})$
is finitely generated. Since we have that
${\mathcal{H}}^{i}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{U}^{i})$
is finitely generated. Since we have that
 ${\mathcal{H}}^{i}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{U}^{0})\simeq \mathsf{A}_{U}^{0}({\mathcal{H}}^{i}(M))$
, we see from Corollary 3.37 that
${\mathcal{H}}^{i}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{U}^{0})\simeq \mathsf{A}_{U}^{0}({\mathcal{H}}^{i}(M))$
, we see from Corollary 3.37 that
![]() ${\mathcal{H}}^{i}(M)$
is finitely generated.
${\mathcal{H}}^{i}(M)$
is finitely generated.
Consider the distinguished triangle
 $\unicode[STIX]{x1D70F}_{{\leqslant}i-1}M|_{U}\rightarrow M|_{U}\rightarrow {\mathcal{H}}^{i}(M)[-i]|_{U}$
. Since
$\unicode[STIX]{x1D70F}_{{\leqslant}i-1}M|_{U}\rightarrow M|_{U}\rightarrow {\mathcal{H}}^{i}(M)[-i]|_{U}$
. Since
![]() $U$
is Noetherian, the finitely generated module
$U$
is Noetherian, the finitely generated module
![]() ${\mathcal{H}}^{i}$
is pseudo-coherent, and by applying the exact functor
${\mathcal{H}}^{i}$
is pseudo-coherent, and by applying the exact functor
 $-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0}$
we obtain that
$-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0}$
we obtain that
 $\unicode[STIX]{x1D70F}_{{\leqslant}i-1}M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0}$
is also pseudo-coherent. Hence, we conclude that also
$\unicode[STIX]{x1D70F}_{{\leqslant}i-1}M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{0}$
is also pseudo-coherent. Hence, we conclude that also
 ${\mathcal{H}}^{i-1}(\unicode[STIX]{x1D70F}_{{\leqslant}i-1}M)|_{U}={\mathcal{H}}^{i-1}(M)|_{U}$
is finitely generated. Iterating this argument, we see that all cohomology sheaves are locally finitely generated.◻
${\mathcal{H}}^{i-1}(\unicode[STIX]{x1D70F}_{{\leqslant}i-1}M)|_{U}={\mathcal{H}}^{i-1}(M)|_{U}$
is finitely generated. Iterating this argument, we see that all cohomology sheaves are locally finitely generated.◻
We remind the reader that the subscript
![]() $\otimes$
in
$\otimes$
in
![]() $\mathsf{C}_{\otimes }$
refers to the pair given by an
$\mathsf{C}_{\otimes }$
refers to the pair given by an
![]() $\infty$
-category
$\infty$
-category
![]() $\mathsf{C}$
and a symmetric monoidal structure on
$\mathsf{C}$
and a symmetric monoidal structure on
![]() $\mathsf{C}$
.
$\mathsf{C}$
.
Corollary 3.39. We have an equivalence
 $\mathsf{APerf}(X)\simeq |\mathsf{APerf}(\mathbb{A}_{X}^{\bullet })|$
for pseudo-coherent complexes. Similarly, we have an equivalence of symmetric monoidal
$\mathsf{APerf}(X)\simeq |\mathsf{APerf}(\mathbb{A}_{X}^{\bullet })|$
for pseudo-coherent complexes. Similarly, we have an equivalence of symmetric monoidal
![]() $\infty$
-categories
$\infty$
-categories
 $\mathsf{APerf}_{\mathsf{cn}}(X)_{\otimes }\simeq |\mathsf{APerf}_{\mathsf{cn}}(\mathbb{A}_{X}^{\bullet })_{\otimes }|$
, of almost perfect (that is, pseudo-coherent) and connective complexes.
$\mathsf{APerf}_{\mathsf{cn}}(X)_{\otimes }\simeq |\mathsf{APerf}_{\mathsf{cn}}(\mathbb{A}_{X}^{\bullet })_{\otimes }|$
, of almost perfect (that is, pseudo-coherent) and connective complexes.
Proof. We have seen that
 $|\operatorname{Spec}\,\mathbb{A}_{X}^{\bullet }|\rightarrow X$
is an equivalence in the category
$|\operatorname{Spec}\,\mathbb{A}_{X}^{\bullet }|\rightarrow X$
is an equivalence in the category
![]() $\mathsf{Sch}^{\mathsf{qcqs}}$
of quasi-compact and quasi-separated schemes. In particular, we have morphisms of schemes
$\mathsf{Sch}^{\mathsf{qcqs}}$
of quasi-compact and quasi-separated schemes. In particular, we have morphisms of schemes
 $\operatorname{Spec}\mathbb{A}_{X}^{\bullet }\rightarrow X$
, which induce a functor
$\operatorname{Spec}\mathbb{A}_{X}^{\bullet }\rightarrow X$
, which induce a functor
 $\mathsf{APerf}(X)\rightarrow \mathsf{APerf}(\mathbb{A}_{X}^{\bullet })$
, preserving connective objects, and compatible with the equivalence
$\mathsf{APerf}(X)\rightarrow \mathsf{APerf}(\mathbb{A}_{X}^{\bullet })$
, preserving connective objects, and compatible with the equivalence
 $\mathsf{Perf}(X)\simeq |\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })|$
.
$\mathsf{Perf}(X)\simeq |\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })|$
.
The adelic realisation functor
 $-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }:\mathsf{QC}(X)\rightarrow |\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
preserves almost perfect objects and so does the localisation functor
$-\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet }:\mathsf{QC}(X)\rightarrow |\mathsf{QC}(\mathsf{A}_{X}^{\bullet })|$
preserves almost perfect objects and so does the localisation functor
 $\mathsf{Loc}:\mathsf{APerf}(\mathbb{A}_{X}^{\bullet })\rightarrow \mathsf{APerf}(\mathsf{A}_{X}^{\bullet })$
, since it is defined as the tensor product
$\mathsf{Loc}:\mathsf{APerf}(\mathbb{A}_{X}^{\bullet })\rightarrow \mathsf{APerf}(\mathsf{A}_{X}^{\bullet })$
, since it is defined as the tensor product
 $-\otimes _{\mathbb{A}_{X}^{\bullet }}\mathsf{A}_{X}^{\bullet }$
.
$-\otimes _{\mathbb{A}_{X}^{\bullet }}\mathsf{A}_{X}^{\bullet }$
.
We have seen in Lemma 3.23 that for every complex
 $M\in \mathsf{QC}(X)$
we have
$M\in \mathsf{QC}(X)$
we have
 $\mathsf{A}_{X}^{\bullet }({\mathcal{H}}^{i}(M))={\mathcal{H}}^{i}(\mathsf{A}_{X}^{\bullet }\otimes _{{\mathcal{O}}_{X}}M)$
. Together with Theorem 1.16 this implies
$\mathsf{A}_{X}^{\bullet }({\mathcal{H}}^{i}(M))={\mathcal{H}}^{i}(\mathsf{A}_{X}^{\bullet }\otimes _{{\mathcal{O}}_{X}}M)$
. Together with Theorem 1.16 this implies
 ${\mathcal{H}}^{i}(M)=|{\mathcal{H}}^{i}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet })|$
. We see that
${\mathcal{H}}^{i}(M)=|{\mathcal{H}}^{i}(M\otimes _{{\mathcal{O}}_{X}}\mathsf{A}_{X}^{\bullet })|$
. We see that
![]() $M$
is connective if and only if
$M$
is connective if and only if
 $\mathsf{A}_{X}^{\bullet }\otimes _{{\mathcal{O}}_{X}}M$
is. We have seen in Corollary 3.38 that
$\mathsf{A}_{X}^{\bullet }\otimes _{{\mathcal{O}}_{X}}M$
is. We have seen in Corollary 3.38 that
 $M\in \mathsf{QC}(X)$
is pseudo-coherent, if and only if
$M\in \mathsf{QC}(X)$
is pseudo-coherent, if and only if
 $\mathsf{A}_{X}^{\bullet }\otimes _{{\mathcal{O}}_{X}}M$
is pseudo-coherent. This shows that the image of a pseudo-coherent, and connective
$\mathsf{A}_{X}^{\bullet }\otimes _{{\mathcal{O}}_{X}}M$
is pseudo-coherent. This shows that the image of a pseudo-coherent, and connective
 $M\in \mathsf{APerf}_{\mathsf{cn}}(\mathbb{A}_{X}^{\bullet })$
lies inside
$M\in \mathsf{APerf}_{\mathsf{cn}}(\mathbb{A}_{X}^{\bullet })$
lies inside
 $\mathsf{APerf}_{cn}(X)$
.
$\mathsf{APerf}_{cn}(X)$
.
We conclude that both directions of the equivalence
 $\mathsf{Ind}\mathsf{Perf}(X)\simeq \mathsf{Ind}|\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })|$
respect almost perfect and connective objects. Hence, we obtain the equivalences
$\mathsf{Ind}\mathsf{Perf}(X)\simeq \mathsf{Ind}|\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })|$
respect almost perfect and connective objects. Hence, we obtain the equivalences
 $\mathsf{APerf}(X)\simeq |\mathsf{APerf}(\mathbb{A}_{X}^{\bullet })|$
and
$\mathsf{APerf}(X)\simeq |\mathsf{APerf}(\mathbb{A}_{X}^{\bullet })|$
and
 $\mathsf{APerf}_{\mathsf{cn}}(X)\simeq |\mathsf{APerf}_{\mathsf{cn}}(\mathbb{A}_{X}^{\bullet })|$
.◻
$\mathsf{APerf}_{\mathsf{cn}}(X)\simeq |\mathsf{APerf}_{\mathsf{cn}}(\mathbb{A}_{X}^{\bullet })|$
.◻
3.2.3 Adèles and maps to Noetherian stacks
We will see that
![]() $X$
remains the colimit of the diagram
$X$
remains the colimit of the diagram
 $\operatorname{Spec}\mathbb{A}_{X}^{\bullet }$
in the
$\operatorname{Spec}\mathbb{A}_{X}^{\bullet }$
in the
![]() $\infty$
-category of Noetherian stacks.
$\infty$
-category of Noetherian stacks.
Theorem 3.40. Let
![]() $X$
be a Noetherian scheme, and
$X$
be a Noetherian scheme, and
![]() ${\mathcal{Y}}$
a spectral Noetherian stack with quasi-affine diagonal. We then have a canonical equivalence
${\mathcal{Y}}$
a spectral Noetherian stack with quasi-affine diagonal. We then have a canonical equivalence
 ${\mathcal{Y}}(X)\simeq {\mathcal{Y}}(\operatorname{Spec}\mathbb{A}_{X}^{\bullet })$
, that is,
${\mathcal{Y}}(X)\simeq {\mathcal{Y}}(\operatorname{Spec}\mathbb{A}_{X}^{\bullet })$
, that is,
![]() $X$
the equivalent to the colimit
$X$
the equivalent to the colimit
 $|\operatorname{Spec}\,\mathbb{A}_{X}^{\bullet }|$
in the
$|\operatorname{Spec}\,\mathbb{A}_{X}^{\bullet }|$
in the
![]() $\infty$
-category of spectral Noetherian stacks with quasi-affine diagonal.
$\infty$
-category of spectral Noetherian stacks with quasi-affine diagonal.
Proof. We have shown in Corollary 3.39 that we have an equivalence
 $\mathsf{APerf}(X)_{\otimes }\simeq |\mathsf{APerf}(\mathbb{A}_{X}^{\bullet })_{\otimes }|$
. By means of [Reference Bhatt and Halpern-LeistnerBHL15, Lemma 3.12 and Theorem 1.4] we see that this equivalence realises
$\mathsf{APerf}(X)_{\otimes }\simeq |\mathsf{APerf}(\mathbb{A}_{X}^{\bullet })_{\otimes }|$
. By means of [Reference Bhatt and Halpern-LeistnerBHL15, Lemma 3.12 and Theorem 1.4] we see that this equivalence realises
![]() $X$
as a colimit of
$X$
as a colimit of
 $\operatorname{Spec}\mathbb{A}_{X}^{\bullet }$
in the category of spectral Noetherian stacks.◻
$\operatorname{Spec}\mathbb{A}_{X}^{\bullet }$
in the category of spectral Noetherian stacks.◻
If
![]() ${\mathcal{Y}}$
is a classical Noetherian stack, that is a groupoid-valued functor
${\mathcal{Y}}$
is a classical Noetherian stack, that is a groupoid-valued functor
 $\operatorname{Aff}^{\mathsf{op}}\rightarrow \mathsf{Grpd}$
, we may take advantage of the fact that
$\operatorname{Aff}^{\mathsf{op}}\rightarrow \mathsf{Grpd}$
, we may take advantage of the fact that
![]() $\mathsf{Grpd}$
form a
$\mathsf{Grpd}$
form a
![]() $2$
-category to simplify the limit
$2$
-category to simplify the limit
 $|{\mathcal{Y}}(\operatorname{Spec}\mathbb{A}_{X}^{\bullet })|$
.
$|{\mathcal{Y}}(\operatorname{Spec}\mathbb{A}_{X}^{\bullet })|$
.
Corollary 3.41. Let
![]() ${\mathcal{Y}}$
be a Noetherian stack with quasi-affine diagonal, taking values in the
${\mathcal{Y}}$
be a Noetherian stack with quasi-affine diagonal, taking values in the
![]() $2$
-category of groupoids. Then, we have an equivalence of groupoids
$2$
-category of groupoids. Then, we have an equivalence of groupoids

where the limit is taken in the
![]() $2$
-category of groupoids.
$2$
-category of groupoids.
3.2.4 The special case of
 $G$
-bundles
$G$
-bundles
A special case of Corollary 3.41 of particular interest to us is the following generalisation of Weil’s theorem to arbitrary Noetherian schemes.
Corollary 3.42. Let
![]() $G$
be an affine Noetherian group scheme, and
$G$
be an affine Noetherian group scheme, and
![]() $X$
a Noetherian scheme. Then we have a canonical equivalence
$X$
a Noetherian scheme. Then we have a canonical equivalence

For
 $G=\operatorname{GL}_{n}$
and a scheme
$G=\operatorname{GL}_{n}$
and a scheme
![]() $U$
,
$U$
,
 $B\operatorname{GL}_{n}(U)$
is equivalent to the groupoid
$B\operatorname{GL}_{n}(U)$
is equivalent to the groupoid
 $\operatorname{Vect}_{n}(U)$
of rank
$\operatorname{Vect}_{n}(U)$
of rank
![]() $n$
vector bundles on
$n$
vector bundles on
![]() $U$
. We write
$U$
. We write
 $\operatorname{Vect}_{n}^{f}(U)$
for full subgroupoid, consisting only of trivial rank
$\operatorname{Vect}_{n}^{f}(U)$
for full subgroupoid, consisting only of trivial rank
![]() $n$
bundles.
$n$
bundles.
Let
 $E\in \operatorname{Vect}_{n}(X)$
be a rank
$E\in \operatorname{Vect}_{n}(X)$
be a rank
![]() $n$
vector bundle on
$n$
vector bundle on
![]() $X$
. Since finitely generated projective modules over local rings are free, we may choose a trivialisation
$X$
. Since finitely generated projective modules over local rings are free, we may choose a trivialisation
 $E_{x}\simeq {\mathcal{O}}_{x}^{\oplus n}$
, for every
$E_{x}\simeq {\mathcal{O}}_{x}^{\oplus n}$
, for every
![]() $x\in |X|$
. This implies that
$x\in |X|$
. This implies that
![]() $\mathbb{A}_{X}^{0}(E)$
is a trivial rank
$\mathbb{A}_{X}^{0}(E)$
is a trivial rank
![]() $n$
module over
$n$
module over
![]() $\mathbb{A}_{X}^{0}$
. Hence, we obtain an equivalence
$\mathbb{A}_{X}^{0}$
. Hence, we obtain an equivalence

For
 $E\in \operatorname{Vect}_{n}(X)$
we denote the corresponding objects in
$E\in \operatorname{Vect}_{n}(X)$
we denote the corresponding objects in
 $\operatorname{Vect}_{n}^{f}(\mathbb{A}_{X}^{i})$
by
$\operatorname{Vect}_{n}^{f}(\mathbb{A}_{X}^{i})$
by
![]() $E^{i}$
. The choice of a trivialisation
$E^{i}$
. The choice of a trivialisation
 $E^{0}\simeq (\mathbb{A}_{X}^{0})^{\oplus n}$
induces two trivialisations
$E^{0}\simeq (\mathbb{A}_{X}^{0})^{\oplus n}$
induces two trivialisations
 $\unicode[STIX]{x1D713}_{i}:E^{1}\simeq (\mathbb{A}_{X}^{1})^{\oplus n}$
for
$\unicode[STIX]{x1D713}_{i}:E^{1}\simeq (\mathbb{A}_{X}^{1})^{\oplus n}$
for
![]() $i=0,1$
. The trivialisations are obtained by means of the defining property of a cartesian module. Let
$i=0,1$
. The trivialisations are obtained by means of the defining property of a cartesian module. Let
 $\unicode[STIX]{x2202}_{i}:\{i\}{\hookrightarrow}\{0,1\}=[1]$
in
$\unicode[STIX]{x2202}_{i}:\{i\}{\hookrightarrow}\{0,1\}=[1]$
in
![]() $\unicode[STIX]{x1D6E5}$
. Since
$\unicode[STIX]{x1D6E5}$
. Since
![]() $E^{\bullet }$
is a cartesian
$E^{\bullet }$
is a cartesian
![]() $\mathbb{A}_{X}^{\bullet }$
-module, we have
$\mathbb{A}_{X}^{\bullet }$
-module, we have
 $E^{1}\simeq E^{0}\otimes _{\mathbb{A}_{X}^{0},\unicode[STIX]{x2202}_{i}}\mathbb{A}_{X}^{1}$
. We let
$E^{1}\simeq E^{0}\otimes _{\mathbb{A}_{X}^{0},\unicode[STIX]{x2202}_{i}}\mathbb{A}_{X}^{1}$
. We let
 $\unicode[STIX]{x1D719}\in \operatorname{GL}_{n}(\mathbb{A}_{X}^{1})$
be the linear map
$\unicode[STIX]{x1D719}\in \operatorname{GL}_{n}(\mathbb{A}_{X}^{1})$
be the linear map
 $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D713}_{0}\circ \unicode[STIX]{x1D713}_{1}^{-1}:(\mathbb{A}_{X}^{1})^{\oplus n}\rightarrow (\mathbb{A}_{X}^{1})^{\oplus n}$
.
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D713}_{0}\circ \unicode[STIX]{x1D713}_{1}^{-1}:(\mathbb{A}_{X}^{1})^{\oplus n}\rightarrow (\mathbb{A}_{X}^{1})^{\oplus n}$
.
For
 $0\leqslant i<j\leqslant 2$
, we denote by
$0\leqslant i<j\leqslant 2$
, we denote by
 $\unicode[STIX]{x2202}_{ij}:\{i,j\}{\hookrightarrow}\{0,1,2\}=[2]$
in
$\unicode[STIX]{x2202}_{ij}:\{i,j\}{\hookrightarrow}\{0,1,2\}=[2]$
in
![]() $\unicode[STIX]{x1D6E5}$
. We denote by
$\unicode[STIX]{x1D6E5}$
. We denote by
 $\unicode[STIX]{x1D719}_{ij}=\unicode[STIX]{x1D719}\otimes _{\mathbb{A}_{X}^{1},\unicode[STIX]{x2202}_{ij}}\mathbb{A}_{X}^{2}\in \operatorname{GL}_{n}(\mathbb{A}_{X}^{2})$
. By construction of
$\unicode[STIX]{x1D719}_{ij}=\unicode[STIX]{x1D719}\otimes _{\mathbb{A}_{X}^{1},\unicode[STIX]{x2202}_{ij}}\mathbb{A}_{X}^{2}\in \operatorname{GL}_{n}(\mathbb{A}_{X}^{2})$
. By construction of
![]() $\unicode[STIX]{x1D719}$
the cocycle identity
$\unicode[STIX]{x1D719}$
the cocycle identity
 $\unicode[STIX]{x1D719}_{02}=\unicode[STIX]{x1D719}_{01}\circ \unicode[STIX]{x1D719}_{12}$
is satisfied.
$\unicode[STIX]{x1D719}_{02}=\unicode[STIX]{x1D719}_{01}\circ \unicode[STIX]{x1D719}_{12}$
is satisfied.
Vice versa, every
 $\unicode[STIX]{x1D719}\in \operatorname{GL}_{n}(\mathbb{A}_{X}^{1})$
, satisfying the cocycle identity
$\unicode[STIX]{x1D719}\in \operatorname{GL}_{n}(\mathbb{A}_{X}^{1})$
, satisfying the cocycle identity
 $\unicode[STIX]{x1D719}_{02}=\unicode[STIX]{x1D719}_{01}\circ \unicode[STIX]{x1D719}_{12}$
, corresponds to an object
$\unicode[STIX]{x1D719}_{02}=\unicode[STIX]{x1D719}_{01}\circ \unicode[STIX]{x1D719}_{12}$
, corresponds to an object  plus the choice of a trivialisation
plus the choice of a trivialisation
 $E^{0}\simeq (\mathbb{A}_{X}^{0})^{\oplus n}$
. Summarising we obtain interpretation of Corollary 3.42.
$E^{0}\simeq (\mathbb{A}_{X}^{0})^{\oplus n}$
. Summarising we obtain interpretation of Corollary 3.42.
Corollary 3.43. Let
![]() $X$
be a Noetherian scheme and
$X$
be a Noetherian scheme and
![]() $G$
a special group scheme (that is, every
$G$
a special group scheme (that is, every
![]() $G$
-bundle on a Noetherian scheme is Zariski-locally trivial). We denote by
$G$
-bundle on a Noetherian scheme is Zariski-locally trivial). We denote by
 $G(\mathbb{A}_{X}^{1})^{\text{cocycle}}$
the subset consisting of
$G(\mathbb{A}_{X}^{1})^{\text{cocycle}}$
the subset consisting of
 $\unicode[STIX]{x1D719}\in G(\mathbb{A}_{X}^{1})$
satisfying the cocycle condition
$\unicode[STIX]{x1D719}\in G(\mathbb{A}_{X}^{1})$
satisfying the cocycle condition
 $\unicode[STIX]{x1D719}_{02}=\unicode[STIX]{x1D719}_{01}\circ \unicode[STIX]{x1D719}_{12}$
in
$\unicode[STIX]{x1D719}_{02}=\unicode[STIX]{x1D719}_{01}\circ \unicode[STIX]{x1D719}_{12}$
in
![]() $G(\mathbb{A}_{X}^{2})$
. Then, we have an equivalence of groupoids
$G(\mathbb{A}_{X}^{2})$
. Then, we have an equivalence of groupoids
 $BG(X)\simeq [G(\mathbb{A}_{X}^{1})^{\text{cocycle}}/G(\mathbb{A}_{X}^{0})]$
.
$BG(X)\simeq [G(\mathbb{A}_{X}^{1})^{\text{cocycle}}/G(\mathbb{A}_{X}^{0})]$
.
When
![]() $X$
is a curve, Weil’s formulation
$X$
is a curve, Weil’s formulation
 $BG(X)\simeq [G(F_{X})\setminus G(\mathbb{A}_{X})/G(\mathbb{O}_{X})]$
can be directly deduced from the aforementioned one. Recall that
$BG(X)\simeq [G(F_{X})\setminus G(\mathbb{A}_{X})/G(\mathbb{O}_{X})]$
can be directly deduced from the aforementioned one. Recall that
 $\mathbb{A}_{X}^{1}=F_{X}\times \mathbb{O}_{X}\times \mathbb{A}_{X}$
, and that
$\mathbb{A}_{X}^{1}=F_{X}\times \mathbb{O}_{X}\times \mathbb{A}_{X}$
, and that
 $\mathbb{A}_{X}^{2}=\mathbb{A}_{X}^{1}$
for dimension reasons. Therefore,
$\mathbb{A}_{X}^{2}=\mathbb{A}_{X}^{1}$
for dimension reasons. Therefore,
 $G(\mathbb{A}_{X}^{1})^{\text{cocycle}}=G(\mathbb{A}_{X}^{1})$
, and we obtain the quotient
$G(\mathbb{A}_{X}^{1})^{\text{cocycle}}=G(\mathbb{A}_{X}^{1})$
, and we obtain the quotient
 $$\begin{eqnarray}[G(F_{X})\times G(\mathbb{O}_{X})\times G(\mathbb{A}_{X})/G(F_{X})\times G(\mathbb{O}_{X})]\simeq [G(F_{X})\setminus G(\mathbb{A}_{X})/G(\mathbb{O}_{X})].\end{eqnarray}$$
$$\begin{eqnarray}[G(F_{X})\times G(\mathbb{O}_{X})\times G(\mathbb{A}_{X})/G(F_{X})\times G(\mathbb{O}_{X})]\simeq [G(F_{X})\setminus G(\mathbb{A}_{X})/G(\mathbb{O}_{X})].\end{eqnarray}$$
Remark 3.44. In [Reference HuberHub91, § 5.2] Huber defines rational adèles
![]() $a_{X}^{\bullet }$
. The arguments of this paper also apply to
$a_{X}^{\bullet }$
. The arguments of this paper also apply to
![]() $a_{X}^{\bullet }$
, in fact the proofs can be slightly simplified in this case.
$a_{X}^{\bullet }$
, in fact the proofs can be slightly simplified in this case.
Acknowledgements
The author first conjectured the main theorem during a conversation with Bertrand Toën. I thank him for his interest and encouragement, which subsequently led to the present work. Moreover, I thank Hélène Esnault, Gabriele Vezzosi and Darya Schedrina for their interest and discussions about the paper. I am grateful to Dennis Gaitsgory for alerting me to an erroneous lemma contained in a preliminary version of this paper. I also thank the anonymous referee for a careful reading of the manuscript and for making many valuable suggestions. Through joint work with Oliver Bräunling and Jesse Wolfson I was introduced to the fascinating world of adèles and its curious interplay with algebraic geometry. It is a pleasure to thank them for all the mathematics they taught me. Their influence on my thinking permeates the entire text. I am grateful for EPSRC funding received under P/G06170X/1.
Appendix A Results from
 $\infty$
-category theory
$\infty$
-category theory
An
![]() $\infty$
-category
$\infty$
-category
![]() $\mathsf{C}$
is called small if it is equivalent to an
$\mathsf{C}$
is called small if it is equivalent to an
![]() $\infty$
-category modelled by a quasi-category whose underlying simplicial set is small. If
$\infty$
-category modelled by a quasi-category whose underlying simplicial set is small. If
![]() $\mathsf{C}$
is a classical category, this is tantamount to
$\mathsf{C}$
is a classical category, this is tantamount to
![]() $\mathsf{C}$
being equivalent to a category, for which the class of objects, and morphism sets for every pair of objects, form small sets.
$\mathsf{C}$
being equivalent to a category, for which the class of objects, and morphism sets for every pair of objects, form small sets.
We say that
![]() $\mathsf{C}$
is locally small if for every pair of objects
$\mathsf{C}$
is locally small if for every pair of objects
![]() $X,Y$
, the mapping space
$X,Y$
, the mapping space
 $\mathsf{Map}(X,Y)$
can be modelled by a small Kan complex (see [Reference LurieLur07, Definition 5.4.1.7]). For a classical category
$\mathsf{Map}(X,Y)$
can be modelled by a small Kan complex (see [Reference LurieLur07, Definition 5.4.1.7]). For a classical category
![]() $\mathsf{C}$
this amounts to the condition that
$\mathsf{C}$
this amounts to the condition that
 $\mathsf{Map}(X,Y)$
is a small set.
$\mathsf{Map}(X,Y)$
is a small set.
We will only consider locally small
![]() $\infty$
-categories. Because we are sometimes taking limits of
$\infty$
-categories. Because we are sometimes taking limits of
![]() $\infty$
-categories (over small diagrams), it is important to observe that this operation will preserve local smallness.
$\infty$
-categories (over small diagrams), it is important to observe that this operation will preserve local smallness.
Remark A.1. Let
 $\mathsf{C}_{-}:K\rightarrow \infty \text{-}\mathsf{Cat}$
be a diagram of
$\mathsf{C}_{-}:K\rightarrow \infty \text{-}\mathsf{Cat}$
be a diagram of
![]() $\infty$
-categories, such that
$\infty$
-categories, such that
![]() $K$
is a small simplicial set, and for each
$K$
is a small simplicial set, and for each
![]() $k\in K$
we have that
$k\in K$
we have that
![]() $\mathsf{C}_{k}$
is a locally small
$\mathsf{C}_{k}$
is a locally small
![]() $\infty$
-category. Then, the limit
$\infty$
-category. Then, the limit
 $\mathsf{lim}_{k\in K}\mathsf{C}_{k}$
is also a locally small
$\mathsf{lim}_{k\in K}\mathsf{C}_{k}$
is also a locally small
![]() $\infty$
-category.
$\infty$
-category.
The reader may easily verify this assertion with the help of [Reference LurieLur07, Corollary 3.3.3.2], which identifies the limit
 $\mathsf{C}=\mathsf{lim}_{k\in K}\mathsf{C}_{k}$
with the
$\mathsf{C}=\mathsf{lim}_{k\in K}\mathsf{C}_{k}$
with the
![]() $\infty$
-category of cartesian sections, of a cartesian fibration
$\infty$
-category of cartesian sections, of a cartesian fibration
![]() $\widetilde{\mathsf{C}}\rightarrow K$
, corresponding to the functor
$\widetilde{\mathsf{C}}\rightarrow K$
, corresponding to the functor
![]() $\mathsf{C}_{-}$
. This implies that the mapping spaces in
$\mathsf{C}_{-}$
. This implies that the mapping spaces in
![]() $\mathsf{C}$
are equivalent to the mapping spaces in the
$\mathsf{C}$
are equivalent to the mapping spaces in the
![]() $\infty$
-category of cartesian sections of
$\infty$
-category of cartesian sections of
![]() $\widetilde{\mathsf{C}}\rightarrow K$
. If
$\widetilde{\mathsf{C}}\rightarrow K$
. If
 $X,Y:K\rightarrow \widetilde{\mathsf{C}}$
are two such sections, then we obtain
$X,Y:K\rightarrow \widetilde{\mathsf{C}}$
are two such sections, then we obtain
 $$\begin{eqnarray}\mathsf{Map}(X,Y)\simeq \underset{k\in K}{\mathsf{lim}}\mathsf{Map}(X_{k},Y_{k}).\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Map}(X,Y)\simeq \underset{k\in K}{\mathsf{lim}}\mathsf{Map}(X_{k},Y_{k}).\end{eqnarray}$$
Since small limits of small spaces remain small, we conclude that
![]() $\mathsf{C}$
is locally small. The description of mapping spaces in limits of
$\mathsf{C}$
is locally small. The description of mapping spaces in limits of
![]() $\infty$
-categories will be recorded for future reference.
$\infty$
-categories will be recorded for future reference.
Lemma A.2. Let
 $\mathsf{C}_{-}:K\rightarrow \mathsf{C}$
be a diagram of
$\mathsf{C}_{-}:K\rightarrow \mathsf{C}$
be a diagram of
![]() $\infty$
-categories, parametrised by a small simplicial set
$\infty$
-categories, parametrised by a small simplicial set
![]() $K$
. We denote by
$K$
. We denote by
 $\mathsf{C}=\mathsf{lim}_{k\in K}\mathsf{C}_{k}$
the limit of this diagram. Given objects
$\mathsf{C}=\mathsf{lim}_{k\in K}\mathsf{C}_{k}$
the limit of this diagram. Given objects
 $X,Y\in \mathsf{C}$
, we have a canonical equivalence of spaces
$X,Y\in \mathsf{C}$
, we have a canonical equivalence of spaces
 $\mathsf{Map}(X,Y)\simeq \mathsf{lim}_{k\in K}(X_{k},Y_{k})$
.
$\mathsf{Map}(X,Y)\simeq \mathsf{lim}_{k\in K}(X_{k},Y_{k})$
.
The following result is [Reference LurieLur07, Corollary 5.5.2.9 and Remark 5.5.2.10].
Theorem A.3 (Lurie’s adjoint functor theorem).
Let
 $F:\mathsf{C}\rightarrow \mathsf{D}$
be a functor between stable
$F:\mathsf{C}\rightarrow \mathsf{D}$
be a functor between stable
![]() $\infty$
-categories. If
$\infty$
-categories. If
![]() $\mathsf{C}$
is presentable and
$\mathsf{C}$
is presentable and
![]() $\mathsf{D}$
locally small, then
$\mathsf{D}$
locally small, then
![]() $F$
admits a right adjoint
$F$
admits a right adjoint
 $G:\mathsf{D}\rightarrow \mathsf{C}$
, if and only if
$G:\mathsf{D}\rightarrow \mathsf{C}$
, if and only if
![]() $F$
preserves small colimits.
$F$
preserves small colimits.
We refer the reader to [Reference LurieLur, Proposition 1.4.4.1.] for a proof of the following result.
Proposition A.4. If
![]() $\mathsf{C}$
is a stable
$\mathsf{C}$
is a stable
![]() $\infty$
-category, admitting arbitrary coproducts, then
$\infty$
-category, admitting arbitrary coproducts, then
![]() $\mathsf{C}$
possesses all small colimits. Moreover, let
$\mathsf{C}$
possesses all small colimits. Moreover, let
 $F:\mathsf{C}\rightarrow \mathsf{D}$
be an exact functor between cocomplete stable
$F:\mathsf{C}\rightarrow \mathsf{D}$
be an exact functor between cocomplete stable
![]() $\infty$
-categories, commuting with small coproducts. Then,
$\infty$
-categories, commuting with small coproducts. Then,
![]() $F$
commutes with small colimits.
$F$
commutes with small colimits.
The notion of compact objects in stable
![]() $\infty$
-categories will be essential to us. There are two equivalent characterisations of compactness. We refer the reader to [Reference LurieLur, Proposition 1.4.4.1] for a proof of equivalence.
$\infty$
-categories will be essential to us. There are two equivalent characterisations of compactness. We refer the reader to [Reference LurieLur, Proposition 1.4.4.1] for a proof of equivalence.
Definition A.5. Let
![]() $\mathsf{C}$
be a stable
$\mathsf{C}$
be a stable
![]() $\infty$
-category. An object
$\infty$
-category. An object
![]() $X\in \mathsf{C}$
is called compact, if
$X\in \mathsf{C}$
is called compact, if
 $\mathsf{Hom}(X,-)$
commutes with small coproducts. Equivalently, for
$\mathsf{Hom}(X,-)$
commutes with small coproducts. Equivalently, for
 $(Y_{i})_{i\in I}\in \mathsf{C}$
, a small family of objects in
$(Y_{i})_{i\in I}\in \mathsf{C}$
, a small family of objects in
![]() $\mathsf{C}$
, for every morphism
$\mathsf{C}$
, for every morphism
 $X\rightarrow \bigoplus _{i\in I}Y_{i}$
, there exists a finite subset
$X\rightarrow \bigoplus _{i\in I}Y_{i}$
, there exists a finite subset
![]() $J\subset I$
, such that the map factors through
$J\subset I$
, such that the map factors through
 $\bigoplus _{i\in J}Y_{i}\rightarrow \bigoplus _{i\in I}Y_{i}$
.
$\bigoplus _{i\in J}Y_{i}\rightarrow \bigoplus _{i\in I}Y_{i}$
.
The full subcategory of compact objects of
![]() $\mathsf{C}$
will be denoted by
$\mathsf{C}$
will be denoted by
![]() $\mathsf{C}^{\text{c}}$
. We say that
$\mathsf{C}^{\text{c}}$
. We say that
![]() $\mathsf{C}$
is compactly generated, if
$\mathsf{C}$
is compactly generated, if
 $\mathsf{C}\simeq \mathsf{Ind}\mathsf{C}^{\text{c}}$
.
$\mathsf{C}\simeq \mathsf{Ind}\mathsf{C}^{\text{c}}$
.
Lemma A.6. Let
 $F:\mathsf{C}\rightarrow \mathsf{D}$
be an exact functor between cocomplete stable
$F:\mathsf{C}\rightarrow \mathsf{D}$
be an exact functor between cocomplete stable
![]() $\infty$
-categories, with a right adjoint
$\infty$
-categories, with a right adjoint
![]() $G$
. If
$G$
. If
![]() $\mathsf{C}$
is compactly generated, and
$\mathsf{C}$
is compactly generated, and
![]() $F$
preserves compact objects, then
$F$
preserves compact objects, then
![]() $G$
commutes with small colimits.
$G$
commutes with small colimits.
Proof. By Proposition A.4 it suffices to show that
![]() $G$
commutes with small coproducts. That is, for
$G$
commutes with small coproducts. That is, for
![]() $\{Y_{i}\}_{i\in I}$
, where
$\{Y_{i}\}_{i\in I}$
, where
![]() $I$
is a small set indexing objects in
$I$
is a small set indexing objects in
![]() $\mathsf{D}$
, we have to show that the natural map
$\mathsf{D}$
, we have to show that the natural map
 $\bigoplus _{i\in I}G(Y_{i})\rightarrow G(\bigoplus _{i\in I}Y_{i})$
is an equivalence. Since
$\bigoplus _{i\in I}G(Y_{i})\rightarrow G(\bigoplus _{i\in I}Y_{i})$
is an equivalence. Since
![]() $\mathsf{C}$
is compactly generated, this is equivalent to
$\mathsf{C}$
is compactly generated, this is equivalent to
 $$\begin{eqnarray}\mathsf{Hom}\biggl(X,\bigoplus _{i\in I}G(Y_{i})\biggr)\rightarrow \mathsf{Hom}\biggl(X,G\biggl(\bigoplus _{i\in I}Y_{i}\biggr)\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Hom}\biggl(X,\bigoplus _{i\in I}G(Y_{i})\biggr)\rightarrow \mathsf{Hom}\biggl(X,G\biggl(\bigoplus _{i\in I}Y_{i}\biggr)\biggr)\end{eqnarray}$$
being an equivalence for every compact object
![]() $X\in \mathsf{C}$
. Compactness of
$X\in \mathsf{C}$
. Compactness of
![]() $X$
, and the adjunction between
$X$
, and the adjunction between
![]() $F$
and
$F$
and
![]() $G$
allows us to show instead that the map
$G$
allows us to show instead that the map
 $$\begin{eqnarray}\bigoplus _{i\in I}\mathsf{Hom}(F(X),Y_{i})\rightarrow \bigoplus _{i\in I}\mathsf{Hom}(F(X),Y_{i})\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{i\in I}\mathsf{Hom}(F(X),Y_{i})\rightarrow \bigoplus _{i\in I}\mathsf{Hom}(F(X),Y_{i})\end{eqnarray}$$
is an equivalence. However, this is a morphism equivalent to the identity map. ◻
The following is a well-known criterion for an adjunction to be an equivalence.
Lemma A.7. Let
 $F:\mathsf{C}\rightarrow \mathsf{D}$
be a functor between
$F:\mathsf{C}\rightarrow \mathsf{D}$
be a functor between
![]() $\infty$
-categories with right adjoint
$\infty$
-categories with right adjoint
![]() $G$
. If
$G$
. If
![]() $F$
is fully faithful and
$F$
is fully faithful and
![]() $G$
is conservative, then
$G$
is conservative, then
![]() $F$
and
$F$
and
![]() $G$
are mutually inverse equivalences.
$G$
are mutually inverse equivalences.
Proof. Since
![]() $F$
is fully faithful, the unit
$F$
is fully faithful, the unit
 $\operatorname{id}_{\mathsf{C}}\rightarrow \mathit{GF}$
is an equivalence of functors. It remains to check that the co-unit
$\operatorname{id}_{\mathsf{C}}\rightarrow \mathit{GF}$
is an equivalence of functors. It remains to check that the co-unit
 $\mathit{FG}\rightarrow \operatorname{id}_{\mathsf{D}}$
is an equivalence. By assumption,
$\mathit{FG}\rightarrow \operatorname{id}_{\mathsf{D}}$
is an equivalence. By assumption,
![]() $G$
is conservative, therefore it suffices to prove that
$G$
is conservative, therefore it suffices to prove that
 $\mathit{GFG}\rightarrow G$
is an equivalence of functors. By the standard properties of adjunctions, the composition
$\mathit{GFG}\rightarrow G$
is an equivalence of functors. By the standard properties of adjunctions, the composition
 $$\begin{eqnarray}G\simeq \operatorname{id}_{\mathsf{C}}G\simeq \mathit{GFG}\rightarrow G\operatorname{id}_{\mathsf{D}}\simeq G\end{eqnarray}$$
$$\begin{eqnarray}G\simeq \operatorname{id}_{\mathsf{C}}G\simeq \mathit{GFG}\rightarrow G\operatorname{id}_{\mathsf{D}}\simeq G\end{eqnarray}$$
is equivalent to the identity map. Thus, the co-unit
 $\mathit{FG}\rightarrow \operatorname{id}_{\mathsf{D}}$
is an equivalence, and we conclude the proof.◻
$\mathit{FG}\rightarrow \operatorname{id}_{\mathsf{D}}$
is an equivalence, and we conclude the proof.◻
Let
![]() $\mathsf{D}$
be a small stable
$\mathsf{D}$
be a small stable
![]() $\infty$
-category, admitting finite limits. We will define a functor
$\infty$
-category, admitting finite limits. We will define a functor
 $$\begin{eqnarray}\mathsf{Map}(-,-):\unicode[STIX]{x1D6E5}^{\mathsf{op}}\times \mathsf{D}^{\unicode[STIX]{x1D6E5}}\rightarrow \mathsf{D}^{\unicode[STIX]{x1D6E5}},\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Map}(-,-):\unicode[STIX]{x1D6E5}^{\mathsf{op}}\times \mathsf{D}^{\unicode[STIX]{x1D6E5}}\rightarrow \mathsf{D}^{\unicode[STIX]{x1D6E5}},\end{eqnarray}$$
sending a co-simplicial object
![]() $U^{\bullet }$
in
$U^{\bullet }$
in
![]() $\mathsf{D}$
and
$\mathsf{D}$
and
![]() $[n]\in \unicode[STIX]{x1D6E5}$
to a co-simplicial object
$[n]\in \unicode[STIX]{x1D6E5}$
to a co-simplicial object
 $\mathsf{Map}([n],U^{\bullet })$
. Recall that we have a category
$\mathsf{Map}([n],U^{\bullet })$
. Recall that we have a category
![]() $\unicode[STIX]{x1D6E5}/[n]$
, whose objects are morphisms
$\unicode[STIX]{x1D6E5}/[n]$
, whose objects are morphisms
 $[k]\rightarrow [n]$
. It is endowed with a forgetful functor to
$[k]\rightarrow [n]$
. It is endowed with a forgetful functor to
![]() $\unicode[STIX]{x1D6E5}$
, and this construction is contravariantly functorial in
$\unicode[STIX]{x1D6E5}$
, and this construction is contravariantly functorial in
![]() $[n]$
. The co-simplicial object
$[n]$
. The co-simplicial object
 $\mathsf{Map}([n],U^{\bullet })$
is given by considering the functor
$\mathsf{Map}([n],U^{\bullet })$
is given by considering the functor
 $\unicode[STIX]{x1D6E5}/[n]\rightarrow \unicode[STIX]{x1D6E5}\rightarrow \mathsf{D}$
, and taking the fibrewise limit along
$\unicode[STIX]{x1D6E5}/[n]\rightarrow \unicode[STIX]{x1D6E5}\rightarrow \mathsf{D}$
, and taking the fibrewise limit along
 $\unicode[STIX]{x1D6E5}/[n]\rightarrow \unicode[STIX]{x1D6E5}$
to obtain a functor
$\unicode[STIX]{x1D6E5}/[n]\rightarrow \unicode[STIX]{x1D6E5}$
to obtain a functor
 $\mathsf{Map}([n],U^{\bullet }):\unicode[STIX]{x1D6E5}\rightarrow \mathsf{D}$
.
$\mathsf{Map}([n],U^{\bullet }):\unicode[STIX]{x1D6E5}\rightarrow \mathsf{D}$
.
Definition A.8. Let
 $U^{\bullet },V^{\bullet }:\unicode[STIX]{x1D6E5}\rightarrow \mathsf{D}$
be two co-simplicial objects in a small
$U^{\bullet },V^{\bullet }:\unicode[STIX]{x1D6E5}\rightarrow \mathsf{D}$
be two co-simplicial objects in a small
![]() $\infty$
-category
$\infty$
-category
![]() $\mathsf{D}$
, admitting finite limits. A homotopy between
$\mathsf{D}$
, admitting finite limits. A homotopy between
 $f,g:U^{\bullet }\rightarrow V^{\bullet }$
is a morphism
$f,g:U^{\bullet }\rightarrow V^{\bullet }$
is a morphism
 $h:U^{\bullet }\rightarrow \mathsf{Map}([1],V^{\bullet })$
, such that
$h:U^{\bullet }\rightarrow \mathsf{Map}([1],V^{\bullet })$
, such that
 $\text{ev}_{0}\circ h\simeq f$
and
$\text{ev}_{0}\circ h\simeq f$
and
 $\text{ev}_{1}\circ h\simeq g$
. Here
$\text{ev}_{1}\circ h\simeq g$
. Here
 $\text{ev}_{i}:\mathsf{Map}([1],V^{\bullet })\rightarrow V^{\bullet }$
denotes the evaluation map, induced by the inclusion
$\text{ev}_{i}:\mathsf{Map}([1],V^{\bullet })\rightarrow V^{\bullet }$
denotes the evaluation map, induced by the inclusion
 $[0]\simeq \{i\}{\hookrightarrow}[1]$
.
$[0]\simeq \{i\}{\hookrightarrow}[1]$
.
We refer the reader to [Sta, Tag 019U] for a detailed explanation for how this recovers the explicit definition given earlier, in the case that
![]() $\mathsf{D}$
is a classical category (with small colimits). The reason for considering the notion of homotopy between morphisms of simplicial objects, is the following lemma.
$\mathsf{D}$
is a classical category (with small colimits). The reason for considering the notion of homotopy between morphisms of simplicial objects, is the following lemma.
Lemma A.9. Let
![]() $\mathsf{C}^{\bullet }$
be a co-simplicial small
$\mathsf{C}^{\bullet }$
be a co-simplicial small
![]() $\infty$
-category. Then, the map
$\infty$
-category. Then, the map
 $c:\mathsf{C}^{\bullet }\rightarrow \mathsf{Map}([1],\mathsf{C}^{\bullet })$
, corresponding to the map
$c:\mathsf{C}^{\bullet }\rightarrow \mathsf{Map}([1],\mathsf{C}^{\bullet })$
, corresponding to the map
 $s:[1]\rightarrow [0]$
of simplicial sets, induces an equivalence of the
$s:[1]\rightarrow [0]$
of simplicial sets, induces an equivalence of the
![]() $\infty$
-categories obtained by totalisation
$\infty$
-categories obtained by totalisation
 $|\mathsf{C}^{\bullet }|\rightarrow |\mathsf{Map}([1],\mathsf{C}^{\bullet })|$
. In particular, we see that two homotopy equivalent co-simplicial small
$|\mathsf{C}^{\bullet }|\rightarrow |\mathsf{Map}([1],\mathsf{C}^{\bullet })|$
. In particular, we see that two homotopy equivalent co-simplicial small
![]() $\infty$
-categories have equivalent totalisations.
$\infty$
-categories have equivalent totalisations.
Proof. For co-simplicial objects in the full subcategory of small
![]() $\infty$
-groupoids
$\infty$
-groupoids
![]() $\infty \text{-}\mathsf{Gpd}$
this assertion is well-known, and follows for instance from Meyer’s [Reference MeyerMey90, Theorem 2.4] or Bousfield’s [Reference BousfieldBou03, Proposition 2.13] results. We will apply their result in our proof of the analogous assumption for co-simplicial objects in small
$\infty \text{-}\mathsf{Gpd}$
this assertion is well-known, and follows for instance from Meyer’s [Reference MeyerMey90, Theorem 2.4] or Bousfield’s [Reference BousfieldBou03, Proposition 2.13] results. We will apply their result in our proof of the analogous assumption for co-simplicial objects in small
![]() $\infty$
-categories. We will show first that the functor
$\infty$
-categories. We will show first that the functor
 $|c|:|\mathsf{C}^{\bullet }|{\hookrightarrow}|\mathsf{Map}([1],\mathsf{C}^{\bullet })|$
is fully faithful. Given
$|c|:|\mathsf{C}^{\bullet }|{\hookrightarrow}|\mathsf{Map}([1],\mathsf{C}^{\bullet })|$
is fully faithful. Given
 $X,Y\in |\mathsf{C}^{\bullet }|$
, we recall Lemma A.2, which asserts that
$X,Y\in |\mathsf{C}^{\bullet }|$
, we recall Lemma A.2, which asserts that
 $\mathsf{Map}(X,Y)$
is itself the totalisation of a co-simplicial object in
$\mathsf{Map}(X,Y)$
is itself the totalisation of a co-simplicial object in
![]() $\infty \text{-}\mathsf{Gpd}$
,
$\infty \text{-}\mathsf{Gpd}$
,
 $\mathsf{Map}(X^{\bullet },Y^{\bullet })$
. It follows directly from the definitions that
$\mathsf{Map}(X^{\bullet },Y^{\bullet })$
. It follows directly from the definitions that
 $\mathsf{Map}(c(X)^{\bullet },c(Y)^{\bullet })\simeq |\mathsf{Map}([1],\mathsf{Map}(X^{\bullet },Y^{\bullet }))|$
. We may therefore conclude that
$\mathsf{Map}(c(X)^{\bullet },c(Y)^{\bullet })\simeq |\mathsf{Map}([1],\mathsf{Map}(X^{\bullet },Y^{\bullet }))|$
. We may therefore conclude that
 $\mathsf{Map}(X,Y)\simeq \mathsf{Map}(c(X),c(Y))$
, and thus that
$\mathsf{Map}(X,Y)\simeq \mathsf{Map}(c(X),c(Y))$
, and thus that
![]() $c$
is fully faithful. It remains to show that
$c$
is fully faithful. It remains to show that
![]() $c$
is essentially surjective. For a small
$c$
is essentially surjective. For a small
![]() $\infty$
-category
$\infty$
-category
![]() $\mathsf{D}$
, we denote by
$\mathsf{D}$
, we denote by
![]() $\mathsf{D}^{\times }$
the maximal
$\mathsf{D}^{\times }$
the maximal
![]() $\infty$
-groupoid in
$\infty$
-groupoid in
![]() $\mathsf{D}$
, obtained by discarding all non-equivalences in
$\mathsf{D}$
, obtained by discarding all non-equivalences in
![]() $\mathsf{D}$
. In fact, we have a functor
$\mathsf{D}$
. In fact, we have a functor
 $(-)^{\times }:\infty \text{-}\mathsf{Cat}\rightarrow \infty \text{-}\mathsf{Gpd}$
. We therefore see, that the morphism of co-simplicial objects in
$(-)^{\times }:\infty \text{-}\mathsf{Cat}\rightarrow \infty \text{-}\mathsf{Gpd}$
. We therefore see, that the morphism of co-simplicial objects in
![]() $\infty \text{-}\mathsf{Gpd}$
,
$\infty \text{-}\mathsf{Gpd}$
,
 $c^{\times }:(\mathsf{C}^{\bullet })^{\times }\rightarrow \mathsf{Map}([1],\mathsf{C}^{\bullet })^{\times }\simeq \mathsf{Map}([1],(\mathsf{C}^{\bullet })^{\times })$
induces an equivalence after totalisation. This implies that
$c^{\times }:(\mathsf{C}^{\bullet })^{\times }\rightarrow \mathsf{Map}([1],\mathsf{C}^{\bullet })^{\times }\simeq \mathsf{Map}([1],(\mathsf{C}^{\bullet })^{\times })$
induces an equivalence after totalisation. This implies that
![]() $c$
is essentially surjective.◻
$c$
is essentially surjective.◻
Appendix B Notation
-
 $|X|$
$|X|$
-
underlying topological space of a scheme
 $X$
$X$
-
 $|X|_{{\leqslant}}$
$|X|_{{\leqslant}}$
-
partially ordered set of points in
 $|X|$
ordered by specialisation
$|X|$
ordered by specialisation -
 $|X|_{\bullet }$
$|X|_{\bullet }$
-
simplicial set of chains of points in
 $|X|$
, ordered by specialisation
$|X|$
, ordered by specialisation -
 $\mathbb{A}_{X}^{\bullet }$
$\mathbb{A}_{X}^{\bullet }$
-
co-simplicial ring of adèles
-
 $\mathsf{A}_{X}^{\bullet }$
$\mathsf{A}_{X}^{\bullet }$
-
co-simplicial sheaf of algebras of adèles
-
 $\mathsf{A}_{X,T}({\mathcal{F}})$
$\mathsf{A}_{X,T}({\mathcal{F}})$
-
the value of the functor of Definition 1.4 applied to a quasi-coherent sheaf
 $F$
$F$
-
 $\mathsf{A}_{X,T}^{k}$
$\mathsf{A}_{X,T}^{k}$
-
the value of the functor above applied to
 ${\mathcal{O}}_{X}$
and
${\mathcal{O}}_{X}$
and
 $T=|X|_{k}$
$T=|X|_{k}$
-
 $\mathsf{Sch}^{\mathsf{N}}$
$\mathsf{Sch}^{\mathsf{N}}$
-
category of Noetherian schemes
-
 $\mathsf{Sch}^{\mathsf{qcqs}}$
$\mathsf{Sch}^{\mathsf{qcqs}}$
-
category of quasi-compact and quasi-separated schemes
-
 $BG$
$BG$
-
stack of
 $G$
-bundles
$G$
-bundles -
 $\mathsf{Mod}(R)$
$\mathsf{Mod}(R)$
-
category of
 $R$
-modules, where
$R$
-modules, where
 $R$
is a ring or a sheaf of rings
$R$
is a ring or a sheaf of rings -
 $\mathsf{P}(R)$
$\mathsf{P}(R)$
-
exact category of projective
 $R$
-modules (
$R$
-modules (
 $R$
is a ring)
$R$
is a ring) -
 $\mathsf{P}(\mathsf{A})$
$\mathsf{P}(\mathsf{A})$
-
exact category of direct summands of free
 $\mathsf{A}$
-modules (
$\mathsf{A}$
-modules (
 $\mathsf{A}$
is a sheaf of algebras)
$\mathsf{A}$
is a sheaf of algebras) -
 $\mathsf{D}^{-}(\mathsf{A})$
$\mathsf{D}^{-}(\mathsf{A})$
-
see Definition 2.18
-
 $\mathsf{D}(\mathsf{C})$
$\mathsf{D}(\mathsf{C})$
-
derived
 $\infty$
-category of an exact category
$\infty$
-category of an exact category
 $\mathsf{C}$
$\mathsf{C}$
-
 $\mathsf{DMod}(\mathsf{A})$
$\mathsf{DMod}(\mathsf{A})$
-
derived
 $\infty$
-category of
$\infty$
-category of
 $\mathsf{Mod}(\mathsf{A})$
, where
$\mathsf{Mod}(\mathsf{A})$
, where
 $\mathsf{A}$
is a ring or a sheaf of algebras
$\mathsf{A}$
is a ring or a sheaf of algebras -
 $\mathsf{Perf}(\mathsf{A})$
$\mathsf{Perf}(\mathsf{A})$
-
full subcategory of
 $\mathsf{DMod}(\mathsf{A})$
consisting of perfect complexes
$\mathsf{DMod}(\mathsf{A})$
consisting of perfect complexes -
 $\mathsf{Perf}_{|Z|}(\mathsf{A})$
$\mathsf{Perf}_{|Z|}(\mathsf{A})$
-
full subcategory of
 $\mathsf{Perf}(\mathsf{A})$
consisting of perfect complexes set-theoretically supported on a closed subset
$\mathsf{Perf}(\mathsf{A})$
consisting of perfect complexes set-theoretically supported on a closed subset
 $|Z|$
$|Z|$
-
 $\mathsf{QC}(\mathsf{A})$
$\mathsf{QC}(\mathsf{A})$
-
 $\mathsf{Ind}\mathsf{Perf}(\mathsf{A})$
, if
$\mathsf{Ind}\mathsf{Perf}(\mathsf{A})$
, if
 $\mathsf{A}$
is a ring (on a point), it is equivalent to
$\mathsf{A}$
is a ring (on a point), it is equivalent to
 $\mathsf{DMod}(\mathsf{A})$
$\mathsf{DMod}(\mathsf{A})$
-
 $\mathsf{QC}_{|Z|}(\mathsf{A})$
$\mathsf{QC}_{|Z|}(\mathsf{A})$
-
full subcategory of
 $\mathsf{QC}(\mathsf{A})$
consisting of complexes set-theoretically supported on a closed subset
$\mathsf{QC}(\mathsf{A})$
consisting of complexes set-theoretically supported on a closed subset
 $|Z|$
$|Z|$
-
 $\mathsf{QC}(X)$
$\mathsf{QC}(X)$
-
 $\mathsf{QC}({\mathcal{O}}_{X})$
if
$\mathsf{QC}({\mathcal{O}}_{X})$
if
 $X$
is quasi-compact and quasi-separated, see Remarks 3.4 and 3.34 for more general definitions
$X$
is quasi-compact and quasi-separated, see Remarks 3.4 and 3.34 for more general definitions -
 $\mathsf{C}^{\text{c}}$
$\mathsf{C}^{\text{c}}$
-
full subcategory of compact objects of a stable
 $\infty$
-category
$\infty$
-category
 $\mathsf{C}$
$\mathsf{C}$
-
 $\mathsf{APerf}(\mathsf{A})$
$\mathsf{APerf}(\mathsf{A})$
-
full subcategory of
 $\mathsf{QC}(\mathsf{A})$
corresponding to pseudo-coherent complexes
$\mathsf{QC}(\mathsf{A})$
corresponding to pseudo-coherent complexes -
 $\infty \text{-}\mathsf{Cat}$
$\infty \text{-}\mathsf{Cat}$
-
 $\infty$
-category of small
$\infty$
-category of small
 $\infty$
-categories
$\infty$
-categories -
 $\mathsf{Cat}$
$\mathsf{Cat}$
-
2-category of small categories
-
 $\infty \text{-}\mathsf{Gpd}$
$\infty \text{-}\mathsf{Gpd}$
-
 $\infty$
-category of small
$\infty$
-category of small
 $\infty$
-groupoids, Kan complexes or spaces
$\infty$
-groupoids, Kan complexes or spaces -
 $\mathsf{Grpd}$
$\mathsf{Grpd}$
-
2-category of groupoids
-
 $\mathsf{st}$
$\mathsf{st}$
-
 $\infty$
-category of small stable
$\infty$
-category of small stable
 $\infty$
-categories
$\infty$
-categories -
 $\mathsf{Map}_{\mathsf{C}}(X,Y)$
$\mathsf{Map}_{\mathsf{C}}(X,Y)$
-
mapping space between two objects
 $X,Y$
in an
$X,Y$
in an
 $\infty$
-category
$\infty$
-category
 $\mathsf{C}$
$\mathsf{C}$
-
 $\mathsf{Hom}_{\mathsf{C}}(X,Y)$
$\mathsf{Hom}_{\mathsf{C}}(X,Y)$
-
mapping spectrum between two objects
 $X,Y$
in a stable
$X,Y$
in a stable
 $\infty$
-category
$\infty$
-category
 $\mathsf{C}$
, or chain complex, if
$\mathsf{C}$
, or chain complex, if
 $\mathsf{C}$
is
$\mathsf{C}$
is
 $R$
-linear
$R$
-linear -
 $(-)_{\otimes }$
$(-)_{\otimes }$
-
subscript used to refer to symmetric monoidal
 $\infty$
-categories or also
$\infty$
-categories or also
 $\infty$
-categories of symmetric monoidal
$\infty$
-categories of symmetric monoidal
 $\infty$
-categories
$\infty$
-categories -
 $|X^{\bullet }|$
$|X^{\bullet }|$
-
limit (that is, geometric realisation, or totalisation) of the co-simplicial diagram
 $X^{\bullet }$
in an
$X^{\bullet }$
in an
 $\infty$
-category
$\infty$
-category
 $\mathsf{C}$
$\mathsf{C}$
-
 $|X_{\bullet }|$
$|X_{\bullet }|$
-
colimit (that is, geometric realisation, or totalisation) of the simplicial diagram
 $X_{\bullet }$
in an
$X_{\bullet }$
in an
 $\infty$
-category
$\infty$
-category
 $\mathsf{C}$
$\mathsf{C}$
-
 $\simeq$
$\simeq$
-
denotes an equivalence of two objects in an
 $\infty$
-category, including the special case of an equivalence of two small
$\infty$
-category, including the special case of an equivalence of two small
 $\infty$
-categories
$\infty$
-categories