Article contents
Stable homotopy refinement of quantum annular homology
Published online by Cambridge University Press: 08 April 2021
Abstract
We construct a stable homotopy refinement of quantum annular homology, a link homology theory introduced by Beliakova, Putyra and Wehrli. For each 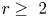 $r\geq ~2$ we associate to an annular link
$r\geq ~2$ we associate to an annular link 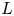 $L$ a naive
$L$ a naive 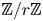 $\mathbb {Z}/r\mathbb {Z}$-equivariant spectrum whose cohomology is isomorphic to the quantum annular homology of
$\mathbb {Z}/r\mathbb {Z}$-equivariant spectrum whose cohomology is isomorphic to the quantum annular homology of 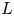 $L$ as modules over
$L$ as modules over 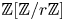 $\mathbb {Z}[\mathbb {Z}/r\mathbb {Z}]$. The construction relies on an equivariant version of the Burnside category approach of Lawson, Lipshitz and Sarkar. The quotient under the cyclic group action is shown to recover the stable homotopy refinement of annular Khovanov homology. We study spectrum level lifts of structural properties of quantum annular homology.
$\mathbb {Z}[\mathbb {Z}/r\mathbb {Z}]$. The construction relies on an equivariant version of the Burnside category approach of Lawson, Lipshitz and Sarkar. The quotient under the cyclic group action is shown to recover the stable homotopy refinement of annular Khovanov homology. We study spectrum level lifts of structural properties of quantum annular homology.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2021
Footnotes
R.A. was supported by NSF RTG Grant DMS-1839968, V.K. was supported by NSF Grant DMS-1612159, and M.W. was supported by NSF FRG Grant DMS-1563615.
References
- 2
- Cited by





