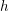Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
del Pino, Álvaro
and
Vogel, Thomas
2020.
The Engel–Lutz twist and overtwisted Engel
structures.
Geometry & Topology,
Vol. 24,
Issue. 5,
p.
2471.
Haller, Stefan
2022.
Analytic Torsion of Generic Rank Two Distributions in Dimension Five.
The Journal of Geometric Analysis,
Vol. 32,
Issue. 10,
Cardona, Robert
Miranda, Eva
Peralta-Salas, Daniel
and
Presas, Francisco
2023.
Universality of Euler flows and flexibility of Reeb embeddings.
Advances in Mathematics,
Vol. 428,
Issue. ,
p.
109142.
Cardona, Robert
and
Presas, Francisco
2024.
An h$h$‐principle for embeddings transverse to a contact structure.
Journal of Topology,
Vol. 17,
Issue. 1,