Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chen, Qile
Janda, Felix
and
Ruan, Yongbin
2021.
The logarithmic gauged linear sigma model.
Inventiones mathematicae,
Vol. 225,
Issue. 3,
p.
1077.
Bousseau, Pierrick
2021.
Scattering Diagrams, Sheaves, and Curves.
Acta Mathematica Sinica, English Series,
Vol. 37,
Issue. 7,
p.
1005.
Ulirsch, Martin
2021.
A non-Archimedean analogue of Teichmüller space and its tropicalization.
Selecta Mathematica,
Vol. 27,
Issue. 3,
Farajzadeh-Tehrani, Mohammad
2022.
Limits of stable maps in a semi-stable degeneration.
Geometriae Dedicata,
Vol. 216,
Issue. 6,
Farajzadeh-Tehrani, Mohammad
2022.
Pseudoholomorphic curves relative to a normal crossings symplectic divisor: compactification.
Geometry & Topology,
Vol. 26,
Issue. 3,
p.
989.
Barrott, Lawrence Jack
and
Nabijou, Navid
2022.
Tangent curves to degenerating hypersurfaces.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2022,
Issue. 793,
p.
185.
Gross, Mark
and
Siebert, Bernd
2022.
The canonical wall structure and intrinsic mirror symmetry.
Inventiones mathematicae,
Vol. 229,
Issue. 3,
p.
1101.
Argüz, Hülya
and
Bousseau, Pierrick
2022.
Real Log Curves in Toric Varieties, Tropical Curves, and Log Welschinger Invariants.
Annales de l'Institut Fourier,
Vol. 72,
Issue. 4,
p.
1547.
Argüz, Hülya
and
Gross, Mark
2022.
The higher-dimensional tropical vertex.
Geometry & Topology,
Vol. 26,
Issue. 5,
p.
2135.
Graefnitz, Tim
2022.
Tropical correspondence for smooth del Pezzo log Calabi-Yau pairs.
Journal of Algebraic Geometry,
Vol. 31,
Issue. 4,
p.
687.
Bousseau, Pierrick
2023.
A proof of N. Takahashi’s conjecture for (P2,E) and a refined sheaves/Gromov–Witten correspondence.
Duke Mathematical Journal,
Vol. 172,
Issue. 15,
Bousseau, Pierrick
2023.
Strong Positivity for the Skein Algebras of the 4-Punctured Sphere and of the 1-Punctured Torus.
Communications in Mathematical Physics,
Vol. 398,
Issue. 1,
p.
1.
Chen, Qile
Janda, Felix
Ruan, Yongbin
and
Sauvaget, Adrien
2023.
Towards logarithmic GLSM : the r–spin
case.
Geometry & Topology,
Vol. 26,
Issue. 7,
p.
2855.
Cavalieri, Renzo
Markwig, Hannah
and
Ranganathan, Dhruv
2023.
Tropical and Logarithmic Methods in Enumerative Geometry.
Vol. 52,
Issue. ,
p.
39.
Wu, Yixian
2023.
Splitting of Gromov–Witten invariants with toric gluing strata.
Journal of Algebraic Geometry,
Vol. 33,
Issue. 2,
p.
213.
Tseng, Hsian-Hua
and
You, Fenglong
2023.
A Gromov–Witten Theory for Simple Normal-Crossing Pairs Without Log Geometry.
Communications in Mathematical Physics,
Vol. 401,
Issue. 1,
p.
803.
Blomme, Thomas
2023.
Tropical curves in abelian surfaces II: Enumeration of curves in linear systems.
Transactions of the American Mathematical Society,
Vol. 376,
Issue. 8,
p.
5641.
Kim, Bumsig
Lho, Hyenho
and
Ruddat, Helge
2023.
The degeneration formula for stable log maps.
manuscripta mathematica,
Vol. 170,
Issue. 1-2,
p.
63.
Christ, Karl
He, Xiang
and
Tyomkin, Ilya
2023.
On the Severi problem in arbitrary characteristic.
Publications mathématiques de l'IHÉS,
Vol. 137,
Issue. 1,
p.
1.
ARGÜZ, HÜLYA
2023.
Equations of mirrors to log Calabi–Yau pairs via the heart of canonical wall structures.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 175,
Issue. 2,
p.
381.
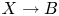 $X \longrightarrow B$ with singular fibre over
$X \longrightarrow B$ with singular fibre over 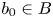 $b_0\in B$ yields a family
$b_0\in B$ yields a family 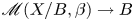 $\mathscr {M}(X/B,\beta ) \longrightarrow B$ of moduli stacks of stable logarithmic maps. We give a virtual decomposition of the fibre of this family over
$\mathscr {M}(X/B,\beta ) \longrightarrow B$ of moduli stacks of stable logarithmic maps. We give a virtual decomposition of the fibre of this family over 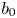 $b_0$ in terms of rigid tropical maps to the tropicalization of
$b_0$ in terms of rigid tropical maps to the tropicalization of 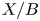 $X/B$. This generalizes one aspect of known results in the case that the fibre
$X/B$. This generalizes one aspect of known results in the case that the fibre 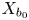 $X_{b_0}$ is a normal crossings union of two divisors. We exhibit our formulas in explicit examples.
$X_{b_0}$ is a normal crossings union of two divisors. We exhibit our formulas in explicit examples.




