Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Liu, Chun-Hung
and
Oum, Sang-il
2015.
Partitioning H -minor free graphs into three subgraphs with no large components.
Electronic Notes in Discrete Mathematics,
Vol. 49,
Issue. ,
p.
133.
Esperet, Louis
and
Ochem, Pascal
2016.
Islands in Graphs on Surfaces.
SIAM Journal on Discrete Mathematics,
Vol. 30,
Issue. 1,
p.
206.
Gimbel, John
2016.
Graph Theory.
p.
95.
Axenovich, Maria
Ueckerdt, Torsten
and
Weiner, Pascal
2017.
Splitting Planar Graphs of Girth 6 into Two Linear Forests with Short Paths.
Journal of Graph Theory,
Vol. 85,
Issue. 3,
p.
601.
Liu, Chun-Hung
and
Oum, Sang-il
2018.
Partitioning H-minor free graphs into three subgraphs with no large components.
Journal of Combinatorial Theory, Series B,
Vol. 128,
Issue. ,
p.
114.
van den Heuvel, Jan
and
Wood, David R.
2018.
Improper colourings inspired by Hadwiger's conjecture.
Journal of the London Mathematical Society,
Vol. 98,
Issue. 1,
p.
129.
Keszegh, Balázs
and
Pálvölgyi, Dömötör
2019.
Proper Coloring of Geometric Hypergraphs.
Discrete & Computational Geometry,
Vol. 62,
Issue. 3,
p.
674.
Kang, Dong Yeap
and
Oum, Sang-Il
2019.
Improper colouring of graphs with no odd clique minor.
Combinatorics, Probability and Computing,
Vol. 28,
Issue. 5,
p.
740.
Dujmović, Vida
Eppstein, David
Joret, Gwenaël
Morin, Pat
and
Wood, David R.
2020.
Minor-Closed Graph Classes with Bounded Layered Pathwidth.
SIAM Journal on Discrete Mathematics,
Vol. 34,
Issue. 3,
p.
1693.
Damásdi, Gábor
and
Pálvölgyi, Dömötör
2022.
Realizing an m-Uniform Four-Chromatic Hypergraph with Disks.
Combinatorica,
Vol. 42,
Issue. S1,
p.
1027.
Liu, Chun-Hung
and
Wood, David R.
2022.
Clustered variants of Hajós' conjecture.
Journal of Combinatorial Theory, Series B,
Vol. 152,
Issue. ,
p.
27.
Dujmović, Vida
Esperet, Louis
Morin, Pat
Walczak, Bartosz
and
Wood, David R.
2022.
Clustered 3-colouring graphs of bounded degree.
Combinatorics, Probability and Computing,
Vol. 31,
Issue. 1,
p.
123.
Liu, Chun-Hung
and
Wood, David R.
2023.
Clustered coloring of graphs with bounded layered treewidth and bounded degree.
European Journal of Combinatorics,
p.
103730.
Norin, Sergey
Scott, Alex
and
Wood, David R.
2023.
Clustered colouring of graph classes with bounded treedepth or pathwidth.
Combinatorics, Probability and Computing,
Vol. 32,
Issue. 1,
p.
122.
Dvořák, Zdeněk
and
Norin, Sergey
2023.
Weak diameter coloring of graphs on surfaces.
European Journal of Combinatorics,
p.
103845.
Esperet, Louis
and
Wood, David R.
2023.
Colouring strong products.
European Journal of Combinatorics,
p.
103847.
Campbell, Rutger
Clinch, Katie
Distel, Marc
Gollin, J. Pascal
Hendrey, Kevin
Hickingbotham, Robert
Huynh, Tony
Illingworth, Freddie
Tamitegama, Youri
Tan, Jane
and
Wood, David R.
2024.
Product structure of graph classes with bounded treewidth.
Combinatorics, Probability and Computing,
Vol. 33,
Issue. 3,
p.
351.
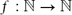 $f :\mathbb{N} \to \mathbb{N}$ such that the vertices of every planar graph with maximum degree Δ can be 3-coloured in such a way that each monochromatic component has at most f(Δ) vertices. This is best possible (the number of colours cannot be reduced and the dependence on the maximum degree cannot be avoided) and answers a question raised by Kleinberg, Motwani, Raghavan and Venkatasubramanian in 1997. Our result extends to graphs of bounded genus.
$f :\mathbb{N} \to \mathbb{N}$ such that the vertices of every planar graph with maximum degree Δ can be 3-coloured in such a way that each monochromatic component has at most f(Δ) vertices. This is best possible (the number of colours cannot be reduced and the dependence on the maximum degree cannot be avoided) and answers a question raised by Kleinberg, Motwani, Raghavan and Venkatasubramanian in 1997. Our result extends to graphs of bounded genus.



