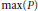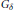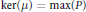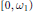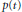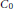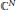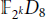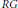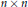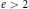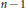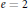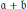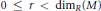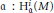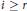Research Article
Measurements and Gδ-Subsets of Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 193-206
-
- Article
-
- You have access
- Export citation
Irreducible Representations of Inner Quasidiagonal C*-Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 385-395
-
- Article
-
- You have access
- Export citation
Extensions of Positive Definite Functions on Amenable Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-11
-
- Article
-
- You have access
- Export citation
Erratum: The Duality Problem For The Class of AM-Compact Operators On Banach Lattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 577-579
-
- Article
-
- You have access
- Export citation
A Bilinear Fractional Integral on Compact Lie Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 207-216
-
- Article
-
- You have access
- Export citation
Parabolic Geodesics in Sasakian 3-Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 396-410
-
- Article
-
- You have access
- Export citation
Kiguradze-type Oscillation Theorems for Second Order Superlinear Dynamic Equations on Time Scales
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 580-592
-
- Article
-
- You have access
- Export citation
Homotopy and the Kestelman–Borwein–Ditor Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 12-20
-
- Article
-
- You have access
- Export citation
Recurrence Relations for Strongly q-Log-Convex Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 217-229
-
- Article
-
- You have access
- Export citation
Generalized D-symmetric Operators II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 21-27
-
- Article
-
- You have access
- Export citation
Award Winners
Research Article
Operator Algebras with Unique Preduals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 411-421
-
- Article
-
- You have access
- Export citation
Research Article
Stability of Real C*-Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 593-606
-
- Article
-
- You have access
- Export citation
Lightness of Induced Maps and Homeomorphisms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 607-618
-
- Article
-
- You have access
- Export citation
Generalized Solution of the Photon Transport Problem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 28-38
-
- Article
-
- You have access
- Export citation
Universal Power Series in ℂN
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 230-236
-
- Article
-
- You have access
- Export citation
Two Conditions on the Structure Jacobi Operator for Real Hypersurfaces in Complex Projective Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 422-429
-
- Article
-
- You have access
- Export citation
Elements in a Numerical Semigroup with Factorizations of the Same Length
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 39-43
-
- Article
-
- You have access
- Export citation
The Structure of the Unit Group of the Group Algebra
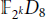
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 237-243
-
- Article
-
- You have access
- Export citation
Complete Families of Linearly Non-degenerate Rational Curves
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 430-441
-
- Article
-
- You have access
- Export citation
Artinian and Non-Artinian Local Cohomology Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 619-629
-
- Article
-
- You have access
- Export citation