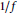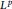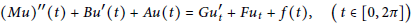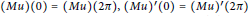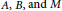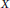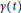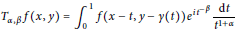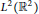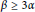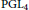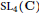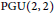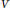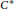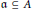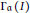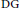Research Article
Relative Equilibria in Curved Restricted 4-body Problems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-687
-
- Article
-
- You have access
- Export citation
The Universal Enveloping Algebra of the Schrödinger Algebra and its Prime Spectrum
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 688-703
-
- Article
-
- You have access
- Export citation
Remarks on Inner Functions and Optimal Approximants
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 704-716
-
- Article
-
- You have access
- Export citation
Periodic Solutions of Second Order Degenerate Differential Equations with Delay in Banach Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 717-737
-
- Article
-
- You have access
- Export citation
Poincaré Inequalities and Neumann Problems for the p-Laplacian
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 738-753
-
- Article
-
- You have access
- Export citation
A note on concordance properties of fibers in Seifert homology spheres
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 754-767
-
- Article
-
- You have access
- Export citation
Chaotic Vibration of a Two-dimensional Non-strictly Hyperbolic Equation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 768-786
-
- Article
-
- You have access
- Export citation
Endpoint Estimates of Riesz Transforms Associated with Generalized Schrödinger Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 787-801
-
- Article
-
- You have access
- Export citation
The Oscillatory Hyper-Hilbert Transform Associated with Plane Curves
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 802-811
-
- Article
-
- You have access
- Export citation
Infinite Powers and Cohen Reals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 812-821
-
- Article
-
- You have access
- Export citation
Multivariate Rankin–Selberg Integrals on GL4 and GU(2, 2)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 822-835
-
- Article
-
- You have access
- Export citation
Total Nonnegativity and Stable Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 836-847
-
- Article
-
- You have access
- Export citation
Quantum Symmetries of Graph C*-algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 848-864
-
- Article
-
- You have access
- Export citation
Homological Dimensions of Local (Co)homology Over Commutative DG-rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 865-877
-
- Article
-
- You have access
- Export citation
Weak Approximation for Points with Coordinates in Rank-one Subgroups of Global Function Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 878-890
-
- Article
-
- You have access
- Export citation