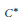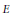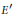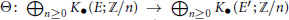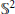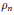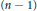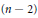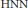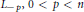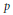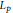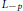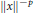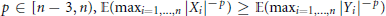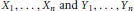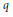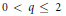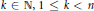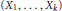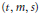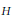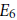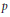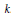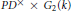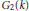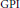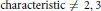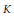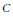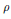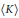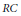Research Article
Homotopy of Knots and the Alexander Polynomial
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 257-262
-
- Article
-
- You have access
- Export citation
Mellin Transforms of Mixed Cusp Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 263-273
-
- Article
-
- You have access
- Export citation
The Bockstein Map is Necessary
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 274-284
-
- Article
-
- You have access
- Export citation
On Kloosterman Sums with Oscillating Coefficients
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 285-290
-
- Article
-
- You have access
- Export citation
Spaces of Quasi-Measures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 291-297
-
- Article
-
- You have access
- Export citation
Semigroup Algebras and Maximal Orders
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 298-306
-
- Article
-
- You have access
- Export citation
On the Moduli Space of a Spherical Polygonal Linkage
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 307-320
-
- Article
-
- You have access
- Export citation
Averaging Operators and Martingale Inequalities in Rearrangement Invariant Function Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 321-334
-
- Article
-
- You have access
- Export citation
Cyclic Subgroup Separability of HNN-Extensions with Cyclic Associated Subgroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 335-343
-
- Article
-
- You have access
- Export citation
Positive Definite Distributions and Subspaces of L_p With Applications to Stable Processes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 344-353
-
- Article
-
- You have access
- Export citation
A Real Holomorphy Ring without the Schmüdgen Property
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 354-358
-
- Article
-
- You have access
- Export citation
A Generalized Rao Bound for Ordered Orthogonal Arrays and (t, m, s)-Nets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 359-370
-
- Article
-
- You have access
- Export citation
Prime and Primary Ideals in a Prüfer Order in a Simple Artinian Ring with Finite Dimension over its Center
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 371-379
-
- Article
-
- You have access
- Export citation
Asymptotic Behavior of Optimal Circle Packings in a Square
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 380-385
-
- Article
-
- You have access
- Export citation
Minimal Separators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 386-392
-
- Article
-
- You have access
- Export citation
A Class of Supercuspidal Representations of G2(k)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 393-400
-
- Article
-
- You have access
- Export citation
Lie Derivations in Prime Rings With Involution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 401-411
-
- Article
-
- You have access
- Export citation
Peirce Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 412-416
-
- Article
-
- You have access
- Export citation