Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-18T23:08:45.939Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Limiting Weak-type Behaviors for Maximal Operators Associated with Power Weighted Measure

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  07 January 2019

Xianming Hou  and
Huoxiong Wu
Xianming Hou
Affiliation:
School of Mathematical Sciences, Xiamen University, Xiamen 361005, China Email: houxianming37@163.comhuoxwu@xmu.edu.cn
Huoxiong Wu
Affiliation:
School of Mathematical Sciences, Xiamen University, Xiamen 361005, China Email: houxianming37@163.comhuoxwu@xmu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 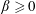$\unicode[STIX]{x1D6FD}\geqslant 0$, let 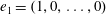$e_{1}=(1,0,\ldots ,0)$ be a unit vector on 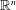$\mathbb{R}^{n}$, and let 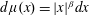$d\unicode[STIX]{x1D707}(x)=|x|^{\unicode[STIX]{x1D6FD}}dx$ be a power weighted measure on 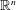$\mathbb{R}^{n}$. For 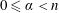$0\leqslant \unicode[STIX]{x1D6FC}<n$, let 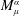$M_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D6FC}}$ be the centered Hardy-Littlewood maximal function and fractional maximal functions associated with measure 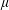$\unicode[STIX]{x1D707}$. This paper shows that for 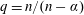$q=n/(n-\unicode[STIX]{x1D6FC})$, 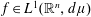$f\in L^{1}(\mathbb{R}^{n},d\unicode[STIX]{x1D707})$,

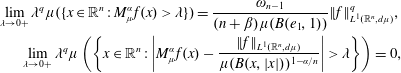$$\begin{eqnarray}\displaystyle \lim _{\unicode[STIX]{x1D706}\rightarrow 0+}\unicode[STIX]{x1D706}^{q}\unicode[STIX]{x1D707}(\{x\in \mathbb{R}^{n}:M_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D6FC}}f(x)>\unicode[STIX]{x1D706}\})=\frac{\unicode[STIX]{x1D714}_{n-1}}{(n+\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D707}(B(e_{1},1))}\Vert f\Vert _{L^{1}(\mathbb{R}^{n},d\unicode[STIX]{x1D707})}^{q}, & & \displaystyle \nonumber\\ \displaystyle \lim _{\unicode[STIX]{x1D706}\rightarrow 0+}\unicode[STIX]{x1D706}^{q}\unicode[STIX]{x1D707}\left(\left\{x\in \mathbb{R}^{n}:\left|M_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D6FC}}f(x)-\frac{\Vert f\Vert _{L^{1}(\mathbb{R}^{n},d\unicode[STIX]{x1D707})}}{\unicode[STIX]{x1D707}(B(x,|x|))^{1-\unicode[STIX]{x1D6FC}/n}}\right|>\unicode[STIX]{x1D706}\right\}\right)=0, & & \displaystyle \nonumber\end{eqnarray}$$
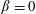which is new and stronger than the previous result even if $\unicode[STIX]{x1D6FD}=0$. Meanwhile, the corresponding results for the un-centered maximal functions as well as the fractional integral operators with respect to measure 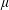$\unicode[STIX]{x1D707}$ are also obtained.

Keywords

limiting weak type behaviorpower weightHardy-Littlewood maximal operatorfractional maximal operatorfractional integral

MSC classification

Primary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Secondary: 42B25: Maximal functions, Littlewood-Paley theory
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 2 , June 2019 , pp. 313 - 326
Copyright
© Canadian Mathematical Society 2018 

Footnotes

Supported by the NNSF of China (Nos. 11771358, 11471041) and the NSF of Fujian Province of China (No. 2015J01025). Huoxiong Wu is the corresponding author.

References

Coifman, R. and Weiss, G., Analyse harmonique non-commutative sur certains espaces homogènes . Lecture Note in Mathematics, 242, Springer-Verlag, Berlin-New York, 1971.Google Scholar
Ding, Y. and Lai, X., L 1-Dini conditions and limiting behavior of weak type estimates for singular integrals . Rev. Mat. Iberoam. 33(2017), no. 4, 1267–1284. https://doi.org/10.4171/RMI/971.Google Scholar
Ding, Y. and Lai, X., Weak type (1, 1) behavior for the maximal operator with L 1-Dini kernel . Potential Anal. 47(2017), no. 2, 169–187. https://doi.org/10.1007/s11118-017-9612-3.Google Scholar
Gatto, A., Gutiérrez, C., and Wheeden, R., On weighted fractional integrals. In: Conference on harmonic analysis in honor of Antoni Zygmund, Vol. I, II (Chicago, III, 1981), Wadsworth Math. Ser., Wadsworth, Belmont, CA, 1983, pp. 124–137.Google Scholar
Heinonen, J., Lectures on analysis on metric spaces, Universitext, Springer-Verlag, New York, 2001. https://doi.org/10.1007/978-1-4613-0131-8.Google Scholar
Hu, J. and Huang, X., A note on the limiting weak-type behavior for maximal operators . Proc. Amer. Math. Soc. 136(2008), 1599–1607. https://doi.org/10.1090/S0002-9939-08-09313-1.Google Scholar
Janakiraman, P., Limiting weak-type behavior for singular integral and maximal operators . Trans. Amer. Math. Soc. 358(2006), no. 5, 1937–1952. https://doi.org/10.1090/S0002-9947-05-04097-3.Google Scholar
Pan, W. J., Fractional integrals on spaces of homogeneous type . Approx. Theory Appl. 8(1992), 1–15.Google Scholar