Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-06-28T20:15:33.412Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Normal Form of the Orthogonal Transformation III

Published online by Cambridge University Press:  20 November 2018

Hans Zassenhaus
Hans Zassenhaus*
Affiliation:
McGill University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Under the assumptions of case of theorem 1 we derive from (3.32) the matrix equation

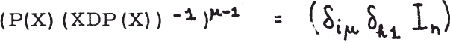
so that there corresponds the matrix B to the bilinear form

4.1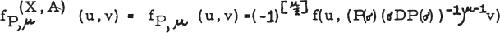

on the linear space

4.2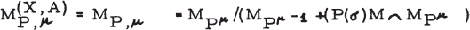

and fP,μ, is symmetric if ɛ = (-1)μ+1, anti-symmetric if ɛ = (-1)μ.

The last statement remains true in the case a) if P is symmetric irreducible because in that case fP,μ is 0.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 1 , Issue 3 , 01 September 1958 , pp. 183 - 191
Copyright
Copyright © Canadian Mathematical Society 1958

References

Dickson, L.E., Linear groups, (Leipzig, 1901).Google Scholar
Dieudonné, J., Sur les groupes classiques, (Paris, 1948).Google Scholar