Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-27T11:19:20.827Z Has data issue: false hasContentIssue false
  • English
  • Français

Ground State and Multiple Solutions for Kirchhoff Type Equations With Critical Exponent

Published online by Cambridge University Press:  20 November 2018

Dongdong Qin ,
Yubo He  and
Xianhua Tang
Dongdong Qin
Affiliation:
School of Mathematics and Statistics, Central South University, Changsha, 410083 Hunan, P.R.China, e-mail: qindd132@163.com
Yubo He
Affiliation:
Department of Mathematics and Applied Mathematics, Huaihua University, Huaihua, 418008 Hunan, P.R. China, e-mail: heyinprc@csu.edu.cn
Xianhua Tang*
Affiliation:
School of Mathematics and Statistics, Central South University, Changsha, 410083 Hunan, P.R.China, e-mail: qindd132@163.com Department of Mathematics and Applied Mathematics, Huaihua University, Huaihua, 418008 Hunan, P.R. China, e-mail: heyinprc@csu.edu.cn
*
tangxh@mail.csu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we consider the following critical Kirchhoff type equation:

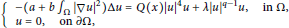$$\left\{ _{u\,=\,0,\,\,\,\,\,\,\text{on}\,\partial \Omega \text{,}}^{-(a\,+\,b{{\int }_{\Omega }}|\nabla u{{|}^{2}})\Delta u\,=\,\text{Q(}x)|u{{|}^{4}}u\,+\,\lambda |u{{|}^{q-1}}u,\,\,\,\text{in}\,\Omega \text{,}} \right.$$

By using variational methods that are constrained to the Nehari manifold, we prove that the above equation has a ground state solution for the case when 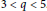$3\,<\,q\,<\,5$. The relation between the number of maxima of 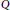$\text{Q}$ and the number of positive solutions for the problem is also investigated.

Keywords

35J2035J6035J25Kirchhoff type equationvariational methodscritical exponentNehari manifoldground state
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 2 , 01 June 2018 , pp. 353 - 369
Copyright
Copyright © Canadian Mathematical Society 2018

Footnotes

This work is partially supported by the China Scholarship Council, NSFC (Nos: 11626202, 11571370, 11471278, 11601525) and the Hunan Provincial Innovation Foundation for Postgraduates (CX2015B037).

References

[1] Al-Gwaiz, M., Benci, V., and Gazzola, F., Bending and stretching energies in a rectangular plate modeling Suspension bridges. Nonlinear Anal. 106(2014), 18–34.http://dx.doi.Org/10.1016/j.na.2014.04.011 Google Scholar
[2] Alves, C. O., Correa, F. J. S. A., and Figueiredo, G. M., On a class ofnonlocal elliptic problems with critical growth. Differ. Equ. Appl. 2(2010), 409–417.http://dx.doi.Org/10.7153/dea-02-25 Google Scholar
[3] Alves, C. O., Correa, F. J. S. A., and Ma, T. F., Positive Solutions for a quasilinear elliptic equation of Kirchhoff type. Comput. Math. Appl. 49(2005), 85–93.http://dx.doi.Org/10.1016/j.camwa.2005.01.008 Google Scholar
[4] Ambrosetti, A., Brezis, H., and Cerami, G., Combined effects ofconcave and convex nonlinearities in some elliptic problems. J. Funct. Anal. 122(1994), 519–543.http://dx.doi.Org/10.1006/jfan.1994.1078 Google Scholar
[5] Arosio, A. and Panizzi, S., On the well-posedness ofthe Kirchhoff string. Trans. Amer. Math. Soc. 348(1996), 305–330.http://dx.doi.org/10.1090/S0002-9947-96-01532-2 Google Scholar
[6] Benci, V. and Cerami, G., Positive Solutions of some nonlinear elliptic equations in exterior domains. Arch. Rational Mech. Anal. 99(1987), 283–300.http://dx.doi.org/10.1007/BF00282048 Google Scholar
[7] Brezis, H. and Nirenberg, L., Positive Solutions of nonlinear elliptic equations involving critical exponents. Commun. Pure Appl. Math. 36(1983), 437–477.http://dx.doi.org/10.1002/cpa.3160360405 Google Scholar
[8] Cao, D. M. and Chabrowski, J., Multiple Solutions of nonhomogeneous elliptic equation with critical nonlinearity. Differ. Integral Equ. 10(1997), 797–814.Google Scholar
[9] Cao, D. M., Peng, S. J., and Yan, S. S., Infinitely many Solutions for p-Laplacian equation involving critical Sobolev growth. J. Funct. Anal. 262(2012), 2861–2902. http://dx.doi.Org/10.1016/j.jfa.2O12.01.006 Google Scholar
[10] Chen, C.-Y., Kuo, Y.-C., and Wu, T.-F., The Nehari manifold for a Kirchhoff type problem involving sign-changing weight functions. J. Differential Equations 250(2011), 1876–1908. http://dx.doi.Org/10.1016/j.jde.2O10.11.017 Google Scholar
[11] Correa, F. J. S. A., On positive Solutions ofnonlocal and nonvariational elliptic problems. Nonlinear Anal. 59(2004), 1147–1155. http://dx.doi.Org/10.1016/j.na.2004.08.010 Google Scholar
[12] Devillanova, G. and Solimini, S., Concentration estimates and multiple Solutions to elliptic problems at critical growth. Adv. Differential Equations 7(2002), 1257–1280.Google Scholar
[13] Figueiredo, G. M., Existence ofa positive solution for a Kirchhoff problem type with critical growth via truncation argument. J. Math. Anal. Appl. 401(2013), 706–713. http://dx.doi.Org/10.1016/j.jmaa.2012.12.053 Google Scholar
[14] Hamydy, A., Massar, M., and Tsouli, N., Existence of solution for p-Kirchhoff type problems with critical exponents. Electron. J. Differential Equations 105(2011) 1–8.Google Scholar
[15] He, X. M. and Zou, W. M., Multiplicity of solutions for a class of Kirchhoff type problems. Acta Math. Appl. Sinica 26(2010), 387–394. http://dx.doi.org/10.1007/s10255-010-0005-2Google Scholar
[16] He, X. M. and Zou, W. M., Infinitely many positive solutions for Kirchhoff-type problem. Nonlinear Anal. 70(2009), 1407–1414. http://dx.doi.org/10.1016/j.na.2008.02.021Google Scholar
[17] He, Y. and Li, G. B., Standing waves for a class of Kirchhoff type problems in Rh involving critical Sobolev exponents. Calc. Var. 54(2015), 3067–3106. http://dx.doi.org/10.1007/s00526-015-0894-2Google Scholar
[18] Kirchhoff, G., Mechanik. Teubner, Leipzig, 1883.Google Scholar
[19] Lei, C. Y., Liu, G. S., and Guo, L. T., Multiple positive solutions for a Kirchhoff type problem with a critical nonlinearity. Nonlinear Anal. RealWorld Appl. 31(2016), 343–355. http://dx.doi.org/10.1016/j.nonrwa.2016.01.018Google Scholar
[20] Li, G. B. and Ye, H. Y., Existence of positive ground state solutions for the nonlinear Kirchhoff type problems in Rh. J. Differential Equations 257(2014), 566–600. http://dx.doi.org/10.1016/j.jde.2014.04.011Google Scholar
[21] Liao, J. F., Liu, J., Zhang, P., and Tang, C. L., Existence and multiplicity of positive solutions for a class of elliptic equations involving critical Sobolev exponents. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Math. RACSAM 110(2016), 483–501. http://dx.doi.org/10.1007/s13398-015-0244-4Google Scholar
[22] Lin, H. L., Positive solutions for nonhomogeneous elliptic equations involving critical Sobolev exponent. Nonlinear Anal. 75(2012), 2660–2671. http://dx.doi.org/10.1016/j.na.2011.11.008Google Scholar
[23] Lions, J. L., On some questions in boundary value problems of mathematical physics. In: Contemporary developments in continuum mechanics and partial diòerential equations. North-Holland Math. Stud., h§. North-Holland, Amsterdam, 1978, pp. 284-346.Google Scholar
[24] Lions, P. L., The concentration-compactness principle in the calculus of variations. The limit case, I. Rev. Mat. Iberoam. 1(1985), 145–201. http://dx.doi.org/10.4171/RMI/6Google Scholar
[25] Liu, Z. S. and Guo, S. J., On ground states for the Kirchhoff-type problem with a general critical nonlinearity. J. Math. Anal. Appl. 426(2015), 267–287. http://dx.doi.org/10.1016/j.jmaa.2015.01.044Google Scholar
[26] Mao, A. M. and Zhang, Z. T., Sign-changing and multiple solutions of Kirchhoff type problems without the P.S. condition. Nonlinear Anal. 70(2009), 1275–1287. http://dx.doi.org/10.1016/j.na.2008.02.011Google Scholar
[27] Perera, K. and Zhang, Z. T., Nontrivial solutions of Kirchhoff-type problems via the Yang index. J. Differential Equations 221(2006), 246–255. http://dx.doi.org/10.1016/j.jde.2005.03.006Google Scholar
[28] Qin, D. D., He, Y. B., and Tang, X. H., Ground state solutions for Kirchhoff type equations with asymptotically -linear nonlinearity. Comput. Math. Appl. 71(2016), 1524–1536. http://dx.doi.org/10.1016/j.camwa.2016.02.037Google Scholar
[29] Qin, D. D., Liao, F. F., He, Y. B., and Tang, X. H., Inûnitely many sign-changing solutions for Kirchhoff type equations in Rh. Bull. Malays. Math. Sci. Soc. (2017). http://dx.doi.org/10.1007/s40840-017-0534-4Google Scholar
[30] Rabinowitz, P. H., On a class of nonlinear Schrödinger equations. Z. Angew. Math. Phys. 43(1992), 270–291. http://dx.doi.org/10.1007/BF00946631Google Scholar
[31] Shuai, W., Sign-changing solutions for a class of Kirchhoff-type problem in bounded domains. J. Differential Equations 259(2015), 1256–1274. http://dx.doi.org/10.1016/j.jde.2015.02.040Google Scholar
[32] Tang, X. H., Non-Nehari manifold method for superlinear Schrödinger equation. Taiwanese J. Math. 18(2014). 1957-1979. http://dx.doi.org/10.11650/tjm.18.2014.3541Google Scholar
[33] Tang, X. H. and Chen, S. T., Ground state solutions of Nehari-Pohozaev type for Kirchhoff-type problems with general potentials. Calc. Var. Partial Differential Equations 56(2017), no. 4,56:110. http://dx.doi.org/10.1007/s00526-017-1214-9Google Scholar
[34] Tang, X. H. and Cheng, B. T., Ground state sign-changing solutions for Kirchhoff type problems in bounded domains. J. Differential Equations 261(2016), 2384–2402. http://dx.doi.org/10.1016/j.jde.2016.04.032Google Scholar
[35] Tarantello, G., On nonhomogeneous elliptic equations involving critical Sobolev exponent. Ann. Inst. H. Poincare Anal. Non Lineaire 9(1992), 281–304. http://dx.doi.org/10.1016/S0294-1449(16)30238-4Google Scholar
[36] Xie, Q. L., Wu, X. P., and Tang, C. L., Existence and multiplicity of solutions for Kirchhoff type problem with critical exponent. Commun. Pure Appl. Anal. 12(2013), 2773–2786. http://dx.doi.org/10.3934/cpaa.2013.12.2773Google Scholar
[37] Wang, J., Tian, L. X., Xu, J. X., and Zhang, F. B., Multiplicity and concentration of positive solutions for a Kirchhoff type problem with critical growth. J. Differential Equations 253(2012), 2314–2351. http://dx.doi.org/10.1016/j.jde.2012.05.023Google Scholar
[38] Willem, M., Minimax theorems. Progress in Nonlinear Differential Equations and their Applications, z. Birkhäuser Boston, Boston, 1996. http://dx.doi.org/10.1007/978-1-4612-4146-1Google Scholar
[39] Wu, T. F., On semilinear elliptic equations involving concave-convex nonlinearities and sign-changing weight function. J. Math. Anal. Appl. 318(2006), 253–270. http://dx.doi.org/10.1016/j.jmaa.2005.05.057Google Scholar
[40] Zhang, Z. and Perera, K., Sign changing solutions of Kirchhoff type problems via invariant sets of descent Thow,. J. Math. Anal. Appl. 317(2006), 456–463. http://dx.doi.org/10.1016/j.jmaa.2005.06.102Google Scholar