Hostname: page-component-84b7d79bbc-fnpn6 Total loading time: 0 Render date: 2024-07-29T12:47:11.715Z Has data issue: false hasContentIssue false
  • English
  • Français

Admissible Sequences for Twisted Involutions in Weyl Groups

Published online by Cambridge University Press:  20 November 2018

Ruth Haas  and
Aloysius G. Helminck
Ruth Haas
Affiliation:
Department of Mathematics, Smith College, Northampton, MA 01063, USAe-mail: rhaas@math.smith.edu
Aloysius G. Helminck
Affiliation:
Department of Mathematics, North Carolina State University, Raleigh, NC 27695-8205, USAe-mail: loek@unity.ncsu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

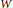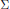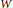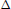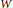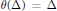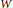Let $W$ be a Weyl group, $\sum $ a set of simple reflections in $W$ related to a basis $\Delta $ for the root system $\Phi $ associated with $W$ and $\theta $ an involution such that $\theta (\Delta )\,=\,\Delta $. We show that the set of $\theta $- twisted involutions in $W$, 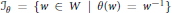${{\mathcal{J}}_{\theta }}\,=\,\{w\,\in \,W\,|\,\theta (w)\,=\,{{w}^{-1}}\}$ is in one to one correspondence with the set of regular involutions 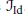${{\mathcal{J}}_{\text{ID}}}$. The elements of ${{\mathcal{J}}_{\theta }}$ are characterized by sequences in 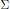$\sum $ which induce an ordering called the Richardson–Springer Poset. 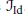In particular, for $\Phi $ irreducible, the ascending Richardson–Springer Poset of ${{\mathcal{J}}_{\theta }}$, for nontrivial $\theta $ is identical to the descending Richardson–Springer Poset of ${{\mathcal{J}}_{\text{ID}}}$.

Keywords

20G1520G2022E1522E4643A85
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 4 , 01 December 2011 , pp. 663 - 675
Copyright
Copyright © Canadian Mathematical Society 2011

References

[Bou81] Bourbaki, N., Groupes et algébres de Lie. Éléments de Mathématique, ch. Chapitres 4, 5 et 6, Masson, Paris, 1981.Google Scholar
[CHH+10] Cahn, P., Haas, R., Helminck, A. G., Li, J. and Schwartz, J., A data structure for the exceptional Weyl groups of type F 4 and G 2. In preparation.Google Scholar
[CHHW10] Cooley, C., Haas, R., Helminck, A. G. and Williams, N., Combinatorial properties of the Richardson-Springer involution poset. In preparation.Google Scholar
[HH010] Haas, R. and Helminck, A. G., Algorithms for twisted involutions in Weyl groups. Proceedings of the International Conference on Algebraic Groups and Related Topics, Algebraic Colloquium, Peking University, 2010, to appear.Google Scholar
[Hel88] Helminck, A. G., Algebraic groups with a commuting pair of involutions and semisimple symmetric spaces. Adv. in Math. 71(1988), 21–91. doi:10.1016/0001-8708(88)90066-7Google Scholar
[Hel91] Helminck, A. G., Tori invariant under an involutorial automorphism I. Adv. in Math. 85(1991), 1–38. doi:10.1016/0001-8708(91)90048-CGoogle Scholar
[Hel97] Helminck, A. G., Tori invariant under an involutorial automorphism II. Adv. in Math. 131(1997), 1–92. doi:10.1006/aima.1997.1633Google Scholar
[Hel00] Helminck, A. G., Computing orbits of minimal parabolic k-subgroups acting on symmetric k-varieties. J. Symbolic Comput. 30(2000), 521–553. doi:10.1006/jsco.2000.0395Google Scholar
[Hel04] Helminck, A. G., Combinatorics related to orbit closures of symmetric subgroups in flag varieties. CRM Proc. Lecture Notes 35(2004), 71–90.Google Scholar
[Hul05] Hultman, A., Fixed points of involutive automorphisms of the Bruhat order. Adv. Math. 195(2005), 283–296. doi:10.1016/j.aim.2004.08.011Google Scholar
[HW93] Helminck, A. G. and Wang, S. P., On rationality properties of involutions of reductive groups. Adv. in Math. 99(1993), 26–96. doi:10.1006/aima.1993.1019Google Scholar
[Inc04] Incitti, F., The Bruhat order on the involutions of the symmetric group. J. Algebraic Combin. 20(2004), 243–261. doi:10.1023/B:JACO.0000048514.62391.f4Google Scholar
[Inc06] Incitti, F., Bruhat order on the involutions of classical Weyl groups. Adv. in Appl. Math. 37(2006), 68–111. doi:10.1016/j.aam.2005.11.002Google Scholar
[Mat79] Matsuki, T., The orbits of affine symmetric spaces under the action of minimal parabolic subgroups. J. Math. Soc. Japan 31(1979), 331–357. doi:10.2969/jmsj/03120331Google Scholar
[Ros79] Rossmann, W., The structure of semisimple symmetric spaces. Canad. J. Math. 31(1979), 157–180.Google Scholar
[RS90] Richardson, R. W. and Springer, T. A., The Bruhat order on symmetric varieties. Geom. Dedicata 35(1990), 389–436.Google Scholar
[Spr85] Springer, T. A., Some results on algebraic groups with involutions. In: Algebraic groups and related topics (Kyoto/Nagoya, 1983), North-Holland, Amsterdam, 1985, 525–543.Google Scholar
[Ste68] Steinberg, R., Endomorphisms of linear algebraic groups. Mem. Amer. Math. Soc. 80, Amer. Math. Soc., Providence, RI, 1968.Google Scholar
[Vog83] Vogan, D. A., Irreducible characters of semi-simple Lie groups III. Proof of the Kazhdan–Lusztig conjectures in the integral case. Invent. Math. 71(1983), 381–417. doi:10.1007/BF01389104Google Scholar