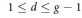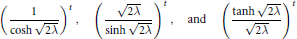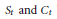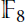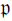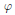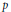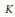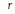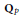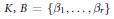Research Article
Short Kloosterman Sums for Polynomials over Finite Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-246
-
- Article
-
- You have access
- Export citation
Correction
Differential Structure of Orbit Spaces: Erratum
-
- Published online by Cambridge University Press:
- 20 November 2018, p. 247
-
- Article
-
- You have access
- Export citation
Research Article
A Generalized Torelli Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 248-265
-
- Article
-
- You have access
- Export citation
Two Algorithms for a Moving Frame Construction
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 266-291
-
- Article
-
- You have access
- Export citation
Infinitely Divisible Laws Associated with Hyperbolic Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 292-330
-
- Article
-
- You have access
- Export citation
The Maximum Number of Points on a Curve of Genus 4 over
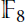 ${{\mathbb{F}}_{8}}$ is 25
${{\mathbb{F}}_{8}}$ is 25
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 331-352
-
- Article
-
- You have access
- Export citation
Weak Explicit Matching for Level Zero Discrete Series of Unit Groups of
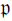 $\mathfrak{p}$-Adic Simple Algebras
$\mathfrak{p}$-Adic Simple Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 353-378
-
- Article
-
- You have access
- Export citation
Generalized Factorization in Hardy Spaces and the Commutant of Toeplitz Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 379-400
-
- Article
-
- You have access
- Export citation
Gaussian Estimates in Lipschitz Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 401-431
-
- Article
-
- You have access
- Export citation
Pair Correlation of Squares in
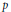 $p$-Adic Fields
$p$-Adic Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 432-448
-
- Article
-
- You have access
- Export citation