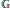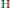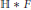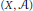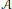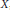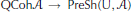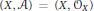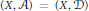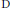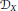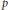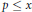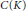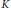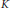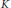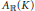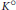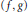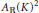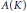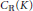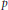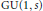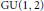We describe a noncommutative deformation theory for presheaves and sheaves of modules that generalizes the commutative deformation theory of these global algebraic structures and the noncommutative deformation theory of modules over algebras due to Laudal.
In the first part of the paper, we describe a noncommutative deformation functor for presheaves of modules on a small category and an obstruction theory for this functor in terms of global Hochschild cohomology. An important feature of this obstruction theory is that it can be computed in concrete terms in many interesting cases.
In the last part of the paper, we describe a noncommutative deformation functor for quasi-coherent sheaves of modules on a ringed space 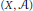 $\left( X,\,\mathcal{A} \right)$. We show that for any good
$\left( X,\,\mathcal{A} \right)$. We show that for any good 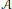 $\mathcal{A}$-affine open cover
$\mathcal{A}$-affine open cover  $\cup$ of
$\cup$ of 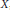 $X$, the forgetful functor
$X$, the forgetful functor 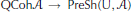 $\text{QCoh}\mathcal{A}\,\to \,\text{PreSh}\left( \cup ,\,\mathcal{A} \right)$ induces an isomorphism of noncommutative deformation functors.
$\text{QCoh}\mathcal{A}\,\to \,\text{PreSh}\left( \cup ,\,\mathcal{A} \right)$ induces an isomorphism of noncommutative deformation functors.
Applications. We consider noncommutative deformations of quasi-coherent 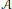 $\mathcal{A}$-modules on
$\mathcal{A}$-modules on 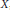 $X$ when
$X$ when 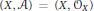 $\left( X,\,\mathcal{A} \right)\,=\,\left( X,\,{{\mathcal{O}}_{X}} \right)$ is a scheme or
$\left( X,\,\mathcal{A} \right)\,=\,\left( X,\,{{\mathcal{O}}_{X}} \right)$ is a scheme or 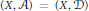 $\left( X,\,\mathcal{A} \right)\,=\,\left( X,\,\mathcal{D} \right)$ is a
$\left( X,\,\mathcal{A} \right)\,=\,\left( X,\,\mathcal{D} \right)$ is a  $\text{D}$-scheme in the sense of Beilinson and Bernstein. In these cases, we may use any open affine cover of
$\text{D}$-scheme in the sense of Beilinson and Bernstein. In these cases, we may use any open affine cover of  $X$ closed under finite intersections to compute noncommutative deformations in concrete terms using presheaf methods. We compute the noncommutative deformations of the left
$X$ closed under finite intersections to compute noncommutative deformations in concrete terms using presheaf methods. We compute the noncommutative deformations of the left 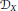 ${{\mathcal{D}}_{X}}$-module
${{\mathcal{D}}_{X}}$-module 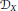 ${{\mathcal{D}}_{X}}$ when
${{\mathcal{D}}_{X}}$ when 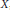 $X$ is an elliptic curve as an example.
$X$ is an elliptic curve as an example.