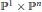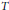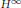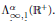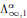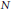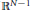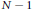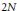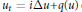Research Article
About the Defectivity of Certain Segre–Veronese Varieties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-974
-
- Article
-
- You have access
- Export citation
An AF Algebra Associated with the Farey Tessellation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 975-1000
-
- Article
-
- You have access
- Export citation
Isometric Group Actions on Hilbert Spaces: Structure of Orbits
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1001-1009
-
- Article
-
- You have access
- Export citation
H∞ Functional Calculus and Mikhlin-Type Multiplier Conditions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1010-1027
-
- Article
-
- You have access
- Export citation
Lifting n-Dimensional Galois Representations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1028-1049
-
- Article
-
- You have access
- Export citation
Adjacency Preserving Maps on Hermitian Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1050-1066
-
- Article
-
- You have access
- Export citation
On Types for Unramified p-Adic Unitary Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1067-1107
-
- Article
-
- You have access
- Export citation
A Classification of Tsirelson Type Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1108-1148
-
- Article
-
- You have access
- Export citation
Conjugate Reciprocal Polynomials with All Roots on the Unit Circle
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1149-1167
-
- Article
-
- You have access
- Export citation
Short Time Behavior of Solutions to Linear and Nonlinear Schrödinger Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1168-1200
-
- Article
-
- You have access
- Export citation