Article contents
Short Time Behavior of Solutions to Linear and Nonlinear Schrödinger Equations
Published online by Cambridge University Press: 20 November 2018
Abstract
We examine the fine structure of the short time behavior of solutions to various linear and nonlinear Schrödinger equations 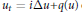 ${{u}_{t}}=i\Delta u+q(u)$ on
${{u}_{t}}=i\Delta u+q(u)$ on 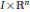 $I\times {{\mathbb{R}}^{n}}$, with initial data
$I\times {{\mathbb{R}}^{n}}$, with initial data  $u(0,x)=f(x)$. Particular attention is paid to cases where
$u(0,x)=f(x)$. Particular attention is paid to cases where 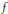 $f$ is piecewise smooth, with jump across an
$f$ is piecewise smooth, with jump across an 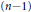 $(n-1)$-dimensional surface. We give detailed analyses of Gibbs-like phenomena and also focusing effects, including analogues of the Pinsky phenomenon. We give results for general
$(n-1)$-dimensional surface. We give detailed analyses of Gibbs-like phenomena and also focusing effects, including analogues of the Pinsky phenomenon. We give results for general  $n$ in the linear case. We also have detailed analyses for a broad class of nonlinear equations when
$n$ in the linear case. We also have detailed analyses for a broad class of nonlinear equations when 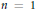 $n=1$ and 2, with emphasis on the analysis of the first order correction to the solution of the corresponding linear equation. This work complements estimates on the error in this approximation.
$n=1$ and 2, with emphasis on the analysis of the first order correction to the solution of the corresponding linear equation. This work complements estimates on the error in this approximation.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2008
References
- 1
- Cited by




