Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-07-02T13:08:48.053Z Has data issue: false hasContentIssue false
  • English
  • Français

Two Results Concerning the Zeros of Functions with Finite Dirichlet Integral

Published online by Cambridge University Press:  20 November 2018

James G. Caughran
James G. Caughran*
Affiliation:
University of Kentucky, Lexington, Kentucky
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A function f, analytic in the unit disk, is said to have finite Dirichlet integral if

1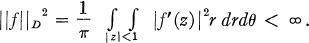

Geometrically, this is equivalent to f mapping the disk onto a Riemann surface of finite area. The class of Dirichlet integrable functions will be denoted by . The condition above can be restated in terms of Taylor coefficients; if f(z) = Σanzn, then 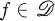if and only if Σn|an|2 < ∞. Thus, is contained in the Hardy class H2.

In particular, every such function has boundary values

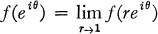
almost everywhere and log |f(eiθ)| ∊ L1(dθ).

The zeros zn of a function must satisfy the Blaschke condition

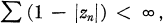
and f(s) = B(z)F(z), where F(z) has no zeros and

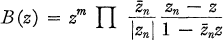
is the Blaschke product with zeros zn; see (5).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 312 - 316
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Beurling, Arne, Ensembles exceptionnels, Acta Math. 70 (1940), 1–13.Google Scholar
2. Carleson, Lennart, Sets of uniqueness for functions regular in the unit circle, i\cta Math. 87 (1952), 325–345.Google Scholar
3. Carleson, Lennart, On the zeros of functions with bounded Dirichlet integrals, Math. Z. 56 (1952), 289–295.Google Scholar
4. Carleson, Lennart, A representation theorem for the Dirichlet integral, Math. Z. 73 (1960), 190–196.Google Scholar
5. Hoffman, Kenneth, Banach spaces of analytic functions (Prentice-Hall, Englewood Cliffs, N.J., 1962).Google Scholar
6. Shapiro, H. S. and Shields, A. L., On the zeros of functions with finite Dirichlet integral and some related function spaces, Math. Z. 80 (1962), 217–229.Google Scholar