Hostname: page-component-7479d7b7d-jwnkl Total loading time: 0 Render date: 2024-07-12T08:37:45.316Z Has data issue: false hasContentIssue false
  • English
  • Français

A Summation Formula Involving σk(n), k > 1

Published online by Cambridge University Press:  20 November 2018

C. Nasim
C. Nasim*
Affiliation:
University of Calgary, Calgary, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The existence of certain formulae analogous to Poisson's summation formula (9, pp. 60-64),

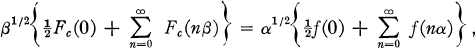
where αβ = 2π, α > 0, and Fc(x) is the Fourier cosine transform of f(x), but involving number-theoretic functions as coefficients, was first demonstrated by Voronoï (10) in 1904. He proved that

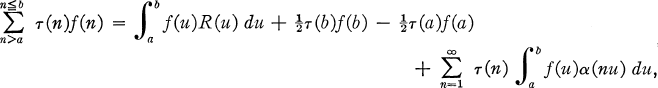
where r(n) is an arithmetic function,/(x) is continuous in (a, b) and a(x) and i?(x) are analytic functions dependent on τ(n). Later, numerous papers were published by various authors giving formulae of this type involving d(n), the number of divisors of n (3), and rp(n), the number of ways of expressing n as the sum of p squares of integers (8).

In 1937, Ferrar (4) developed a general theory of summation formulae, using complex analysis. Around that time, Guinand (5) also published papers where he developed the general theory from a different point of view. He applied the theory of mean convergence for the transforms of class L2(0, ∞ ). Later in 1950, Bochner (1) gave a general summation formula.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 951 - 964
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Bochner, S., Some properties of modular relations, Ann. of Math. (2) 53 (1951), 332–363.Google Scholar
2. Busbridge, I. W., A theory of general transforms of the class Lp(0, ∞) (1 <p ≦ 2), Quart. J. Math. Oxford Ser. 9 (1938), 148–160 Google Scholar
3. Dixon, A. L. and Ferrar, W. L., Lattice point summation formulae, Quart. J. Math. Oxford Ser. 2 (1931), 31–54.Google Scholar
4. Ferrar, W. L., Summation formulae and their relation to Dircichlet series. II, Compositio Math. 4 (1937), 394–405 Google Scholar
5. Guinand, A. P., Summation formulae and self-reciprocal functions. II, Quart. J. Math. Oxford Ser. 10 (38) (1939), 104–118.Google Scholar
6. Guinand, A. P., General transformations and the Parseval theorem, Quart. J. Math. Oxford Ser. 12 (45) (1941), 51–56.Google Scholar
7. Miller, J. B., A symmetrical convergence theory for general transforms, Proc. London Math. Soc. (3) 8 (1958), 224–241.Google Scholar
8. Oppenheim, A., Some identities in the theory of numbers, Proc. London Math. Soc. (2) 26 (1927), 295–350.Google Scholar
9. Titchmarsh, E. C., Introduction to the theory of Fourier integrals (Oxford Univ. Press, London, 1948).Google Scholar
10. Voronoï, G., Sur une fonction transcendante et ses applications à la sommation de quelques séries. I and II, Ann. Sci. École Norm. Sup. (3) 21 (1904), 207-268, 459–534.Google Scholar
11. Wilton, J. R., An extended form of Dirichlet divisor problem, Proc. London Math. Soc. (2) 36 (1933), 391–426.Google Scholar