Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kokhanovskii, A. P.
1975.
Tauberian theorems for semicontinuous logarithmic methods of summation of series.
Ukrainian Mathematical Journal,
Vol. 26,
Issue. 6,
p.
607.
Kokhanovskii, A. P.
1975.
The (l)-property of the semicontinuous logarithmic method of summation of series and Tauberian theorems.
Ukrainian Mathematical Journal,
Vol. 26,
Issue. 5,
p.
493.
Kangro, G. F.
1976.
Theory of summability of sequences and series.
Journal of Soviet Mathematics,
Vol. 5,
Issue. 1,
p.
1.
Parameswaran, Mangalam R.
1994.
New Tauberian Theorems from Old.
Canadian Journal of Mathematics,
Vol. 46,
Issue. 2,
p.
380.
Bingham, N.H.
and
Gashi, Bujar
2015.
Logarithmic moving averages.
Journal of Mathematical Analysis and Applications,
Vol. 421,
Issue. 2,
p.
1790.
Sezer, Sefa Anıl
and
Çanak, İbrahim
2018.
Tauberian Theorems for the Summability Methods of Logarithmic Type.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 41,
Issue. 4,
p.
1977.
Sezer, Sefa Anıl
and
Çanak, ˙Ibrahim
2019.
Theorems on the subsequential convergence.
Vol. 2091,
Issue. ,
p.
030042.
Sezer, S.A.
and
Çanak, İ.
2019.
On subsequentially convergent sequences.
Communications Faculty Of Science University of Ankara Series A1Mathematics and Statistics,
Vol. 68,
Issue. 2,
p.
1473.
Sezer, Sefa Anıl
and
Çanak, İbrahim
2020.
Tauberian Conditions of Slowly Decreasing Type for the Logarithmic Power Series Method.
Proceedings of the National Academy of Sciences, India Section A: Physical Sciences,
Vol. 90,
Issue. 1,
p.
135.
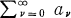 is said to be summable (L) to s if the sequence {sn}, where sn = a0 + a1 + … + an, is L-convergent to s, i.e., if
is said to be summable (L) to s if the sequence {sn}, where sn = a0 + a1 + … + an, is L-convergent to s, i.e., if