Hostname: page-component-5c6d5d7d68-wpx84 Total loading time: 0 Render date: 2024-08-15T19:17:17.483Z Has data issue: false hasContentIssue false
  • English
  • Français

Prime Dual Ideals in Boolean Algebras

Published online by Cambridge University Press:  20 November 2018

L. J. Heider
L. J. Heider*
Affiliation:
Institute for Advanced Study Marquette University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 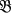denote an arbitrary Boolean algebra. Let Latin letters a, b, … denote general elements of 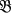while the symbols 0, 1 denote the special smallest and largest elements. Let Greek letters α, β, … denote various prime dual ideals of elements of 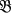. It is recalled that a prime dual ideal of 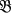is a proper subset of 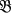closed under finite intersections of its elements and maximal with respect to those properties. Every prime dual ideal includes the element 1 and for each element a of 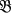includes either a or ā (complement of ain 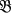) but not both. Occasional reference will be made to principal dual ideals of 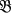. These are subsets of 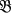composed of all elements of 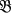majorizing some fixed non-zero element of 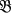. Finally, let X(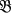) denote the collection of all prime dual ideals of .

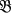Type
Research Article
Information
Canadian Journal of Mathematics , Volume 11 , 1959 , pp. 397 - 408
Copyright
Copyright © Canadian Mathematical Society 1959

References

1. Chang, C. C., On the representation of a-complete Boolean algebras, Trans. Amer. Math. Soc, 85 (1957), 208–18.Google Scholar
2. Enomoto, S., Boolean algebras and fields of sets, Osaka Math. J., 5 (1953), 99–115.Google Scholar
3. Gillman, L. and Henriksen, M., Concerning rings of continuous functions, Trans. Amer. Math. Soc, 77 (1954), 340-62.Google Scholar
4. Gillman, L. and Henriksen, M. Rings of continuous functions in which every finitely generated ideal is principal, Trans. Amer. Math. Soc, 82 (1956), 362-91.Google Scholar
5. Heider, L. J., A note concerning completely regular Gδ spaces, Proc Amer. Math. Soc, 8 (1957), 1060–6.Google Scholar
6. Heider, L. J., Compactifications of dimension zero, Notices Amer. Math. Soc, 552-9.Google Scholar
7. Hewitt, E., Rings of real-valued continuous functions, I, Trans. Amer. Math. Soc, 64 (1948), 45–99.Google Scholar
8. Isbell, J. R., Zero-dimensional spaces, Tohoku Math. J., 7 (1955), 1–8.Google Scholar
9. Pierce, R. S., Distributivity in Boolean algebras, Pacific J. Math., 7 (1957), 983–93.Google Scholar
10. Sikorski, R., On the representation of Boolean algebras as fields of sets, Fund. Math., 35 (1948), 247–58.Google Scholar
11. Smith, E. C. Jr.,, A distributivity condition for Boolean algebras, Ann. Math., 64 (1956), 551-61.Google Scholar
12. Stone, M. H., Boundedness properties in function lattices, Can. J. Math., 1 (1949), 176–86.Google Scholar