Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hill, Paul
1973.
New criteria for freeness in abelian groups.
Transactions of the American Mathematical Society,
Vol. 182,
Issue. 0,
p.
201.
Hill, Paul
1974.
New criteria for freeness in abelian groups. II.
Transactions of the American Mathematical Society,
Vol. 196,
Issue. 0,
p.
191.
Eklof, Paul C.
1975.
On the existence of 𝜅-free abelian groups.
Proceedings of the American Mathematical Society,
Vol. 47,
Issue. 1,
p.
65.
O’Neill, John D.
1977.
An uncountable Noetherian ring with free additive group.
Proceedings of the American Mathematical Society,
Vol. 66,
Issue. 2,
p.
205.
Mishina, A. P.
1982.
Abelian groups.
Journal of Soviet Mathematics,
Vol. 18,
Issue. 5,
p.
629.
1990.
Almost Free Modules - Set-theoretic Methods.
Vol. 46,
Issue. ,
p.
456.
Magidor, Menachem
and
Shelah, Saharon
1994.
When does almost free imply free? (For groups, transversals, etc.).
Journal of the American Mathematical Society,
Vol. 7,
Issue. 4,
p.
769.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
292.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
498.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
401.
Eklof, Paul C.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
85.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
55.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
316.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
441.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
143.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
264.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
527.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
17.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
476.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
563.
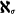 -free if each subgroup of rank less than
-free if each subgroup of rank less than 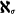 is free, these results are equivalent to: P is
is free, these results are equivalent to: P is 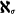 -free but not free.
-free but not free.



