Hostname: page-component-848d4c4894-sjtt6 Total loading time: 0 Render date: 2024-06-22T18:38:25.951Z Has data issue: false hasContentIssue false
  • English
  • Français

On Arithmetic Properties of the Taylor Series of Rational Functions

Published online by Cambridge University Press:  20 November 2018

David G. Cantor
David G. Cantor*
Affiliation:
University of California, Los Angeles, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Pólya (3) has shown that if bnis a sequence of algebraic integers and 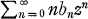is a rational function, then so is 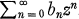. This result was generalized by Uchiyama (5) who showed that one may replace the assumption that the bn are algebraic integers by the assumption that the bn lie in a finitely generated submodule of the complex numbers, and by the author (1) who showed that if p is a non-zero polynomial with complex coefficients and if bn is a sequence of algebraic integers such that 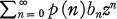is a rational function, then so is 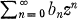. Our aim in this note is to give a common generalization of all of these theorems.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 378 - 382
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Cantor, D., On arithmetic properties of coefficients of rational functions, Pacific J. Math. 15 (1965), 55–58.Google Scholar
2. Lang, S., Introduction to algebraic geometry (Interscience, New York, 1958).Google Scholar
3. Pôlya, G., Arithmetische Eigenschaften der Reihenentwicklungen, J. Reine Angew. Math. 151 (1921), 1–31.Google Scholar
4. Salem, R., Algebraic numbers and Fourier analysis (D. C. Heath, Boston, Massachusetts, 1963).Google Scholar
5. Uchiyama, S., On a theorem of G. Pôlya, Proc. Japan Acad. 41 (1965), 517–520.Google Scholar