Hostname: page-component-5c6d5d7d68-thh2z Total loading time: 0 Render date: 2024-08-15T18:40:59.004Z Has data issue: false hasContentIssue false
  • English
  • Français

Moving Weighted Averages

Published online by Cambridge University Press:  20 November 2018

M. A. Akcoglu  and
Y. Déniel
M. A. Akcoglu
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario M5S 1A1
Y. Déniel
Affiliation:
Département de Mathématiques et Informatique, Université de Bretagne occidentale, 6, avenue Victor le Gorgeu, 29287 Brest, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ℝ denote the real line. Let {Tt}tєℝ be a measure preserving ergodic flow on a non atomic finite measure space (X, ℱ, μ). A nonnegative function φ on ℝ is called a weight function if ∫ℝ φ(t)dt = 1. Consider the weighted ergodic averages

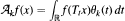
of a function f X —> ℝ, where {θk} is a sequence of weight functions. Some sufficient and some necessary and sufficient conditions are given for the a.e. convergence of Akf, in particular for a special case in which

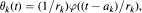
where φ is a fixed weight function and {(ak, rk)} is a sequence of pairs of real numbers such that rk > 0 for all k. These conditions are obtained by a combination of the methods of Bellow-Jones-Rosenblatt, developed to deal with moving ergodic averages, and the methods of Broise-Déniel-Derriennic, developed to deal with unbounded weight functions.

Keywords

28D9947A35maximal ergodic theoremsrearrangements
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 45 , Issue 3 , 01 June 1993 , pp. 449 - 469
Copyright
Copyright © Canadian Mathematical Society 1993

References

1. Bellow, A., Jones, R. and Rosenblatt, J., Convergence for moving averages, J.Erg. Th. Dyn. Sys. 10(1990), 43–62.Google Scholar
2. Bellow, A., Jones, R. and Rosenblatt, J., Almost everywhere convergence of weighted averages, preprint.Google Scholar
3. Bellow, A., Jones, R. and Rosenblatt, J., Almost everywhere convergence of powers, preprint.Google Scholar
4. Bellow, A. and Losert, V., The weighted pointwise ergodic theorem and the individual ergodic theorem along subsequences,Trans. Amer. Math. Soc. 288(1985), 349–353.Google Scholar
5. Broise, M., Déniel, Y. and Derriennic, Y., Réarrangement, inégalités maximales et théorèmes ergodiques fractionnaires, Ann. Inst. Fourier, Grenoble 39(1989), 689–714.Google Scholar
6. Broise, M., Déniel, Y. and Derriennic, Y., Maximal inequalities and ergodic theorems for Cesàro-a or weighted averages, preprint.Google Scholar
7. Calderon, A. P., Ergodic theory and translation invariant operators, Proc. Nat. Acad. Sci. 59(1968), 349–353.Google Scholar
8. Déniel, Y, On the a.e. Cesàro-a convergencefor stationary or orthogonal random variables, J. Theoretical Probability 2(1989), 475–485.Google Scholar
9. Déniel, Y and Derriennic, Y, Sur la convergence presque sûre au sens de Cesàro d'ordre α 0 < α < 1, de v.a. i.i.d., Prob. Th. 79(1988), 629–639.Google Scholar
10. Hardy, G. H., Littlewood, J. E. and Polya, G., Inequalities, Cambridge Univ. Press, 1934.Google Scholar
11. Jones, R. and Olsen, J., Subsequence ergodic theorems for operators, preprint.Google Scholar
12. Jones, R., Olsen, J. and Wierdl, M., Subsequence ergodic theorems for LP contractions, preprint.Google Scholar
13. Nagel, A. and Stein, E. M., On certain maximal functions and approach regions, Adv. Math. 54(1984), 83–106.Google Scholar
14. Rosenblatt, J. and Wierdl, M., A new maximal inequality and applications, preprint.Google Scholar
15. Sueiro, J., A note on maximal operators of’ Hardy-Little wood type, Math. Proc. Camb. Phil. Soc. 102(1987), 131–134.Google Scholar
16. Zygmund, A., Trigonometric Series, Cambridge Univ. Press, 1968 Google Scholar