Hostname: page-component-848d4c4894-xfwgj Total loading time: 0 Render date: 2024-06-27T18:01:08.012Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal Operators for Schrodinger-Type Differential Expressions with Discontinuous Principal Coefficients

Published online by Cambridge University Press:  20 November 2018

M. Faierman  and
I. Knowles
M. Faierman
Affiliation:
University of the Witwatersrand, Johannesburg, South Africa
I. Knowles
Affiliation:
University of the Witwatersrand, Johannesburg, South Africa
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The objective of this paper is to extend the recent results [7, 8, 9] concerning the self-adjointness of Schrödinger-type operators with singular potentials to a more general setting. We shall be concerned here with formally symmetric elliptic differential expressions of the form

1.1

where x = (x1, …, xm) ∈ Rm (and m ≧ 1), i = (–1)1/2, ∂j = ∂/∂xj, and the coefficients ajk, bj and q are real-valued and measurable on Rm.

The basic problem that we consider is that of deciding whether or not the formal operator 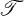defined by (1.1) determines a unique self-adjoint operator in the space L2(Rm) of (equivalence classes of) square integrable complex-valued functions on Rm.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 6 , 01 December 1980 , pp. 1423 - 1437
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Agmon, S., Lectures on elliptic boundary value problems, Math. Studies (Princeton, N.J., Van Nostrand, 1965).Google Scholar
2. Devinatz, A., Selfadjointness of second order elliptic and degenerate elliptic differential operators, Proceedings of the Uppsala 1977 International Conference on Differential Equations, Acta Universitatis Upsaliensis (Stockholm, Almqvist & Wiksell, 1977), 37–51.Google Scholar
3. Eastham, M. S. P., Evans, W. D. and McLeod, J. B., The essential self-adjointness of Schrodinger-type operators, Arch. Rational Mech. Anal. 60 (1976), 185–204.Google Scholar
4. Evans, W. D., On the essential self-adjointness of powers of Schrodinger-type operators, Proc. Royal Soc. Edinburgh Section A, 79 (1977), 61–77.Google Scholar
5. Kato, T., Perturbation theory for linear operators (Heidelberg, Springer, 1976).Google Scholar
6. Kato, T., Schrödinger operators with singular potentials, Israel J. Math. 13 (1972), 135–148.Google Scholar
7. Kato, T., A second look at the essential self-adjointness of the Schrodinger operator, Physical reality and mathematical description (Dordrecht, Reidel, 1974).Google Scholar
8. Knowles, I., On essential self-adjointness for singular elliptic differential operators, Math. Ann. 227 (1977), 155–172.Google Scholar
9. Knowles, I., On the existence of minimal operators for Schrodinger-type differential expressions, Math. Ann. 233 (1978), 221–227.Google Scholar
10. Ladyzhenskaya, O. A. and Ural'tseva, N. W., Linear and quasilinear elliptic equations (New York, Academic Press, 1968).Google Scholar
11. Naimark, M. A., Linear differential operators II (New York, Ungar, 1968).Google Scholar
12. Reed, M. and Simon, B., Methods of modern mathematical physics, Vol. II: Fourier analysis, self-adjointness (New York, London, Academic Press, 1972).Google Scholar