Let 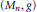$\left( {{M}_{n}},\,g \right)$ be a strictly convex riemannian manifold with 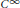${{C}^{\infty }}$ boundary. We prove the existence of classical solution for the nonlinear elliptic partial differential equation of Monge-Ampère: 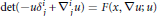$\det (-u\delta _{j}^{i}\,+\,\nabla _{j}^{i}u)\,=\,F(x,\,\nabla u;\,u)$ in 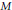$M$ with a Neumann condition on the boundary of the form 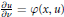$\frac{\partial u}{\partial v}=\varphi (x,u)$, where 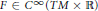$F\in {{C}^{\infty }}(TM\times \mathbb{R})$ is an everywhere strictly positive function satisfying some assumptions, $v$ stands for the unit normal vector field and 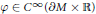$\varphi \in {{C}^{\infty }}(\partial M\times \mathbb{R})$ is a non-decreasing function in $u$.