Article contents
Aϕ-Invariant Subspaces on the Torus
Published online by Cambridge University Press: 20 November 2018
Abstract
Generalizing the notion of invariant subspaces on the 2-dimensional torus 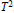 ${{T}^{2}}$, we study the structure of
${{T}^{2}}$, we study the structure of 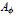 ${{A}_{\phi }}$-invariant subspaces of
${{A}_{\phi }}$-invariant subspaces of 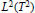 ${{L}^{2}}({{T}^{2}})$. A complete description is given of
${{L}^{2}}({{T}^{2}})$. A complete description is given of 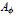 ${{A}_{\phi }}$-invariant subspaces that satisfy conditions similar to those studied by Mandrekar, Nakazi, and Takahashi.
${{A}_{\phi }}$-invariant subspaces that satisfy conditions similar to those studied by Mandrekar, Nakazi, and Takahashi.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1998
References
- 3
- Cited by


