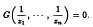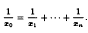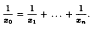Research Article
A generalised exchange theorem for matroid bases
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-180
-
- Article
-
- You have access
- Export citation
Variational and numerical methods for symmetric matrix pencils
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-17
-
- Article
-
- You have access
- Export citation
Signal spaces—an axiomatic approach to space-time
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 355-363
-
- Article
-
- You have access
- Export citation
On quasicaustics and their logarithmic vector fields
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 365-376
-
- Article
-
- You have access
- Export citation
A law of the iterated logarithm for martingales
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 181-185
-
- Article
-
- You have access
- Export citation
Highly transitive representations of free groups and free products
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 19-36
-
- Article
-
- You have access
- Export citation
The topological configuration of a real algebraic curve
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 37-50
-
- Article
-
- You have access
- Export citation
On quasi-monotone sequences and their applications
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 187-192
-
- Article
-
- You have access
- Export citation
Characterisation of drop and weak drop properties for closed bounded convex sets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 377-385
-
- Article
-
- You have access
- Export citation
Lefschetz numbers and unitary groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 193-209
-
- Article
-
- You have access
- Export citation
On time dependent multistep dynamic processes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 51-61
-
- Article
-
- You have access
- Export citation
Monochromatic solutions to equations with unit fractions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 387-392
-
- Article
-
- You have access
- Export citation
Volume inequalities using sections of convex sets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 393-397
-
- Article
-
- You have access
- Export citation
Existence of optimal controls for a class of nonlinear distributed parameter systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 211-224
-
- Article
-
- You have access
- Export citation
Nonsingular retractable modules and their endomorphism rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 63-71
-
- Article
-
- You have access
- Export citation
Some Banach space embeddings of classical function spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 73-77
-
- Article
-
- You have access
- Export citation
Hyperbolic flows are topologically stable
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 225-232
-
- Article
-
- You have access
- Export citation
On holomorphic differentials of some algebraic function field of one variable over C
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 399-405
-
- Article
-
- You have access
- Export citation
On an angle between two rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 79-87
-
- Article
-
- You have access
- Export citation
Topological dimensions of global attractors for semilinear PDE's with delays
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 407-422
-
- Article
-
- You have access
- Export citation



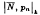 summability factors of infinite series, which generalises a theorem of Mazhar [7] on |
summability factors of infinite series, which generalises a theorem of Mazhar [7] on |