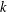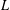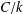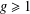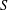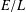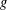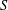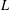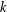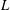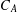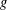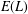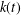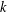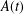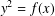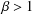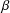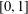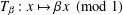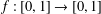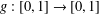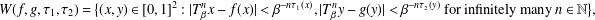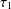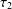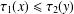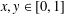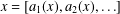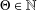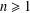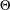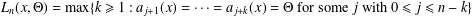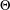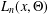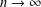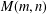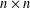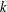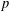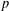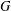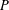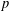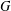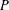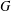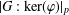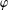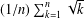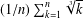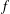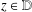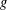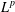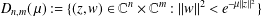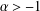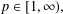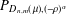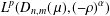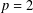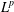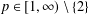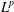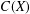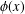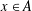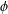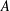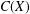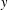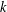Research Article
ON INTEGRAL POINTS ON ISOTRIVIAL ELLIPTIC CURVES OVER FUNCTION FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 27 March 2020, pp. 177-185
-
- Article
- Export citation
SIMULTANEOUS DYNAMICAL DIOPHANTINE APPROXIMATION IN BETA EXPANSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 186-195
-
- Article
- Export citation
ON THE LONGEST BLOCK FUNCTION IN CONTINUED FRACTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2020, pp. 196-206
-
- Article
- Export citation
ON SUMS OF TWO PRIME SQUARES, FOUR PRIME CUBES AND POWERS OF TWO
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 207-216
-
- Article
- Export citation
UNIFORM ASYMPTOTIC FORMULAS FOR RESTRICTED BIPARTITE PARTITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 05 February 2020, pp. 217-225
-
- Article
- Export citation
IRREDUCIBLE FAMILIES OF COMPLEX MATRICES CONTAINING A RANK-ONE MATRIX
- Part of:
-
- Published online by Cambridge University Press:
- 16 January 2020, pp. 226-236
-
- Article
- Export citation
DEGREES OF BRAUER CHARACTERS AND NORMAL SYLOW
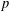 $p$-SUBGROUPS
$p$-SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 237-239
-
- Article
- Export citation
INEQUALITIES FOR DRAGOMIR’S MAPPINGS VIA STIELTJES INTEGRALS
- Part of:
-
- Published online by Cambridge University Press:
- 16 January 2020, pp. 240-250
-
- Article
- Export citation
ALGEBRAIC STRUCTURE OF THE RANGE OF A TRIGONOMETRIC POLYNOMIAL
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 251-260
-
- Article
- Export citation
THE FLOOR OF THE ARITHMETIC MEAN OF THE CUBE ROOTS OF THE FIRST
 $n$ INTEGERS
$n$ INTEGERS
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 261-267
-
- Article
- Export citation
ON A CLOSE-TO-CONVEX ANALOGUE OF CERTAIN STARLIKE FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2020, pp. 268-281
-
- Article
- Export citation
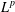 $L^{p}$ REGULARITY OF THE WEIGHTED BERGMAN PROJECTION ON THE FOCK–BARGMANN–HARTOGS DOMAIN
$L^{p}$ REGULARITY OF THE WEIGHTED BERGMAN PROJECTION ON THE FOCK–BARGMANN–HARTOGS DOMAIN
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 282-292
-
- Article
- Export citation
HYPERSTABILITY OF GENERALISED LINEAR FUNCTIONAL EQUATIONS IN SEVERAL VARIABLES
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 293-302
-
- Article
- Export citation
MULTIPLICATIVE SPECTRAL FUNCTIONALS ON
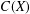 $C(X)$
$C(X)$
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 303-307
-
- Article
- Export citation
INEQUALITIES OF JENSEN’S TYPE FOR POSITIVE LINEAR FUNCTIONALS ON HERMITIAN UNITAL BANACH
 $\ast$-ALGEBRAS
$\ast$-ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 308-318
-
- Article
- Export citation
GRADIENT ESTIMATES VIA TWO-POINT FUNCTIONS FOR PARABOLIC EQUATIONS UNDER RICCI FLOW
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2020, pp. 319-330
-
- Article
- Export citation
ON THE PROBLEM OF NON-BERWALDIAN LANDSBERG SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 331-341
-
- Article
- Export citation
ON THE
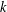 $k$-ERROR LINEAR COMPLEXITY OF SEQUENCES FROM FUNCTION FIELDS
$k$-ERROR LINEAR COMPLEXITY OF SEQUENCES FROM FUNCTION FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 342-352
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
BAZ volume 102 Issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 21 August 2020, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
BAZ volume 102 Issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 21 August 2020, pp. b1-b2
-
- Article
-
- You have access
- Export citation