Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-05-01T16:54:51.503Z Has data issue: false hasContentIssue false
  • English
  • Français

MULTIPLE SOLUTIONS FOR 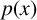$p(x)$-LAPLACIAN EQUATIONS WITH NONLINEARITY SUBLINEAR AT ZERO

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  29 January 2024

SHIBO LIU Open the ORCID record for SHIBO LIU [Opens in a new window]
SHIBO LIU*
Affiliation:
Department of Mathematics and Systems Engineering, Florida Institute of Technology, Melbourne 32901, FL, USA
*
e-mail: sliu@fit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the Dirichlet problem for 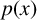$p(x)$-Laplacian equations of the form

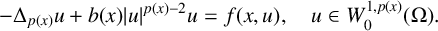$$ \begin{align*} -\Delta_{p(x)}u+b(x)\vert u\vert ^{p(x)-2}u=f(x,u),\quad u\in W_{0}^{1,p(x)}(\Omega). \end{align*} $$

The odd nonlinearity 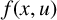$f(x,u)$ is 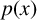$p(x)$-sublinear at 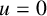$u=0$ but the related limit need not be uniform for 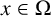$x\in \Omega $. Except being subcritical, no additional assumption is imposed on 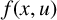$f(x,u)$ for 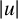$|u|$ large. By applying Clark’s theorem and a truncation method, we obtain a sequence of solutions with negative energy and approaching the zero function 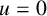$u=0$.

Keywords

p(x)-LaplacianClark’s theoremtruncation(PS)c condition

MSC classification

Primary: 35J60: Nonlinear elliptic equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 9
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chinnì, A., Sciammetta, A. and Tornatore, E., ‘Existence of non-zero solutions for a Dirichlet problem driven by $\left(p(x),q(x)\right)$ -Laplacian’, Appl. Anal. 101(15) (2022), 5323–5333.CrossRefGoogle Scholar
Diening, L., Harjulehto, P., Hästö, P. and Růžička, M., Lebesgue and Sobolev Spaces with Variable Exponents, Lecture Notes in Mathematics, 2017 (Springer, Heidelberg, 2011).CrossRefGoogle Scholar
Fan, X. and Zhang, Q., ‘Existence of solutions for $p(x)$ -Laplacian Dirichlet problem’, Nonlinear Anal. 52(8) (2003), 1843–1852.CrossRefGoogle Scholar
Fan, X. and Zhao, D., ‘On the spaces ${L}^{p(x)}(\Omega)$ and ${W}^{m,p(x)}(\Omega )$ ’, J. Math. Anal. Appl. 263(2) (2001), 424–446.CrossRefGoogle Scholar
He, W. and Wu, Q., ‘Multiplicity results for sublinear elliptic equations with sign-changing potential and general nonlinearity’, Bound. Value Probl. 2020 (2020), Article no. 159, 9 pages.CrossRefGoogle Scholar
Jikov, V. V., Kozlov, S. M. and Oleĭnik, O. A., Homogenization of Differential Operators and Integral Functionals (Springer-Verlag, Berlin, 1994). Translated from the Russian by G. A. Yosifian.CrossRefGoogle Scholar
Liang, S. and Zhang, J., ‘Infinitely many small solutions for the $p(x)$ -Laplacian operator with nonlinear boundary conditions’, Ann. Mat. Pura Appl. (4) 192(1) (2013), 1–16.CrossRefGoogle Scholar
Liu, Z. and Wang, Z.-Q., ‘On Clark’s theorem and its applications to partially sublinear problems’, Ann. Inst. H. Poincaré Anal. Non Linéaire 32(5) (2015), 1015–1037.CrossRefGoogle Scholar
Růžička, M., Electrorheological Fluids: Modeling and Mathematical Theory, Lecture Notes in Mathematics, 1748 (Springer-Verlag, Berlin, 2000).CrossRefGoogle Scholar
Taarabti, S., ‘Positive solutions for the $p(x)$ -Laplacian: application of the Nehari method’, Discrete Contin. Dyn. Syst. Ser. S 15(1) (2022), 229–243.CrossRefGoogle Scholar
Tavares, L. and Sousa, J. V. C., ‘Multiplicity results for a system involving the $p(x)$ -Laplacian operator’, Appl. Anal. 102(5) (2023), 1271–1280.CrossRefGoogle Scholar