Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pasteczka, P.
2015.
On negative results concerning Hardy means.
Acta Mathematica Hungarica,
Vol. 146,
Issue. 1,
p.
98.
Pasteczka, Paweł
2018.
Interval-type theorems concerning means.
Annales Universitatis Paedagogicae Cracoviensis. Studia Mathematica,
Vol. 17,
Issue. 1,
p.
37.
PASTECZKA, PAWEŁ
2020.
WEAKENING OF THE HARDY PROPERTY FOR MEANS.
Bulletin of the Australian Mathematical Society,
Vol. 101,
Issue. 1,
p.
118.
Pasteczka, Paweł
2022.
On the integral approach to means and their Hardy property.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 116,
Issue. 4,




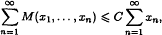 ,
Where
,
Where 