Hostname: page-component-848d4c4894-tn8tq Total loading time: 0 Render date: 2024-06-22T16:54:57.324Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterisations of Bloch functions in the unit ball of ℂn, I

Published online by Cambridge University Press:  17 April 2009

Zengjian Lou  and
Hasi Wulan
Zengjian Lou
Affiliation:
Department of Mathematics, Shantou University, Shantou Guangdong 515063, Peoples Republic of China, e-mail: zjlou@stu.edu.cn and Mathematical Sciences Institute, The Australian National University, Canberra ACT 0200, Australia
Hasi Wulan
Affiliation:
Department of Mathematics, Shantou University, Shantou Guangdong 515063, Peoples Republic of China, e-mail: wulan@stu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Weighted Hadamard product characterisations of Bloch functions in the unit ball of ℂn are studied. In particular, we prove that f belongs to the Bloch space ℬ(Bn) if and only if the non-weighted Hadamard products of f and g belong to BMOA(Un) for all f in 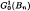, a subspace of the Hardy space H1(Bn).

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 68 , Issue 2 , October 2003 , pp. 205 - 212
Copyright
Copyright © Australian Mathematical Society 2003

References

[1]Anderson, J.M. and Shields, A.L., ‘Coefficient multipliers of Bloch functions’, Trans. Amer. Math. Soc. 224 (1976), 255–265.CrossRefGoogle Scholar
[2]Beatrous, F. and Burbea, J., ‘Holomorphic Sobolev spaces on the unit ball’, Dissertationes Math. 276 (1989), 1–57.Google Scholar
[3]Burbea, J. and Li, S., ‘Weighted Hadamard products of holomorphic functions in the unit ball’, Pacific J. Math. 168 (1995), 235–270.CrossRefGoogle Scholar
[4]Garnett, J.B., Bounded analytic functions (Academic Press, New York, 1981).Google Scholar
[5]Lou, Z., ‘Multipliers of Hp, Gp and Bloch spaces’, Math. Japon. 36 (1991), 21–26.Google Scholar
[6]Lou, Z., ‘Characterizations of Bloch functions on the unit ball of ℂn’, Kodai Math. J. 16 (1993), 74–78.CrossRefGoogle Scholar
[7]Lou, Z., ‘Carleson measure characterizations of Bloch functions’, Acta Math. Sinica 12 (1996), 175–184.Google Scholar
[8]Lou, Z., ‘Coefficient multipliers of Bergman spaces Ap, II’, Canad. Math. Bull. 40 (1997), 475–487.CrossRefGoogle Scholar
[9]Mateljevic, M. and Pavlovic, M., ‘Multipliers of Hp and BMOA’, Pacific J. Math. 146 (1990), 71–84.CrossRefGoogle Scholar
[10]Shi, J., ‘On the rate of growth of the means Mg of holomorphic and pluriharmonic functions on bounded symmetric domains of ℂn’, J. Math. Anal. Appl. 126 (1987), 161–175.CrossRefGoogle Scholar
[11]Timoney, R. M., ‘Bloch functions in several complex variables, I’, Bull. London Math. Soc. 12 (1980), 241–267.CrossRefGoogle Scholar