Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-26T12:48:56.611Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE DIVISIBILITY AMONG POWER LCM MATRICES ON GCD-CLOSED SETS

Part of: Special matrices Elementary number theory Polynomials and matrices

Published online by Cambridge University Press:  19 May 2022

GUANGYAN ZHU  and
MAO LI
GUANGYAN ZHU*
Affiliation:
Mathematical College, Sichuan University, Chengdu 610064, PR China and School of Teacher Education, Hubei Minzu University, Enshi 445000, PR China
MAO LI
Affiliation:
School of Mathematics and Statistics, Southwest University, Chongqing 400715, PR China e-mail: limao@swu.edu.cn
*
e-mail: 2009043@hbmzu.edu.cn, zhuguangyan45@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 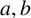$a,b$ and n be positive integers and let 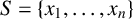$S=\{x_1, \ldots , x_n\}$ be a set of n distinct positive integers. For 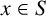${x\in S}$ , define 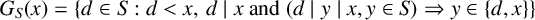$G_{S}(x)=\{d\in S: d<x, \,d\mid x \ \mathrm {and} \ (d\mid y\mid x, y\in S)\Rightarrow y\in \{d,x\}\}$ . Denote by 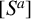$[S^a]$ the $n\times n$ matrix having the ath power of the least common multiple of 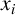$x_i$ and 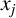$x_j$ as its 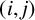$(i,j)$ -entry. 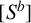We show that the bth power matrix $[S^b]$ is divisible by the ath power matrix 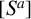$[S^a]$ if 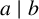$a\mid b$ and S is gcd closed (that is, 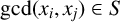$\gcd (x_i, x_j)\in S$ for all integers i and j with 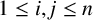$1\le i, j\le n$ ) and 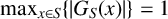$\max _{x\in S} \{|G_S (x)|\}=1$ . This confirms a conjecture of Shaofang Hong [‘Divisibility properties of power GCD matrices and power LCM matrices’, Linear Algebra Appl. 428 (2008), 1001–1008].

Keywords

divisibilitypower LCM matrixgcd-closed setgreatest-type divisor

MSC classification

Primary: 11C20: Matrices, determinants
Secondary: 11A05: Multiplicative structure; Euclidean algorithm; greatest common divisors 15B36: Matrices of integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 1 , February 2023 , pp. 31 - 39
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altinisik, E., Yildiz, M. and Keskin, A., ‘Non-divisibility of LCM matrices by GCD matrices on gcd-closed sets’, Linear Algebra Appl. 516 (2017), 47–68.CrossRefGoogle Scholar
Bege, A., ‘Generalized LCM matrices’, Publ. Math. Debrecen 79 (2011), 309–315.CrossRefGoogle Scholar
Beslin, S. and Ligh, S., ‘Another generalization of Smith’s determinant’, Bull. Aust. Math. Soc. 40 (1989), 413–415.CrossRefGoogle Scholar
Bourque, K. and Ligh, S., ‘On GCD and LCM matrices’, Linear Algebra Appl. 174 (1992), 65–74.CrossRefGoogle Scholar
Bourque, K. and Ligh, S., ‘Matrices associated with arithmetical functions’, Linear Multilinear Algebra 34 (1993), 261–267.CrossRefGoogle Scholar
Chen, L., Feng, Y. L., Hong, S. F. and Qiu, M., ‘On the divisibility of matrices associated with multiplicative functions’, Publ. Math. Debrecen 100 (2022), 323–335.CrossRefGoogle Scholar
Feng, W. D., Hong, S. F. and Zhao, J. R., ‘Divisibility properties of power LCM matrices by power GCD matrices on gcd-closed sets’, Discrete Math. 309 (2009), 2627–2639.CrossRefGoogle Scholar
Hong, S. A., Hu, S. N. and Lin, Z. B., ‘On a certain arithmetical determinant’, Acta Math. Hungar. 150 (2016), 372–382.CrossRefGoogle Scholar
Hong, S. F., ‘On the Bourque–Ligh conjecture of least common multiple matrices’, J. Algebra 218 (1999), 216–228.CrossRefGoogle Scholar
Hong, S. F., ‘On the factorization of LCM matrices on gcd-closed sets’, Linear Algebra Appl. 345 (2002), 225–233.CrossRefGoogle Scholar
Hong, S. F., ‘Notes on power LCM matrices’, Acta Arith. 111 (2004), 165–177.CrossRefGoogle Scholar
Hong, S. F., ‘Divisibility properties of power GCD matrices and power LCM matrices’, Linear Algebra Appl. 428 (2008), 1001–1008.CrossRefGoogle Scholar
Hong, S. F., Zhao, J. R. and Yin, Y. Z., ‘Divisibility properties of Smith matrices’, Acta Arith. 132 (2008), 161–175.CrossRefGoogle Scholar
Korkee, I. and Haukkanen, P., ‘On the divisibility of meet and join matrices’, Linear Algebra Appl. 429 (2008), 1929–1943.CrossRefGoogle Scholar
Smith, H. J. S., ‘On the value of a certain arithmetical determinant’, Proc. Lond. Math. Soc. (3) 7 (1875), 208–212.CrossRefGoogle Scholar
Tan, Q. R. and Li, M., ‘Divisibility among power GCD matrices and among power LCM matrices on finitely many coprime divisor chains’, Linear Algebra Appl. 438 (2013), 1454–1466.CrossRefGoogle Scholar
Zhao, J. R., ‘Divisibility of power LCM matrices by power GCD matrices on gcd-closed sets’, Linear Multilinear Algebra 62 (2014), 735–748.10.1080/03081087.2013.786717CrossRefGoogle Scholar
Zhao, J. R., Chen, L. and Hong, S. F., ‘Gcd-closed sets and divisibility of Smith matrices’, J. Combin. Theory Ser. A 188 (2022), Article no. 105581, 23 pages.CrossRefGoogle Scholar
Zhu, G. Y., ‘On the divisibility among power GCD and power LCM matrices on gcd-closed sets’, Int. J. Number Theory, to appear.Google Scholar
Zhu, G. Y., ‘On a certain determinant for a U.F.D.’, Colloq. Math., to appear.Google Scholar
Zhu, G. Y., Cheng, K. M. and Zhao, W., ‘Notes on Hong’s conjecture on nonsingularity of power LCM matrices’, AIMS Math. 7 (2022), 10276–10285.CrossRefGoogle Scholar