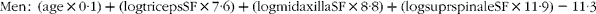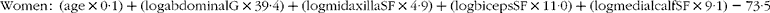Valid and reliable methods of measurement of whole-body and regional fat mass are required to inform public health policy and for the measurement and treatment of obesity(1), an epidemic affecting 500 million adults worldwide(2). The Lancet (3) recently highlighted the need to accurately monitor and evaluate obesity interventions as one of the key factors required for the control of this epidemic worldwide.
Dual-energy X-ray absorptiometry (DXA) is an accepted reference method of body composition measurement and has been utilised in both cross-sectional(Reference Kelly, Wilson and Heymsfield4) and longitudinal(Reference Newman, Sun Lee and Visser5) body composition studies. Close agreement has been shown between DXA and the criterion multi-component models in young and older healthy adults(Reference Wang, Deurenberg and Guo6, Reference Clasey, Kanaley and Wideman7). However, DXA is not appropriate in the conduct of large-scale, field-based studies and is deemed unsuitable for some populations sensitised to the use of ionising radiation(1).
Anthropometry and, specifically, the measurement of skinfold thickness and body girths is an indirect, prediction-based method of assessment of body fat that is applicable to large-scale studies(Reference Wang, Thornton and Kolesnik8). In Europe, the age- and sex-specific equations of Durnin & Rahaman(Reference Durnin and Rahaman9) and Durnin & Womersley(Reference Durnin and Womersley10) relating skinfold thickness at four sites (biceps, triceps, subscapular and suprailiac) to percentage body fat (%BF) are widely used. Referencing the body density and thus body fat to that obtained by hydrodensitometry, the Durnin & Womersley(Reference Durnin and Womersley10) equations were constructed from a sample of 481 men and women aged 16–72 years.
And now, 40 years on from Durnin & Rahaman's(Reference Durnin and Rahaman9) original report, the present study re-examines the concept of formulating an equation for calculating body fat from the measurement of skinfold thicknesses. Using DXA as the reference method, the aim of the present study was to construct and validate generalised prediction equations for %BF from anthropometric measures using a robust regression technique in a large sample of adult Irish men and women.
Methods
This study was conducted according to the guidelines laid down in the Declaration of Helsinki and all procedures involving human subjects were approved by the University of Limerick Research Ethics Committee (ULREC 08/07). Written informed consent was obtained from all subjects.
Participants
A total of 1136 healthy adults (518 men and 618 women) aged 18 years or over were recruited from the University of Limerick campus and surrounding community as part of the University of Limerick Body Composition Study (www.ul.ie/bodycompositionstudy). Of these subjects, eight (six men, two women) were of Asian descent, and the remaining 1128 were Caucasian. Subjects were instructed to refrain from exercise for 12 h, to refrain from eating for 3 h and to consume 500 ml of water 1 h before testing. Subjects were also required to empty their bladder immediately before measurement. Height was measured to the nearest 0·1 cm using a stadiometer (Seca) and body mass to the nearest 0·1 kg (Tanita MC-180MA Body Composition Analyzer, Tanita UK Limited).
Dual-energy X-ray absorptiometry
A Lunar iDXA™ scanner with enCORE™ 2007 v.11 software (GE Healthcare) was used to capture total body scans. Daily calibration of the scanner employed a phantom spine containing composites of bone, fat and lean tissue. Participants were positioned on the scanner bed according to the manufacturer's recommendations and instructed to remain as still as possible for the duration of the scan. Where subjects were too wide to fit within the boundary of the scan, the right hand side of the body was scanned and results doubled. This procedure has been validated specifically for the iDXA by Rothney et al. (Reference Rothney, Brychta and Schaefer11). The CV of the iDXA for repeated measures of whole-body composition analysis was 0·6 %.
Anthropometry
Using Harpenden calipers (Assist Creative Resources Limited), skinfold thickness measures were obtained on all subjects at ten sites (forearm, biceps, triceps, subscapular, midaxilla, iliac crest, supraspinale, abdomen, front thigh and medial calf) with an additional chest site measured on men only. Corresponding girth measures were taken at seven body sites (forearm, upper arm, waist, abdomen, hip, mid thigh and calf) on all subjects using a Physiomed tape measure (Physio-med) with an additional chest girth taken on men only. These sites were chosen to represent all body segments and were identified in accordance with the International Society for the Advancement of Kinanthropometry (ISAK) standards(Reference Marfell-Jones, Olds and Stewart12). Exact site location and measurement technique for each anthropometric variable are given in Table 1. In this study, three trained investigators carried out the anthropometric measures. Inter-tester technical error of measurement was < 10 % for skinfold thickness measures and < 2 % for girth measures. Intra-tester technical error of measurement was set at < 5 % for skinfold thickness measures and < 1 % technical error of measurement for girth measures; if technical error of measurements were greater than these values, a third measure was taken and the median value was used for analysis. The existing four site skinfold equations of Durnin & Womersley(Reference Durnin and Womersley10) were applied to the present sample. The four original sites measured by Durnin & Womersley(Reference Durnin and Womersley10) were biceps, triceps, subscapular and suprailiac. In this study, the suprailiac site is replaced by the iliac crest site.
Table 1 Site location and measurement technique for anthropometric measures

* Adapted from Marfell-Jones et al. (Reference Marfell-Jones, Olds and Stewart12).
† Adapted from Heyward & Wagner(Reference Heyward and Wagner14).
Statistical analyses
Statistical analyses were performed using PASW Statistics 18.0 for Windows (SPSS, Inc.) and TIBCO Spotfire S+ 8.1 (TIBCO Software, Inc.). Male and female data were analysed separately in all instances. A Kolgomorov–Smirnov test was conducted to assess whether variables were normally or non-normally distributed. Mean values and standard deviation, median and interquartile range and ranges are reported for descriptive statistics. A Mann–Whitney U test was used, as appropriate, to undertake between-sex comparisons of the dependent variables of interest. Overall, 200 men and 200 women were randomly selected from the total sample for use as a cross-validation sample. Prediction equations were generated on the remaining subjects (validation sample; n 318 men, 418 women).
The relationship between anthropometric measures and %BF was curvilinear, with the exception of the abdomen skinfold and chest and hip girths in men and abdomen, front thigh and medial calf skinfolds and upper arm and abdomen girths in women. All anthropometric variables were therefore log-transformed before regression analysis. Spearman's ρ correlations were used to investigate the relationship between anthropometric measures at each site and also between age, each site and %BF. The anthropometric measure that had the strongest correlation to %BF was retained in all regression investigations. To avoid violating the assumptions of regression analysis, pairs of anthropometric measures that had a higher correlation than either individual site had with %BF were not included in the regression analyses together. Following log-transformation, all anthropometric variables with the exception of front thigh skinfold and forearm, upper arm and calf girths in men and triceps, front thigh skinfold and mid-thigh girth in women were non-normally distributed. Further, initial stepwise linear multiple regression indicated heteroskedacity among the chosen predictor variables. Therefore, quantile regression was used to generate prediction equations for %BF from anthropometric measures in men and women.
%BF measures within sex were compared using Wilcoxon signed-rank tests. Standard error of the estimate (SEE), scatter plots, Spearman's ρ correlations and Bland–Altman(Reference Bland and Altman13) plots were used to investigate agreement and bias between %BF derived from DXA and that derived from anthropometric prediction equations. Besides, 95 % limits of agreement were calculated as the mean of difference between methods ± 1·96 × standard deviation of the difference. Proportional bias was systematically checked for and was indicated when the slope of the Bland–Altman regression line was significantly different from zero.
The prediction equation with the lowest SEE value was chosen as the strongest prediction model. In this analysis, the prediction equation with the lowest SEE also happened to have the highest Spearman's ρ correlation and the narrowest 95 % limits of agreement in both men and women. Bootstrapping re-sampling analysis using 1000 resample sets was carried out on each validation sample. The 95 % CI of the median are reported for the bootstrap analysis. Each prediction equation was then cross-validated on a further 200 subjects.
Statistical significance (two-tailed) was set at P< 0·05 for all analyses.
Results
Descriptive statistics
A total of 518 men and 618 women participated in the study. Descriptive statistics are provided in Table 2. All variables differed between sexes, with women being older (9·7 years) with a higher %BF (12·7 %) and fat tissue mass (4·3 kg) but lower height ( − 0·15 m), mass ( − 17·3 kg) and BMI ( − 4·5 kg/m2) than men (all P< 0·05). In men, 43 % of the total sample were overweight and a further 10 % were obese according to their BMI. These values were 46 and 10 % in the validation sample and 39 and 11 % in the cross-validation sample, respectively. In women, 30 % of the total sample were overweight and a further 9 % were obese. These values were 30 and 10 % in the validation sample and 30 and 8 % in the cross-validation sample, respectively.
Table 2 Descriptive statistics of men (n 518) and women (n 618) (Mean values, standard deviations, medians, ranges and interquartile ranges (IQR))

FTM, fat tissue mass.
* Values are significantly different from those of men (P< 0·05).
Anthropometry
The relationship between %BF and individual anthropometric variables was curvilinear; thus all skinfold thickness and girth measures were log-transformed before regression analysis. Fig. 1 illustrates the midaxilla skinfold in women as an example of the relationship before and after log-transformation. Table 3 illustrates the values for log-transformed anthropometric variables obtained in men and women.

Fig. 1 Relationship of percentage body fat (%BF) and midaxilla skinfold thickness in women (n 618) before and after log-transformation.
Table 3 Log-transformed skinfold thickness (mm) and girth (cm) measures in men (n 518) and women (n 618) (Mean values, standard deviations, medians, ranges and interquartile ranges (IQR))

* Normal distribution.
Generalised prediction equations
Generalised equations to predict %BF were generated for men and women, with age included as an independent variable in addition to anthropometric measures. Skinfold thickness at the midaxilla had the strongest correlation to %BF in both men (r 0·918, P< 0·01) and women (r 0·854, P< 0·01). In men, an equation with age and three skinfold thickness measures (midaxilla, triceps and supraspinale) predicted %BF in the validation group, with a correlation coefficient (r) of 0·95, SEE of 2·6 % and limits of agreement of − 4·9, 5·1 (Table 4). The 95 % CI for the median obtained from bootstrapping analysis were 19·4, 21·5 %. When the prediction equation was applied to the cross-validation sample, there was no difference (P= 0·672) between %BF measured by DXA and that predicted from the skinfold equation, with r 0·95, a SEE of 2·4 % and limits of agreement of − 4·8, 4·6 (Table 4). Similar results were observed when the validation and cross-validation groups were combined; Fig. 2 illustrates the Bland–Altman analysis of agreement between methods in the total group (n 518). In women, an equation with age, abdominal girth and three skinfold thickness measures (biceps, midaxilla and medial calf) predicted %BF in the validation group, with r 0·93, a SEE of 2·7 % and limits of agreement of − 5·3, 5·3 (Table 5). The 95 % CI for the median obtained from bootstrapping analysis were 32·2, 33·8 %. When the equation was applied to the cross-validation sample (n 618), there was no difference (P= 0·176) between %BF measured by DXA and that obtained using the prediction equation. The SEE was 3·5 %, with r 0·93 and limits of agreement were − 6·5, 7·1. When the validation and cross-validation samples were combined, r 0·90, SEE = 3·0 % and limits of agreement were − 5·7, 5·9 (Table 5). Fig. 3 illustrates the Bland–Altman analysis of agreement between methods in the total group (n 618).
Table 4 Generalised regression equation in men aged 18–72 years (n 518) (Mean values, standard deviations and 95 % confidence intervals)

%BF, percentage body fat; DXA, dual-energy X-ray absorptiometry; Δ, difference; r, correlation coefficient; SEE, standard error of the estimate; LoA, limits of agreement; SF, skinfold thickness.

Fig. 2 Bland–Altman analysis of agreement between dual-energy X-ray absorptiometry-measured and skinfold-predicted percentage body fat (%BF) in men (n 518) with mean difference (- - -) and 95 % limits of agreement (…).
Table 5 Generalised regression equation in women aged 18–81 years (n 618) (Mean values, standard deviations and 95 % confidence intervals)

%BF, percentage body fat; DXA, dual-energy X-ray absorptiometry; Δ, difference; r, correlation coefficient; SEE, standard error of the estimate; LoA, limits of agreement; G, girth; SF, skinfold thickness.

Fig. 3 Bland–Altman analysis of agreement between dual-energy X-ray absorptiometry-measured and skinfold-predicted percentage body fat (%BF) in women (n 618) with mean difference (- - -) and 95 % limits of agreement (…).
Though midaxilla skinfold thickness had the highest correlation to %BF in men and women, it is not a common anthropometric measure and may be difficult to record accurately in some subjects. Alternative prediction equations excluding the midaxilla skinfold were also developed and cross-validated. In men, an equation including age, abdominal, subscapular and medial calf skinfolds predicted %BF with an SEE of 5·8 %, r 0·62 and 95 % limits of agreement of − 11·0, 11·6 for the total group (Table 6). In women, an equation including age, abdominal girth and biceps, subscapular and medial calf skinfolds predicted %BF with an SEE of 3·0 %, r 0·92 and 95 % limits of agreement of − 5·7, 6·0 for the total group (Table 7).
Table 6 Alternative generalised regression equation excluding midaxilla skinfold thickness (SF) in men aged 18–72 (n 518) (Mean values, standard deviations and 95 % confidence intervals)

%BF, percentage body fat; DXA, dual-energy X-ray absorptiometry; Δ, difference; r, correlation coefficient; SEE, standard error of the estimate; LoA, limits of agreement.
Table 7 Alternative generalised regression equation excluding midaxilla skinfold thickness (SF) in women aged 18–81 years (n 618) (Mean values, standard deviations and 95 % confidence intervals)

%BF, percentage body fat; DXA, dual-energy X-ray absorptiometry; Δ, difference; r, correlation coefficient; SEE, standard error of the estimate; LoA, limits of agreement.
The prediction equations of Durnin & Womersley(Reference Durnin and Womersley10) were applied to the total sample. Table 7 illustrates the comparison of these equations to DXA-derived %BF in men and women, respectively. Fig. 4 illustrates the Bland–Altman analysis of agreement between DXA-derived %BF and that predicted from the Durnin & Womersley(Reference Durnin and Womersley10) equations in men and women (Table 8).

Fig. 4 Bland–Altman analysis of agreement between percentage body fat (%BF) derived from dual-energy X-ray absorptiometry and that predicted from Durnin and Womersley skinfold equations in (a) men (n 518) and (b) women (n 618) with mean difference (- - -) and 95 % limits of agreement (…).
Table 8 Comparison of Durnin & Womersley (D&W)(Reference Durnin and Womersley10) prediction equations and dual-energy X-ray absorptiometry (DXA)-derived percentage body fat (%BF) in men (n 518) and women (n 618) (Mean values and standard deviations)

Δ, difference; r, correlation coefficient; SEE, standard error of the estimate; LoA, limits of agreement; SF, skinfold thickness.
Σ4SF = sum of four SF measures biceps, triceps, subscapula and iliac crest.
* Values are significantly different from DXA-derived %BF.
Discussion
The purpose of the present study was to construct and validate generalised prediction equations to estimate %BF from anthropometric measures in a large sample of adult men and women (n 1136) ranging widely in age (18–81 years) and %BF (5·1–56·8 %). Cross-validated on an independent subject sample, the data indicate that %BF is accurately predicted from skinfold thickness and girth measures in this group when compared to DXA-derived %BF. Heyward & Wagner(Reference Heyward and Wagner14) recommend that the correlation coefficient (r) for body composition prediction equations should exceed 0·80 and limits of agreement should be within 5 % when compared to the reference method. SEE ≤ 3·0 % between methods is considered ‘very good’ and SEE ≤ 2·5 % is considered ‘excellent’. In men, skinfold thickness measures from three body sites (triceps, midaxilla and supraspinale), combined with age, predicted %BF, with a correlation coefficient (r) of 0·95, SEE of 2·5 % and 95 % limits of agreement of < 5 % for the men (n 518). In women, an equation containing age, abdominal girth and skinfold thickness measures at the biceps, midaxilla and medial calf sites predicted %BF, with r 0·92, SEE of 3·0 % and 95 % limits of agreement of − 5·7, 5·9 for the total subject group (n 618).
The strong correlation of midaxilla skinfold thickness to %BF and the presence of a second predictor variable from the trunk region in both men (supraspinale skinfold thickness) and women (abdominal girth) reflect the deposition of approximately 50 and 45 % of the total fat mass in the trunk segment in men and women, respectively(Reference Leahy, O'Neill and Sohun15). The presence of an abdominal girth in place of a skinfold thickness measure in women may reflect an increased ratio of subcutaneous-to-visceral trunk fat deposition compared to men(Reference Enzi, Gasparo and Biondetti16). The importance of including lower limb skinfold thickness measures in body fat prediction equations has been highlighted previously(Reference Eston, Rowlands and Charlesworth17). However, while medial calf skinfold thickness was found to be a significant predictor of %BF in women in the present study, no lower limb measure was found to be statistically important for inclusion in the final prediction equation in men.
Despite having the strongest correlation to %BF, midaxilla skinfold thickness can be difficult to measure, particularly in women due to clothing restrictions and potential embarrassment to the subject. For this reason, the site is not commonly used to measure %BF and is not included in the ISAK International Standards for Anthropometric Assessment(Reference Marfell-Jones, Olds and Stewart12). %BF prediction equations constructed using only commonly used anthropometric measures suggest that in men, %BF may also be predicted by an equation including age, abdominal, subscapular and medial calf skinfolds, with a ‘poor’ SEE of 5·8 %, moderate correlation of 0·62 and wide 95 % limits of agreement ( − 11·0, 11·6) for the total subject group. Due to the poor accuracy, this equation is not recommended for use in adult men. In women, a prediction equation using abdominal girth and biceps, subscapular and medial calf skinfold thickness has a ‘very good’ SEE of 3·0 % for the total subject group. This equation predicted %BF almost as accurately as that including midaxilla skinfold thickness, with similar correlation coefficient (r 0·92) and 95 % limits of agreement ( − 5·7, 6·0). This alternative equation may be used to accurately predict %BF in women where there is difficulty obtaining the midaxilla skinfold thickness measure or where the investigator is only sufficiently trained in a limited number of anthropometric measures.
The application of the Durnin & Womersley(Reference Durnin and Womersley10) prediction equations to the present sample resulted in a small but statistically significant underestimate of mean %BF values by 1 % in men and 0·8 % in women compared to those obtained using DXA. The SEE values of 3·4 % in men and 4·1 % in women, while higher than those obtained from the equations presented in this paper, are considered ‘good’ and ‘fair’, respectively(Reference Heyward and Wagner14). In the original Durnin & Womersley(Reference Durnin and Womersley10) study, SEE values of 3·5 % for women and 5 % for men were reported, with correlation coefficients ranging from 0·7 to 0·9. Bland–Altman analysis of agreement between methods (Fig. 4) suggests that as subject's %BF increases, the Durnin & Womersley(Reference Durnin and Womersley10) equations are more likely to underestimate %BF when compared to DXA. This bias is more apparent in women than in men and explains the higher SEE value and wider limits of agreement observed in women compared to men. These findings indicate that while Durnin & Womersley's(Reference Durnin and Womersley10) equations are still valid, the equations presented in this paper provide a better estimate of %BF in individuals with very high or very low %BF. The location of the suprailiac skinfold site may account in some part for the difference between DXA-measured %BF and that predicted from the Durnin and Womersley equation. In the present study, the iliac crest skinfold was substituted for the suprailiac site. Durnin & Womersely(Reference Durnin and Womersley10) describe the suprailiac skinfold site as ‘just above the iliac crest in mid-axillary line’. The iliac crest skinfold used in this study is located slightly anteriorally and downwards from this point.
As with all anthropometric prediction models, the equations presented in this paper can only be considered accurate when a carefully standardised protocol is followed by a trained investigator. Anthropometric measures recorded in this study were taken in accordance with ISAK(Reference Marfell-Jones, Olds and Stewart12) standards as follows: all skinfolds were taken on the right hand side of the subjects' body. To ensure maximal accuracy and precision of skinfold thickness measures, sites being measured were carefully landmarked and measures taken with Harpenden spring-loaded calipers calibrated to a force of 10 g/mm2. A double layer of skin and adipose tissue was raised between the left thumb and forefinger. The skinfold calipers were applied 1 cm distally to the investigator's thumb and the thickness recorded to the nearest 1 mm, approximately 2 s after the calipers had been released. A minimum of two measures were taken at each site and the average value used for analysis. It has been shown that skinfold thickness measures taken as little as 1 cm away from a defined ISAK site produce significantly different measurement results at the majority of skinfold sites assessed(Reference Hume and Marfell-Jones18).
Previous studies have used linear regression to derive body composition prediction equations from anthropometric variables(Reference Durnin and Womersley10, Reference Jackson and Pollock19). In the present study, neither anthropometric variables nor %BF were normally distributed. Heteroskedacity was also evident from initial multiple linear regression analysis, and therefore quantile regression was used to construct prediction equations. Quantile regression is a robust regression which has been recommended for use in developing prediction equations for body composition(Reference Heymsfield, Lohman and Wang20). It reduces the influence of outliers on the regression outcome and may explain why there is uniform agreement across the wide range of %BF between DXA and the equations presented here. Additionally, skinfold thickness and girth measures from multiple sites were not summed in the present study, as each site did not contribute an equal amount to the prediction equations.
The subject sample used in this study was a convenience sample recruited from the University of Limerick campus and surrounding community and may not represent the wider Irish population. This is evidenced by the low prevalence of BMI-measured obesity of 10 % in men and 9 % in women. Recent data suggest that the prevalence of obesity in Irish adults is currently 25·8 % in men and 21·3 % in women. To be considered fully representative of the general population, the equations presented here need to be further cross-validated on independent populations.
Conclusion
The anthropometric prediction equations presented here accurately estimate %BF in a large sample of adult men and women ranging widely in age and %BF. The equations of Durnin & Womersley(Reference Durnin and Womersley10) closely predict mean %BF of the total group but appear to become less accurate as %BF increases. The new equations are therefore more appropriate for use in subjects with higher %BF and may be more beneficial in the monitoring and evaluation of obesity interventions.
Acknowledgements
The present study was supported by funding from a University of Limerick Research Grant. The authors declare no conflict of interest. S. L., C. O. and P. J. designed the research; R. S. aided in the recruitment of subjects and administrative tasks. S. L. and C. T. conducted the research; S. L. analysed the data; S. L. and P. J. had primary responsibility for the final content of the manuscript. The authors would like to thank Peter Francis for his contribution to data collection.