Stochastic Geometry and Statistical Applications
Excursion sets of three classes of stable random fields
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 293-318
-
- Article
-
- You have access
- Export citation
Degree sequences of geometric preferential attachment graphs
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 319-330
-
- Article
-
- You have access
- Export citation
On the induced distribution of the shape of the projection of a randomly rotated configuration
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 331-346
-
- Article
-
- You have access
- Export citation
Thinning spatial point processes into Poisson processes
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 347-358
-
- Article
-
- You have access
- Export citation
On variances of partial volumes of the typical cell of a Poisson-Voronoi tessellation and large-dimensional volume degeneracy
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 359-370
-
- Article
-
- You have access
- Export citation
General Applied Probability
Mean reversion for HJMM forward rate models
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 371-391
-
- Article
-
- You have access
- Export citation
Stochastic ordering of classical discrete distributions
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 392-410
-
- Article
-
- You have access
- Export citation
Asymptotic independence for unimodal densities
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 411-432
-
- Article
-
- You have access
- Export citation
Conditionally identically distributed species sampling sequences
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 433-459
-
- Article
-
- You have access
- Export citation
Critical markov branching process limit theorems allowing infinite variance
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 460-488
-
- Article
-
- You have access
- Export citation
Slope distribution in front-back asymmetric stochastic Lagrange time waves
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 489-508
-
- Article
-
- You have access
- Export citation
Aggregation of a random-coefficient ar(1) process with infinite variance and idiosyncratic innovations
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 509-527
-
- Article
-
- You have access
- Export citation
Scaling limits for simple random walks on random ordered graph trees
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 528-558
-
- Article
-
- You have access
- Export citation
Low degree connectivity of ad-hoc networks via percolation
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 559-576
-
- Article
-
- You have access
- Export citation
Asymptotic analysis for personalized Web search
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 577-604
-
- Article
-
- You have access
- Export citation
Front matter
APR volume 42 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
APR volume 42 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

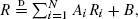 where the
where the