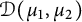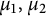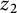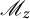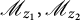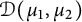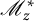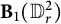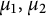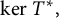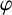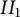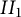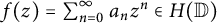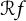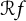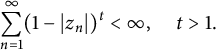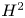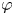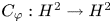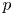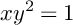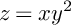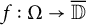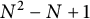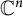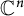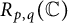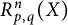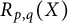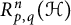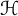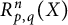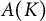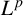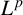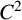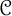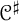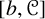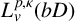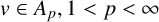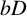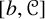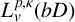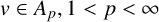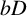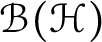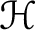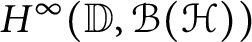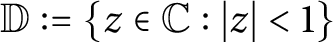84 results in 32Axx
Characterization of continuous homomorphisms on entire slice monogenic functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 17 May 2024, pp. 1-29
-
- Article
- Export citation
Dirichlet-type spaces of the unit bidisc and toral 2-isometries
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CLASS OF SYMBOLS THAT INDUCE BOUNDED COMPOSITION OPERATORS FOR DIRICHLET-TYPE SPACES ON THE DISC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 14 March 2024, pp. 1-6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The degree one Laguerre–Pólya class and the shuffle-word-embedding conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 28 February 2024, pp. 1-8
-
- Article
- Export citation
A characterization of random analytic functions satisfying Blaschke-type conditions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-10
-
- Article
- Export citation
Trigonometric convexity of the multidimensional indicator
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 05 January 2024, pp. 1-16
-
- Article
- Export citation
Linear fractional self-maps of the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 November 2023, pp. 458-468
- Print publication:
- June 2024
-
- Article
- Export citation
ON THE EXCEPTIONAL SET OF TRANSCENDENTAL ENTIRE FUNCTIONS IN SEVERAL VARIABLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 October 2023, pp. 1-8
-
- Article
- Export citation
Schatten class composition operators on the Hardy space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1-14
-
- Article
- Export citation
Uncertainty principles in holomorphic function spaces on the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 122-136
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A logarithmic lower bound for the second Bohr radius
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 27 June 2023, pp. 90-93
- Print publication:
- March 2024
-
- Article
- Export citation
ERRATUM TO “NON-UNIFORMLY FLAT AFFINE ALGEBRAIC HYPERSURFACES”
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 252 / December 2023
- Published online by Cambridge University Press:
- 06 June 2023, pp. 985-989
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
Determining sets for holomorphic functions on the symmetrized bidisk
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 984-996
- Print publication:
- September 2023
-
- Article
- Export citation
A note on cyclic vectors in Dirichlet-type spaces in the unit ball of
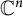 ${\mathbb C}^n$
${\mathbb C}^n$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 January 2023, pp. 886-902
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Estimates for generalized Bohr radii in one and higher dimensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 04 November 2022, pp. 682-699
- Print publication:
- June 2023
-
- Article
- Export citation
A polynomial approximation result for free Herglotz–Agler functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 October 2022, pp. 665-678
- Print publication:
- June 2023
-
- Article
- Export citation
Some remarks on approximation in several complex variables
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 October 2022, pp. 643-653
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $\boldsymbol {L^{p}}$ REGULARITY OF THE SZEGÖ PROJECTION ON THE SYMMETRISED POLYDISC
$\boldsymbol {L^{p}}$ REGULARITY OF THE SZEGÖ PROJECTION ON THE SYMMETRISED POLYDISC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 12 May 2022, pp. 481-490
- Print publication:
- December 2022
-
- Article
- Export citation
BOUNDEDNESS AND COMPACTNESS OF CAUCHY-TYPE INTEGRAL COMMUTATOR ON WEIGHTED MORREY SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 08 March 2022, pp. 36-56
- Print publication:
- August 2022
-
- Article
- Export citation
Operator valued analogues of multidimensional Bohr’s inequality
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 1020-1035
- Print publication:
- December 2022
-
- Article
- Export citation