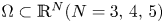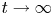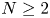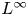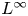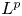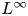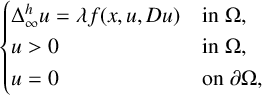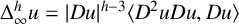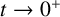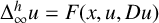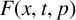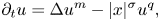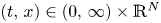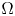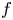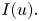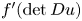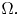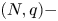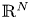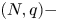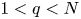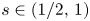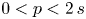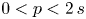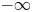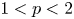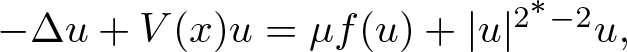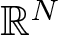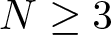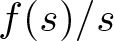108 results in 35Cxx
On a localization-in-frequency approach for a class of elliptic problems with singular boundary data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1-35
-
- Article
- Export citation
Diffuse-interface approximation and weak–strong uniqueness of anisotropic mean curvature flow
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1-61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global boundedness and large time behaviour in a higher-dimensional quasilinear chemotaxis system with consumption of chemoattractant
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 April 2024, pp. 1-26
-
- Article
- Export citation
Uniqueness and Hyers–Ulam’s stability for a fractional nonlinear partial integro-differential equation with variable coefficients and a mixed boundary condition
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized second order vectorial ∞-eigenvalue problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 March 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
VISCOSITY SOLUTIONS TO THE INFINITY LAPLACIAN EQUATION WITH SINGULAR NONLINEAR TERMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 March 2024, pp. 1-30
-
- Article
- Export citation
Eternal solutions to a porous medium equation with strong non-homogeneous absorption. Part I: radially non-increasing profiles
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 March 2024, pp. 1-22
-
- Article
- Export citation
Derivation and travelling wave analysis of phenotype-structured haptotaxis models of cancer invasion
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 27 February 2024, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Adhesion and volume filling in one-dimensional population dynamics under Dirichlet boundary condition
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 January 2024, pp. 1-49
-
- Article
- Export citation
Solvability of Hessian quotient equations in exterior domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 December 2023, pp. 1-31
-
- Article
- Export citation
Analysis and numerical simulations of travelling waves due to plant–soil negative feedback
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 07 December 2023, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence of renormalized solutions to fully anisotropic and inhomogeneous elliptic problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 31 October 2023, pp. 1-37
-
- Article
- Export citation
Generic ill-posedness of the energy–momentum equations and differential inclusions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 September 2023, pp. 1-26
-
- Article
- Export citation
Generalised solution to a 2D parabolic-parabolic chemotaxis system for urban crime: Global existence and large-time behaviour
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 25 September 2023, pp. 409-429
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a class of special Euler–Lagrange equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 21 September 2023, pp. 1-24
-
- Article
- Export citation
Periodic and solitary waves in a Korteweg–de Vries equation with delay
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 September 2023, pp. 1-23
-
- Article
- Export citation
A weighted Trudinger–Moser inequalities and applications to some weighted $(N,q)-$
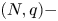 Laplacian equation in $\mathbb {R}^N$
Laplacian equation in $\mathbb {R}^N$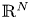 with new exponential growth conditions
with new exponential growth conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 September 2023, pp. 1-52
-
- Article
- Export citation
On large solutions for fractional Hamilton–Jacobi equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 July 2023, pp. 1-23
-
- Article
- Export citation
A non-periodic indefinite variational problem in ℝN with critical exponent
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 579-612
-
- Article
- Export citation
Interface behaviour of the slow diffusion equation with strong absorption: Intermediate-asymptotic properties
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 14 June 2023, pp. 1099-1132
-
- Article
-
- You have access
- Open access
- HTML
- Export citation