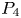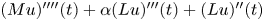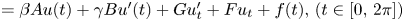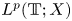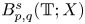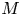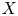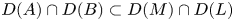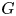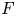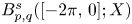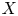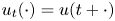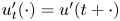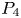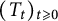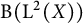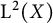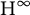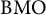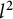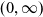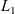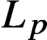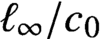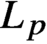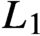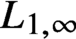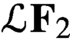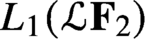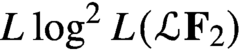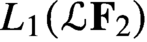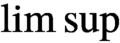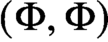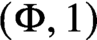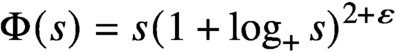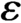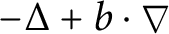58 results in 47Dxx
Propagation of anisotropic Gabor wave front sets
- Part of
- Partial differential equations on manifolds; differential operators
- Distributions, generalized functions, distribution spaces
- Integral, integro-differential, and pseudodifferential operators
- General quantum mechanics and problems of quantization
- Groups and semigroups of linear operators, their generalizations and applications
- Partial differential equations
- Miscellaneous topics - Partial differential equations
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-25
-
- Article
- Export citation
EVENTUAL POSITIVITY AND ASYMPTOTIC BEHAVIOUR FOR HIGHER-ORDER EVOLUTION EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 26 October 2023, pp. 165-167
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
Periodic solutions of four-order degenerate differential equations with finite delay in vector-valued function spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 September 2023, pp. 1-18
-
- Article
- Export citation
Estimates for evolutionary partial differential equations in classical function spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 01 September 2023, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SPECTRAL MULTIPLIER THEOREMS FOR ABSTRACT DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 343-344
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
TROTTER–KATO PRODUCT FORMULA AND AN APPROXIMATION FORMULA FOR A PROPAGATOR IN SYMMETRIC OPERATOR IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 173-174
- Print publication:
- August 2023
-
- Article
-
- You have access
- HTML
- Export citation
Overcoming the timescale barrier in molecular dynamics: Transfer operators, variational principles and machine learning
- Part of
-
- Journal:
- Acta Numerica / Volume 32 / May 2023
- Published online by Cambridge University Press:
- 11 May 2023, pp. 517-673
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- Export citation
Local and global existence and uniqueness of solution for abstract differential equations with state-dependent argument
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 26 April 2023, pp. 305-345
-
- Article
- Export citation
Dilations of Markovian semigroups of measurable Schur multipliers
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 05 April 2023, pp. 774-797
- Print publication:
- June 2024
-
- Article
- Export citation
Polynomial stability of a piezoelectric beam with magnetic effect and a boundary dissipation of the fractional derivative type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 05 April 2023, pp. 23-53
-
- Article
- Export citation
Matrix calculations for moments of Markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 126-150
- Print publication:
- March 2023
-
- Article
- Export citation
Bowen–Walters expansiveness for semigroups of linear operators
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 18 April 2022, pp. 1942-1951
- Print publication:
- June 2023
-
- Article
- Export citation
REPRESENTING STRUCTURED SEMIGROUPS ON ÉTALE GROUPOID BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 April 2022, pp. 1-49
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sampling and interpolation for the discrete Hilbert and Kak–Hilbert transforms
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 07 March 2022, pp. 395-410
- Print publication:
- June 2023
-
- Article
- Export citation
The fragmentation equation with size diffusion: Well posedness and long-term behaviour
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 16 December 2021, pp. 1083-1116
-
- Article
- Export citation
TRANSITION DENSITIES OF SUBORDINATORS OF POSITIVE ORDER
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 22 October 2021, pp. 1119-1179
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FUNCTIONAL CALCULI FOR SECTORIAL OPERATORS AND RELATED FUNCTION THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 04 October 2021, pp. 1383-1463
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wold decomposition on odometer semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 13 July 2021, pp. 738-755
- Print publication:
- June 2022
-
- Article
- Export citation
Noncommutative strong maximals and almost uniform convergence in several directions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 November 2020, e57
-
- Article
-
- You have access
- Open access
- Export citation
Regularity theory of Kolmogorov operator revisited
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 24 August 2020, pp. 725-736
- Print publication:
- December 2021
-
- Article
- Export citation