52 results in 65Lxx
The aromatic bicomplex for the description of divergence-free aromatic forms and volume-preserving integrators
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 08 August 2023, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Control of port-Hamiltonian differential-algebraic systems and applications
- Part of
-
- Journal:
- Acta Numerica / Volume 32 / May 2023
- Published online by Cambridge University Press:
- 11 May 2023, pp. 395-515
- Print publication:
- May 2023
-
- Article
- Export citation
A COMPARISON OF EXPLICIT RUNGE–KUTTA METHODS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 3 / July 2022
- Published online by Cambridge University Press:
- 19 October 2022, pp. 227-249
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HIGH ORDER EXPLICIT SECOND DERIVATIVE METHODS WITH STRONG STABILITY PROPERTIES BASED ON TAYLOR SERIES CONDITIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 3 / July 2022
- Published online by Cambridge University Press:
- 23 September 2022, pp. 264-291
-
- Article
- Export citation
EXPLICIT NORDSIECK SECOND DERIVATIVE GENERAL LINEAR METHODS FOR ODES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 69-88
-
- Article
- Export citation
LINEARLY IMPLICIT ENERGY-PRESERVING FOURIER PSEUDOSPECTRAL SCHEMES FOR THE COMPLEX MODIFIED KORTEWEG–DE VRIES EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 3 / July 2020
- Published online by Cambridge University Press:
- 12 January 2021, pp. 256-273
-
- Article
- Export citation
Estimates for sums and gaps of eigenvalues of Laplacians on measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 June 2020, pp. 842-861
- Print publication:
- April 2021
-
- Article
- Export citation
Time adaptive numerical solution of a highly non-linear degenerate cross-diffusion system arising in multi-species biofilm modelling
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 10 September 2018, pp. 1035-1061
-
- Article
-
- You have access
- Export citation
An Adaptive Semi-Lagrangian Level-Set Method for Convection-Diffusion Equations on Evolving Interfaces
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1364-1382
- Print publication:
- December 2017
-
- Article
- Export citation
Analysis of Mathematics and Numerical Pattern Formation in Superdiffusive Fractional Multicomponent System
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1438-1460
- Print publication:
- December 2017
-
- Article
- Export citation
Uniform convergence over time of a nested particle filtering scheme for recursive parameter estimation in state-space Markov models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 17 November 2017, pp. 1170-1200
- Print publication:
- December 2017
-
- Article
- Export citation
Convergence Analysis for a Three-Level Finite Difference Scheme of a Second Order Nonlinear ODE Blow-Up Problem
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 679-696
- Print publication:
- November 2017
-
- Article
- Export citation
A Convergence Analysis of the MINRES Method for Some Hermitian Indefinite Systems
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 827-836
- Print publication:
- November 2017
-
- Article
- Export citation
A Finite Difference Method for Boundary Value Problems of a Caputo Fractional Differential Equation
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 752-766
- Print publication:
- November 2017
-
- Article
- Export citation
Detached Eddy Simulation of Complex Separation Flows Over a Modern Fighter Model at High Angle of Attack
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 31 October 2017, pp. 1309-1332
- Print publication:
- November 2017
-
- Article
- Export citation
A NEW MINIMIZATION PRINCIPLE FOR THE POISSON EQUATION LEADING TO A FLEXIBLE FINITE ELEMENT APPROACH
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 03 October 2017, pp. 232-239
-
- Article
-
- You have access
- Export citation
Computable Error Estimates for a Nonsymmetric Eigenvalue Problem
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 07 September 2017, pp. 583-602
- Print publication:
- August 2017
-
- Article
- Export citation
A High-Order Method for Weakly Compressible Flows
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 4 / October 2017
- Published online by Cambridge University Press:
- 28 July 2017, pp. 1150-1174
- Print publication:
- October 2017
-
- Article
- Export citation
An Essential Extension of the Finite-Energy Condition for Extended Runge-Kutta-Nyström Integrators when Applied to Nonlinear Wave Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 06 July 2017, pp. 742-764
- Print publication:
- September 2017
-
- Article
- Export citation
A Domain Decomposition Based Spectral Collocation Method for Lane-Emden Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 2 / August 2017
- Published online by Cambridge University Press:
- 21 June 2017, pp. 542-571
- Print publication:
- August 2017
-
- Article
- Export citation



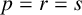
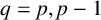
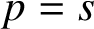
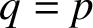
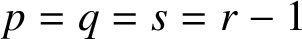
 , where
, where 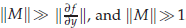 . The highly oscillatory system is due to the semi-discretisation of conservative, or dissipative, nonlinear wave equations. The structure of such a matrix
. The highly oscillatory system is due to the semi-discretisation of conservative, or dissipative, nonlinear wave equations. The structure of such a matrix 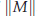 . Since stepsizes are not restricted by frequencies of
. Since stepsizes are not restricted by frequencies of 