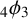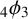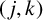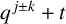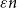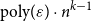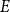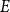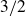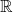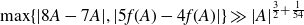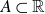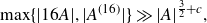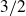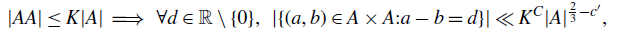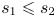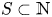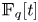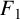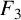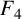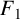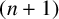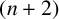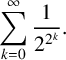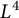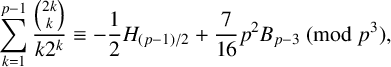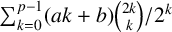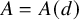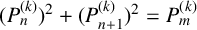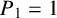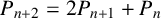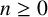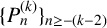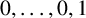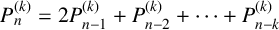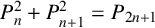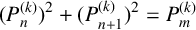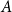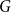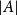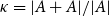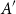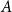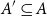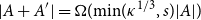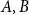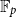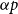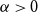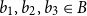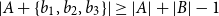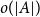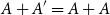292 results in 11Bxx
THEOREM OF WARD ON SYMMETRIES OF ELLIPTIC NETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 October 2024, pp. 1-14
-
- Article
-
- You have access
- HTML
- Export citation
Supercongruences involving Motzkin numbers and central trinomial coefficients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 October 2024, pp. 1-25
-
- Article
-
- You have access
- HTML
- Export citation
A q-SUPERCONGRUENCE ARISING FROM ANDREWS’
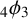 $_4\phi _3$ IDENTITY
$_4\phi _3$ IDENTITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 29 August 2024, pp. 1-5
-
- Article
-
- You have access
- HTML
- Export citation
MULTIPLICATIVE FUNCTIONS k-ADDITIVE ON GENERALISED OCTAGONAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-11
-
- Article
-
- You have access
- HTML
- Export citation
Maximizing weighted sums of binomial coefficients using generalized continued fractions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
CHARACTERISTIC POLYNOMIALS OF THE MATRICES WITH
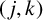 $(\,j,k)$-ENTRY
$(\,j,k)$-ENTRY 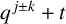 $q^{\,j\pm k}+t$
$q^{\,j\pm k}+t$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-10
-
- Article
-
- You have access
- HTML
- Export citation
A generalisation of Varnavides’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 29 May 2024, pp. 1-5
-
- Article
-
- You have access
- HTML
- Export citation
A better than
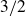 $3/2$ exponent for iterated sums and products over
$3/2$ exponent for iterated sums and products over 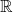 $\mathbb R$
$\mathbb R$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
A solution to the Erdős–Sárközy–Sós problem on asymptotic Sidon bases of order 3
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1418-1432
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NEW CONGRUENCES FOR THE TRUNCATED APPELL SERIES
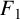 $F_1$
$F_1$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1-8
-
- Article
-
- You have access
- HTML
- Export citation
APPROXIMATION OF IRRATIONAL NUMBERS BY PAIRS OF INTEGERS FROM A LARGE SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE SUMMED PAPERFOLDING SEQUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 25 March 2024, pp. 189-198
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
Almost sure convergence of the
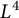 $L^4$ norm of Littlewood polynomials
$L^4$ norm of Littlewood polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 872-885
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
ON SOME CONGRUENCES INVOLVING CENTRAL BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
Proof of some conjectural congruences involving Apéry and Apéry-like numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 508-527
-
- Article
-
- You have access
- HTML
- Export citation
Relative rank and regularization
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 March 2024, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DIOPHANTINE EQUATION
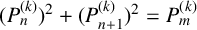 $(P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m$
$(P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 211-215
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
Linear independence of series related to the Thue–Morse sequence along powers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 822-832
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
ENERGY BOUNDS FOR MODULAR ROOTS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Small subsets with large sumset: Beyond the Cauchy–Davenport bound
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 21 February 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation