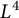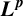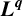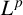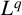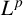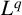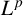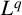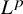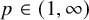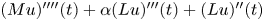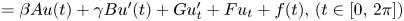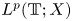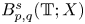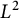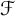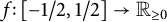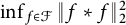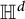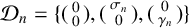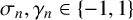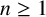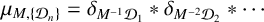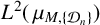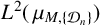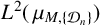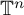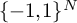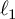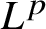88 results in 42Axx
A mathematical theory of super-resolution and two-point resolution
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 21 October 2024, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A unified characterization of convolution coefficients in nonlocal differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-19
-
- Article
-
- You have access
- HTML
- Export citation
Almost sure convergence of the
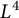 $L^4$ norm of Littlewood polynomials
$L^4$ norm of Littlewood polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 872-885
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Tree structure of spectra of spectral Moran measures with consecutive digits
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 593-610
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
QUALITATIVE UNCERTAINTY PRINCIPLE ON CERTAIN LIE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 289-307
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
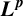 $\boldsymbol {L}^{\boldsymbol {p}}$–
$\boldsymbol {L}^{\boldsymbol {p}}$–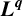 $\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
$\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 18 October 2023, pp. 375-395
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
On a multi-parameter variant of the Bellow–Furstenberg problem
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 September 2023, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Periodic solutions of four-order degenerate differential equations with finite delay in vector-valued function spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 September 2023, pp. 1-18
-
- Article
-
- You have access
- HTML
- Export citation
Remarks on countable subadditivity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 23 August 2023, pp. 1504-1517
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
An optimal
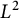 $L^2$ autoconvolution inequality
$L^2$ autoconvolution inequality
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 July 2023, pp. 108-121
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SPECTRAL MULTIPLIER THEOREMS FOR ABSTRACT DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 343-344
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
The Lp convergence of Fourier series on triangular domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 453-474
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Logan’s problem for Jacobi transforms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 April 2023, pp. 915-945
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Abstract almost periodicity for group actions on uniform topological spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 798-829
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NONSPECTRAL PROBLEM FOR PLANAR MORAN–SIERPINSKI MEASURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 11 January 2023, pp. 308-319
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
Brownian bridge expansions for Lévy area approximations and particular values of the Riemann zeta function
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 03 November 2022, pp. 370-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Divergence of mock Fourier series for spectral measures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 17 October 2022, pp. 1818-1832
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
VARIANTS OF A MULTIPLIER THEOREM OF KISLYAKOV
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 01 September 2022, pp. 347-377
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation
Bounds for spectral projectors on tori
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 12 May 2022, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THREE-DIMENSIONAL ANALYTICAL SOLUTION OF THE ADVECTION-DIFFUSION EQUATION FOR AIR POLLUTION DISPERSION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 26 April 2022, pp. 40-53
-
- Article
- Export citation