No CrossRef data available.
Article contents
A NONSPECTRAL PROBLEM FOR PLANAR MORAN–SIERPINSKI MEASURES
Published online by Cambridge University Press: 11 January 2023
Abstract
Let 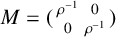 $M=(\begin {smallmatrix}\rho ^{-1} & 0 \\0 & \rho ^{-1} \\\end {smallmatrix})$ be an expanding real matrix with
$M=(\begin {smallmatrix}\rho ^{-1} & 0 \\0 & \rho ^{-1} \\\end {smallmatrix})$ be an expanding real matrix with 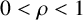 $0<\rho <1$, and let
$0<\rho <1$, and let 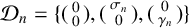 ${\mathcal D}_n=\{(\begin {smallmatrix} 0\\ 0 \end {smallmatrix}),(\begin {smallmatrix} \sigma _n\\ 0 \end {smallmatrix}),(\begin {smallmatrix} 0\\ \gamma _n \end {smallmatrix})\}$ be digit sets with
${\mathcal D}_n=\{(\begin {smallmatrix} 0\\ 0 \end {smallmatrix}),(\begin {smallmatrix} \sigma _n\\ 0 \end {smallmatrix}),(\begin {smallmatrix} 0\\ \gamma _n \end {smallmatrix})\}$ be digit sets with 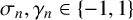 $\sigma _n,\gamma _n\in \{-1,1\}$ for each
$\sigma _n,\gamma _n\in \{-1,1\}$ for each 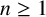 $n\ge 1$. Then the infinite convolution
$n\ge 1$. Then the infinite convolution 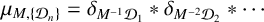 $$ \begin{align*}\mu_{M,\{{\mathcal D}_n\}}=\delta_{M^{-1}{\mathcal D}_1}\ast\delta_{M^{-2}{\mathcal D}_2}\ast\cdots\end{align*} $$
$$ \begin{align*}\mu_{M,\{{\mathcal D}_n\}}=\delta_{M^{-1}{\mathcal D}_1}\ast\delta_{M^{-2}{\mathcal D}_2}\ast\cdots\end{align*} $$
is called a Moran–Sierpinski measure. We give a necessary and sufficient condition for 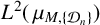 $L^2(\,\mu _{M,\{{\mathcal D}_n\}})$ to admit an infinite orthogonal set of exponential functions. Furthermore, we give the exact cardinality of orthogonal exponential functions in
$L^2(\,\mu _{M,\{{\mathcal D}_n\}})$ to admit an infinite orthogonal set of exponential functions. Furthermore, we give the exact cardinality of orthogonal exponential functions in 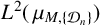 $L^2(\,\mu _{M,\{{\mathcal D}_n\}})$ when
$L^2(\,\mu _{M,\{{\mathcal D}_n\}})$ when 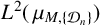 $L^2(\,\mu _{M,\{{\mathcal D}_n\}})$ does not admit any infinite orthogonal set of exponential functions based on whether
$L^2(\,\mu _{M,\{{\mathcal D}_n\}})$ does not admit any infinite orthogonal set of exponential functions based on whether 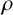 $\rho $ is a trinomial number or not.
$\rho $ is a trinomial number or not.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 108 , Issue 2 , October 2023 , pp. 308 - 319
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This work was supported by the National Natural Science Foundation of China, Grant no. 11971194.



