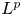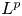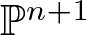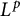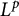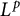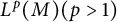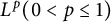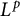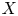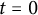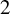99 results in 58Jxx
Lp positivity preservation and self-adjointness of Schrödinger operators on incomplete Riemannian manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Projectively and affinely invariant PDEs on hypersurfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1-26
-
- Article
- Export citation
Propagation of anisotropic Gabor wave front sets
- Part of
- Partial differential equations on manifolds; differential operators
- Distributions, generalized functions, distribution spaces
- Integral, integro-differential, and pseudodifferential operators
- General quantum mechanics and problems of quantization
- Groups and semigroups of linear operators, their generalizations and applications
- Partial differential equations
- Miscellaneous topics - Partial differential equations
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-25
-
- Article
- Export citation
Index estimates of compact hypersurfaces in smooth metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1-19
-
- Article
- Export citation
On Calderon's problem for the connection Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 January 2024, pp. 1-26
-
- Article
- Export citation
Anisotropic flow, entropy, and
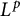 $L^p$-Minkowski problem
$L^p$-Minkowski problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differential Harnack estimates for a weighted nonlinear parabolic equation under a super Perelman–Ricci flow and implications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prescribing nearly constant curvatures on balls
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1-36
-
- Article
- Export citation
A universal inequality for Neumann eigenvalues of the Laplacian on a convex domain in Euclidean space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 19 September 2023, pp. 222-226
- Print publication:
- March 2024
-
- Article
- Export citation
Gaussian fluctuations in the equipartition principle for Wigner matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 August 2023, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTRACTING FEATURES FROM EIGENFUNCTIONS: HIGHER CHEEGER CONSTANTS AND SPARSE EIGENBASIS APPROXIMATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 511-512
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
The aromatic bicomplex for the description of divergence-free aromatic forms and volume-preserving integrators
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 08 August 2023, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative regular Riemann–Hilbert correspondence II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 15 June 2023, pp. 1413-1465
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniqueness of
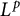 $L^p$ subsolutions to the heat equation on Finsler measure spaces
$L^p$ subsolutions to the heat equation on Finsler measure spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 166-175
- Print publication:
- March 2024
-
- Article
- Export citation
Superscars for arithmetic point scatters II
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 May 2023, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BCOV invariant and blow-up
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 28 March 2023, pp. 780-829
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REILLY-TYPE UPPER BOUNDS FOR THE p-STEKLOV PROBLEM ON SUBMANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 28 February 2023, pp. 492-503
- Print publication:
- December 2023
-
- Article
- Export citation
Heat kernel asymptotics for real powers of Laplacians
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 January 2023, pp. 367-393
- Print publication:
- April 2024
-
- Article
- Export citation
Equivariant Brill–Noether theory for elliptic operators and superrigidity of J-holomorphic maps
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 16 January 2023, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analytic torsion for log-Enriques surfaces and Borcherds product
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation