23 results in 49Lxx
On a mixed singular/switching control problem with multiple regimes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 22 August 2022, pp. 743-782
- Print publication:
- September 2022
-
- Article
- Export citation
Optimal entry and consumption under habit formation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 10 March 2022, pp. 433-459
- Print publication:
- June 2022
-
- Article
- Export citation
Exponential ergodicity and steady-state approximations for a class of markov processes under fast regime switching
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 March 2021, pp. 1-29
- Print publication:
- March 2021
-
- Article
- Export citation
Ergodic control of diffusions with random intervention times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 1-21
- Print publication:
- March 2021
-
- Article
- Export citation
Two-player zero-sum stochastic differential games with random horizon
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 November 2019, pp. 1209-1235
- Print publication:
- December 2019
-
- Article
- Export citation
MINIMIZING THE PROBABILITY OF LIFETIME RUIN: TWO RISKLESS ASSETS WITH TRANSACTION COSTS
- Part of
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 49 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 July 2019, pp. 847-883
- Print publication:
- September 2019
-
- Article
- Export citation
On an optimal extraction problem with regime switching
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 671-705
- Print publication:
- September 2018
-
- Article
- Export citation
An optimal consumption and investment problem with partial information
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 131-153
- Print publication:
- March 2018
-
- Article
-
- You have access
- Export citation
Optimal dividend strategies for two collaborating insurance companies
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 26 June 2017, pp. 515-548
- Print publication:
- June 2017
-
- Article
- Export citation
Optimal financing and dividend distribution in a general diffusion model with regime switching
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 406-422
- Print publication:
- June 2016
-
- Article
- Export citation
A convergence result for the ergodic problem for Hamilton–Jacobi equations with Neumann-type boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 225-242
- Print publication:
- April 2016
-
- Article
- Export citation
CPDO WITH FINITE TERMINATION: MAXIMAL RETURN UNDER CASH-IN AND CASH-OUT CONDITIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 57 / Issue 3 / January 2016
- Published online by Cambridge University Press:
- 10 February 2016, pp. 207-221
-
- Article
-
- You have access
- Export citation
Partially informed investors: hedging in an incomplete market with default
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 718-735
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
On the asymptotic optimality of greedy index heuristics for multi-action restless bandits
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 652-667
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Monotone Policies and Indexability for Bidirectional Restless Bandits
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 51-85
- Print publication:
- March 2013
-
- Article
-
- You have access
- Export citation
Approximation of bounds on mixed-level orthogonal arrays
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 399-421
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Superlinear elliptic equation for fully nonlinear operators without growth restrictions for the data
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 125-141
-
- Article
-
- You have access
- Export citation
Some indexable families of restless bandit problems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 643-672
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Spinning plates and squad systems: policies for bi-directional restless bandits
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 95-115
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Stopping at the maximum of geometric Brownian motion when signals are received
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 826-838
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation



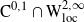
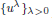 to a solution of the ergodic problem as λ → 0, and give a representation formula for the limit function via the Mather measures and Peierls function. As an interesting by-product, we introduce Mather measures associated with Hamilton–Jacobi equations with the Neumann-type boundary conditions. These results are variants of the main results in a recent paper by Davini
to a solution of the ergodic problem as λ → 0, and give a representation formula for the limit function via the Mather measures and Peierls function. As an interesting by-product, we introduce Mather measures associated with Hamilton–Jacobi equations with the Neumann-type boundary conditions. These results are variants of the main results in a recent paper by Davini 