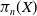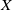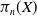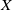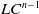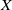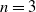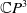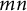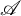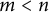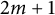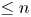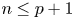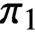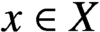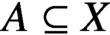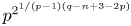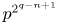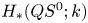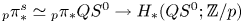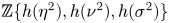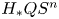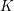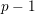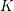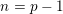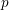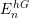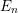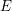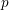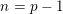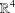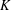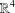19 results in 55Qxx
Moore’s conjecture for connected sums
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 04 December 2023, pp. 516-531
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A natural pseudometric on homotopy groups of metric spaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 08 November 2023, pp. 162-174
- Print publication:
- January 2024
-
- Article
- Export citation
Some asymptotic formulae for torsion in homotopy groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 29 June 2023, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The affirmative answer to Singer's conjecture on the algebraic transfer of rank four
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 23 August 2022, pp. 1529-1542
- Print publication:
- October 2023
-
- Article
- Export citation
Homotopy commutativity in Hermitian symmetric spaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 18 April 2022, pp. 746-752
- Print publication:
- September 2022
-
- Article
- Export citation
Decomposition of topological Azumaya algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 506-524
- Print publication:
- June 2022
-
- Article
- Export citation
Galois symmetries of knot spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 997-1021
- Print publication:
- May 2021
-
- Article
- Export citation
NOTE ON SAMELSON PRODUCTS IN EXCEPTIONAL LIE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 24 November 2020, pp. 741-752
- Print publication:
- September 2021
-
- Article
- Export citation
INFINITARY COMMUTATIVITY AND ABELIANIZATION IN FUNDAMENTAL GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 23 November 2020, pp. 289-311
- Print publication:
- June 2022
-
- Article
- Export citation
Bounding size of homotopy groups of Spheres
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 05 November 2020, pp. 1100-1105
-
- Article
- Export citation
Freudenthal's theorem and spherical classes in H*QS0
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 20 December 2019, pp. 323-341
-
- Article
- Export citation
Higher homotopy associativity in the Harris decomposition of Lie groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 11 September 2019, pp. 2982-3000
- Print publication:
- December 2020
-
- Article
- Export citation
Some results on extension of maps and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1465-1472
- Print publication:
- December 2019
-
- Article
- Export citation
Spaces which Invert Weak Homotopy Equivalences
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 553-558
-
- Article
- Export citation
Algebraic EHP Sequences Revisited
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 625-640
-
- Article
- Export citation
Leibniz Rule on Higher Pages of Unstable Spectral Sequences
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 01 February 2018, pp. 265-282
-
- Article
- Export citation
Picard groups of higher real
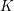 $K$-theory spectra at height
$K$-theory spectra at height 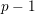 $p-1$
$p-1$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 1820-1854
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
EVERY COUNTABLE GROUP IS THE FUNDAMENTAL GROUP OF SOME COMPACT SUBSPACE OF
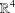 $\mathbb{R}^{4}$
$\mathbb{R}^{4}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 17 April 2015, pp. 145-148
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
A fundamental group topology
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 3 / December 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 416-420
- Print publication:
- December 1984
-
- Article
-
- You have access
- Export citation